Eigen::LeastSquareDiagonalPreconditioner< _Scalar > Class Template Reference

Jacobi preconditioner for LeastSquaresConjugateGradient. More...

#include <BasicPreconditioners.h>

Inheritance diagram for Eigen::LeastSquareDiagonalPreconditioner< _Scalar >:

Collaboration diagram for Eigen::LeastSquareDiagonalPreconditioner< _Scalar >:

List of all members.

Public Member Functions
	LeastSquareDiagonalPreconditioner ()
template<typename MatType >
	LeastSquareDiagonalPreconditioner (const MatType &mat)
template<typename MatType >
LeastSquareDiagonalPreconditioner &	analyzePattern (const MatType &)
template<typename MatType >
LeastSquareDiagonalPreconditioner &	factorize (const MatType &mat)
template<typename MatType >
LeastSquareDiagonalPreconditioner &	compute (const MatType &mat)
ComputationInfo	info ()
Private Types
typedef _Scalar	Scalar
typedef NumTraits< Scalar >::Real	RealScalar
typedef DiagonalPreconditioner < _Scalar >	Base

---

Detailed Description

template<typename _Scalar>
class Eigen::LeastSquareDiagonalPreconditioner< _Scalar >

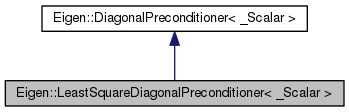
Jacobi preconditioner for LeastSquaresConjugateGradient.

This class allows to approximately solve for A' A x = A' b problems assuming A' A is a diagonal matrix. In other words, this preconditioner neglects all off diagonal entries and, in Eigen's language, solves for:

    (A.adjoint() * A).diagonal().asDiagonal() * x = b

Template Parameters:

_Scalar

the type of the scalar.

The diagonal entries are pre-inverted and stored into a dense vector.

See also:

class LeastSquaresConjugateGradient, class DiagonalPreconditioner

Definition at line 128 of file BasicPreconditioners.h.

---

Member Typedef Documentation

template<typename _Scalar >

typedef DiagonalPreconditioner<_Scalar> Eigen::LeastSquareDiagonalPreconditioner< _Scalar >::Base [private]

Definition at line 132 of file BasicPreconditioners.h.

template<typename _Scalar >

typedef NumTraits<Scalar>::Real Eigen::LeastSquareDiagonalPreconditioner< _Scalar >::RealScalar [private]

Definition at line 131 of file BasicPreconditioners.h.

template<typename _Scalar >

typedef _Scalar Eigen::LeastSquareDiagonalPreconditioner< _Scalar >::Scalar [private]

Reimplemented from Eigen::DiagonalPreconditioner< _Scalar >.

Definition at line 130 of file BasicPreconditioners.h.

---

Constructor & Destructor Documentation

template<typename _Scalar >

Eigen::LeastSquareDiagonalPreconditioner< _Scalar >::LeastSquareDiagonalPreconditioner

(

)

[inline]

Definition at line 136 of file BasicPreconditioners.h.

: Base() {}

template<typename _Scalar >

template<typename MatType >

Eigen::LeastSquareDiagonalPreconditioner< _Scalar >::LeastSquareDiagonalPreconditioner

(

const MatType &

mat

)

[inline, explicit]

Definition at line 139 of file BasicPreconditioners.h.

                                                                   : Base()
    {
      compute(mat);
    }

---

Member Function Documentation

template<typename _Scalar >

template<typename MatType >

LeastSquareDiagonalPreconditioner& Eigen::LeastSquareDiagonalPreconditioner< _Scalar >::analyzePattern

(

const MatType &

)

[inline]

Reimplemented from Eigen::DiagonalPreconditioner< _Scalar >.

Definition at line 145 of file BasicPreconditioners.h.

    {
      return *this;
    }

template<typename _Scalar >

template<typename MatType >

LeastSquareDiagonalPreconditioner& Eigen::LeastSquareDiagonalPreconditioner< _Scalar >::compute

(

const MatType &

mat

)

[inline]

Reimplemented from Eigen::DiagonalPreconditioner< _Scalar >.

Definition at line 168 of file BasicPreconditioners.h.

    {
      return factorize(mat);
    }

template<typename _Scalar >

template<typename MatType >

LeastSquareDiagonalPreconditioner& Eigen::LeastSquareDiagonalPreconditioner< _Scalar >::factorize

(

const MatType &

mat

)

[inline]

Reimplemented from Eigen::DiagonalPreconditioner< _Scalar >.

Definition at line 151 of file BasicPreconditioners.h.

    {
      // Compute the inverse squared-norm of each column of mat
      m_invdiag.resize(mat.cols());
      for(Index j=0; j<mat.outerSize(); ++j)
      {
        RealScalar sum = mat.innerVector(j).squaredNorm();
        if(sum>0)
          m_invdiag(j) = RealScalar(1)/sum;
        else
          m_invdiag(j) = RealScalar(1);
      }
      Base::m_isInitialized = true;
      return *this;
    }

template<typename _Scalar >

ComputationInfo Eigen::LeastSquareDiagonalPreconditioner< _Scalar >::info

(

)

[inline]

Reimplemented from Eigen::DiagonalPreconditioner< _Scalar >.

Definition at line 173 of file BasicPreconditioners.h.

{ return Success; }

---

The documentation for this class was generated from the following file:

• BasicPreconditioners.h