|
MOAB
4.9.3pre
|
|
MOAB
4.9.3pre
|
Base class for permutations. More...
#include <PermutationMatrix.h>

Public Types | |
| enum | { Flags = Traits::Flags, RowsAtCompileTime = Traits::RowsAtCompileTime, ColsAtCompileTime = Traits::ColsAtCompileTime, MaxRowsAtCompileTime = Traits::MaxRowsAtCompileTime, MaxColsAtCompileTime = Traits::MaxColsAtCompileTime } |
| typedef Traits::IndicesType | IndicesType |
| typedef Traits::StorageIndex | StorageIndex |
| typedef Matrix< StorageIndex, RowsAtCompileTime, ColsAtCompileTime, 0, MaxRowsAtCompileTime, MaxColsAtCompileTime > | DenseMatrixType |
| typedef PermutationMatrix < IndicesType::SizeAtCompileTime, IndicesType::MaxSizeAtCompileTime, StorageIndex > | PlainPermutationType |
| typedef PlainPermutationType | PlainObject |
| typedef Inverse< Derived > | InverseReturnType |
| typedef void | Scalar |
Public Member Functions | |
| template<typename OtherDerived > | |
| Derived & | operator= (const PermutationBase< OtherDerived > &other) |
| template<typename OtherDerived > | |
| Derived & | operator= (const TranspositionsBase< OtherDerived > &tr) |
| Derived & | operator= (const PermutationBase &other) |
| Index | rows () const |
| Index | cols () const |
| Index | size () const |
| template<typename DenseDerived > | |
| void | evalTo (MatrixBase< DenseDerived > &other) const |
| DenseMatrixType | toDenseMatrix () const |
| const IndicesType & | indices () const |
| IndicesType & | indices () |
| void | resize (Index newSize) |
| void | setIdentity () |
| void | setIdentity (Index newSize) |
| Derived & | applyTranspositionOnTheLeft (Index i, Index j) |
| Derived & | applyTranspositionOnTheRight (Index i, Index j) |
| InverseReturnType | inverse () const |
| InverseReturnType | transpose () const |
| template<typename Other > | |
| PlainPermutationType | operator* (const PermutationBase< Other > &other) const |
| template<typename Other > | |
| PlainPermutationType | operator* (const InverseImpl< Other, PermutationStorage > &other) const |
| Index | determinant () const |
Protected Member Functions | |
| template<typename OtherDerived > | |
| void | assignTranspose (const PermutationBase< OtherDerived > &other) |
| template<typename Lhs , typename Rhs > | |
| void | assignProduct (const Lhs &lhs, const Rhs &rhs) |
Private Types | |
| typedef internal::traits< Derived > | Traits |
| typedef EigenBase< Derived > | Base |
Friends | |
| template<typename Other > | |
| PlainPermutationType | operator* (const InverseImpl< Other, PermutationStorage > &other, const PermutationBase &perm) |
Base class for permutations.
| Derived | the derived class |
This class is the base class for all expressions representing a permutation matrix, internally stored as a vector of integers. The convention followed here is that if 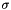 is a permutation, the corresponding permutation matrix
is a permutation, the corresponding permutation matrix 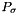 is such that if
is such that if  is the canonical basis, we have:
is the canonical basis, we have:
![\[ P_\sigma(e_i) = e_{\sigma(i)}. \]](form_27.png)
This convention ensures that for any two permutations 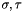 , we have:
, we have:
![\[ P_{\sigma\circ\tau} = P_\sigma P_\tau. \]](form_29.png)
Permutation matrices are square and invertible.
Notice that in addition to the member functions and operators listed here, there also are non-member operator* to multiply any kind of permutation object with any kind of matrix expression (MatrixBase) on either side.
Definition at line 46 of file PermutationMatrix.h.
typedef EigenBase<Derived> Eigen::PermutationBase< Derived >::Base [private] |
Reimplemented in Eigen::PermutationWrapper< _IndicesType >, Eigen::Map< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, _StorageIndex >, _PacketAccess >, Eigen::PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, _StorageIndex >, Eigen::PermutationMatrix< ColsAtCompileTime, MaxColsAtCompileTime >, Eigen::PermutationMatrix< Dynamic, Dynamic, StorageIndex >, and Eigen::PermutationMatrix< RowsAtCompileTime, MaxRowsAtCompileTime >.
Definition at line 49 of file PermutationMatrix.h.
| typedef Matrix<StorageIndex,RowsAtCompileTime,ColsAtCompileTime,0,MaxRowsAtCompileTime,MaxColsAtCompileTime> Eigen::PermutationBase< Derived >::DenseMatrixType |
Definition at line 63 of file PermutationMatrix.h.
| typedef Traits::IndicesType Eigen::PermutationBase< Derived >::IndicesType |
Reimplemented in Eigen::PermutationWrapper< _IndicesType >, Eigen::Map< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, _StorageIndex >, _PacketAccess >, Eigen::PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, _StorageIndex >, Eigen::PermutationMatrix< ColsAtCompileTime, MaxColsAtCompileTime >, Eigen::PermutationMatrix< Dynamic, Dynamic, StorageIndex >, and Eigen::PermutationMatrix< RowsAtCompileTime, MaxRowsAtCompileTime >.
Definition at line 53 of file PermutationMatrix.h.
| typedef Inverse<Derived> Eigen::PermutationBase< Derived >::InverseReturnType |
Definition at line 68 of file PermutationMatrix.h.
| typedef PlainPermutationType Eigen::PermutationBase< Derived >::PlainObject |
Definition at line 66 of file PermutationMatrix.h.
| typedef PermutationMatrix<IndicesType::SizeAtCompileTime,IndicesType::MaxSizeAtCompileTime,StorageIndex> Eigen::PermutationBase< Derived >::PlainPermutationType |
Definition at line 65 of file PermutationMatrix.h.
| typedef void Eigen::PermutationBase< Derived >::Scalar |
Definition at line 69 of file PermutationMatrix.h.
| typedef Traits::StorageIndex Eigen::PermutationBase< Derived >::StorageIndex |
Reimplemented in Eigen::Map< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, _StorageIndex >, _PacketAccess >, Eigen::PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, _StorageIndex >, Eigen::PermutationMatrix< ColsAtCompileTime, MaxColsAtCompileTime >, Eigen::PermutationMatrix< Dynamic, Dynamic, StorageIndex >, and Eigen::PermutationMatrix< RowsAtCompileTime, MaxRowsAtCompileTime >.
Definition at line 61 of file PermutationMatrix.h.
typedef internal::traits<Derived> Eigen::PermutationBase< Derived >::Traits [private] |
Reimplemented in Eigen::PermutationWrapper< _IndicesType >, Eigen::Map< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, _StorageIndex >, _PacketAccess >, Eigen::PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, _StorageIndex >, Eigen::PermutationMatrix< ColsAtCompileTime, MaxColsAtCompileTime >, Eigen::PermutationMatrix< Dynamic, Dynamic, StorageIndex >, and Eigen::PermutationMatrix< RowsAtCompileTime, MaxRowsAtCompileTime >.
Definition at line 48 of file PermutationMatrix.h.
| anonymous enum |
Definition at line 54 of file PermutationMatrix.h.
{
Flags = Traits::Flags,
RowsAtCompileTime = Traits::RowsAtCompileTime,
ColsAtCompileTime = Traits::ColsAtCompileTime,
MaxRowsAtCompileTime = Traits::MaxRowsAtCompileTime,
MaxColsAtCompileTime = Traits::MaxColsAtCompileTime
};
| Derived& Eigen::PermutationBase< Derived >::applyTranspositionOnTheLeft | ( | Index | i, |
| Index | j | ||
| ) | [inline] |
Multiplies *this by the transposition 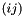 on the left.
on the left.
Definition at line 166 of file PermutationMatrix.h.
{
eigen_assert(i>=0 && j>=0 && i<size() && j<size());
for(Index k = 0; k < size(); ++k)
{
if(indices().coeff(k) == i) indices().coeffRef(k) = StorageIndex(j);
else if(indices().coeff(k) == j) indices().coeffRef(k) = StorageIndex(i);
}
return derived();
}
| Derived& Eigen::PermutationBase< Derived >::applyTranspositionOnTheRight | ( | Index | i, |
| Index | j | ||
| ) | [inline] |
Multiplies *this by the transposition 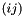 on the right.
on the right.
This is a fast operation, it only consists in swapping two indices.
Definition at line 185 of file PermutationMatrix.h.
| void Eigen::PermutationBase< Derived >::assignProduct | ( | const Lhs & | lhs, |
| const Rhs & | rhs | ||
| ) | [inline, protected] |
Definition at line 216 of file PermutationMatrix.h.
{
eigen_assert(lhs.cols() == rhs.rows());
for (Index i=0; i<rows();++i) indices().coeffRef(i) = lhs.indices().coeff(rhs.indices().coeff(i));
}
| void Eigen::PermutationBase< Derived >::assignTranspose | ( | const PermutationBase< OtherDerived > & | other | ) | [inline, protected] |
Definition at line 211 of file PermutationMatrix.h.
| Index Eigen::PermutationBase< Derived >::cols | ( | void | ) | const [inline] |
Reimplemented from Eigen::EigenBase< Derived >.
Definition at line 105 of file PermutationMatrix.h.
| Index Eigen::PermutationBase< Derived >::determinant | ( | ) | const [inline] |
This function is O(n) procedure allocating a buffer of n booleans.
Definition at line 253 of file PermutationMatrix.h.
{
Index res = 1;
Index n = size();
Matrix<bool,RowsAtCompileTime,1,0,MaxRowsAtCompileTime> mask(n);
mask.fill(false);
Index r = 0;
while(r < n)
{
// search for the next seed
while(r<n && mask[r]) r++;
if(r>=n)
break;
// we got one, let's follow it until we are back to the seed
Index k0 = r++;
mask.coeffRef(k0) = true;
for(Index k=indices().coeff(k0); k!=k0; k=indices().coeff(k))
{
mask.coeffRef(k) = true;
res = -res;
}
}
return res;
}
| void Eigen::PermutationBase< Derived >::evalTo | ( | MatrixBase< DenseDerived > & | other | ) | const [inline] |
Definition at line 112 of file PermutationMatrix.h.
{
other.setZero();
for (Index i=0; i<rows(); ++i)
other.coeffRef(indices().coeff(i),i) = typename DenseDerived::Scalar(1);
}
| const IndicesType& Eigen::PermutationBase< Derived >::indices | ( | ) | const [inline] |
const version of indices().
Reimplemented in Eigen::PermutationWrapper< _IndicesType >, Eigen::Map< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, _StorageIndex >, _PacketAccess >, Eigen::PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, _StorageIndex >, Eigen::PermutationMatrix< ColsAtCompileTime, MaxColsAtCompileTime >, Eigen::PermutationMatrix< Dynamic, Dynamic, StorageIndex >, and Eigen::PermutationMatrix< RowsAtCompileTime, MaxRowsAtCompileTime >.
Definition at line 130 of file PermutationMatrix.h.
{ return derived().indices(); }
| IndicesType& Eigen::PermutationBase< Derived >::indices | ( | ) | [inline] |
Reimplemented in Eigen::Map< PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, _StorageIndex >, _PacketAccess >, Eigen::PermutationMatrix< SizeAtCompileTime, MaxSizeAtCompileTime, _StorageIndex >, Eigen::PermutationMatrix< ColsAtCompileTime, MaxColsAtCompileTime >, Eigen::PermutationMatrix< Dynamic, Dynamic, StorageIndex >, and Eigen::PermutationMatrix< RowsAtCompileTime, MaxRowsAtCompileTime >.
Definition at line 132 of file PermutationMatrix.h.
{ return derived().indices(); }
| InverseReturnType Eigen::PermutationBase< Derived >::inverse | ( | ) | const [inline] |
Definition at line 196 of file PermutationMatrix.h.
{ return InverseReturnType(derived()); }
| PlainPermutationType Eigen::PermutationBase< Derived >::operator* | ( | const PermutationBase< Other > & | other | ) | const [inline] |
Definition at line 230 of file PermutationMatrix.h.
{ return PlainPermutationType(internal::PermPermProduct, derived(), other.derived()); }
| PlainPermutationType Eigen::PermutationBase< Derived >::operator* | ( | const InverseImpl< Other, PermutationStorage > & | other | ) | const [inline] |
Definition at line 238 of file PermutationMatrix.h.
{ return PlainPermutationType(internal::PermPermProduct, *this, other.eval()); }
| Derived& Eigen::PermutationBase< Derived >::operator= | ( | const PermutationBase< OtherDerived > & | other | ) | [inline] |
Copies the other permutation into *this
Definition at line 74 of file PermutationMatrix.h.
| Derived& Eigen::PermutationBase< Derived >::operator= | ( | const TranspositionsBase< OtherDerived > & | tr | ) | [inline] |
Assignment from the Transpositions tr
Definition at line 82 of file PermutationMatrix.h.
{
setIdentity(tr.size());
for(Index k=size()-1; k>=0; --k)
applyTranspositionOnTheRight(k,tr.coeff(k));
return derived();
}
| Derived& Eigen::PermutationBase< Derived >::operator= | ( | const PermutationBase< Derived > & | other | ) | [inline] |
This is a special case of the templated operator=. Its purpose is to prevent a default operator= from hiding the templated operator=.
Definition at line 94 of file PermutationMatrix.h.
| void Eigen::PermutationBase< Derived >::resize | ( | Index | newSize | ) | [inline] |
Resizes to given size.
Definition at line 136 of file PermutationMatrix.h.
{
indices().resize(newSize);
}
| Index Eigen::PermutationBase< Derived >::rows | ( | void | ) | const [inline] |
Reimplemented from Eigen::EigenBase< Derived >.
Definition at line 102 of file PermutationMatrix.h.
| void Eigen::PermutationBase< Derived >::setIdentity | ( | ) | [inline] |
Sets *this to be the identity permutation matrix
Definition at line 142 of file PermutationMatrix.h.
{
StorageIndex n = StorageIndex(size());
for(StorageIndex i = 0; i < n; ++i)
indices().coeffRef(i) = i;
}
| void Eigen::PermutationBase< Derived >::setIdentity | ( | Index | newSize | ) | [inline] |
Sets *this to be the identity permutation matrix of given size.
Definition at line 151 of file PermutationMatrix.h.
{
resize(newSize);
setIdentity();
}
| Index Eigen::PermutationBase< Derived >::size | ( | ) | const [inline] |
Reimplemented from Eigen::EigenBase< Derived >.
Definition at line 108 of file PermutationMatrix.h.
| DenseMatrixType Eigen::PermutationBase< Derived >::toDenseMatrix | ( | ) | const [inline] |
| InverseReturnType Eigen::PermutationBase< Derived >::transpose | ( | ) | const [inline] |
Definition at line 202 of file PermutationMatrix.h.
{ return InverseReturnType(derived()); }
| PlainPermutationType operator* | ( | const InverseImpl< Other, PermutationStorage > & | other, |
| const PermutationBase< Derived > & | perm | ||
| ) | [friend] |
Definition at line 246 of file PermutationMatrix.h.
{ return PlainPermutationType(internal::PermPermProduct, other.eval(), perm); }