|
MOAB: Mesh Oriented datABase
(version 5.4.1)
|
|
MOAB: Mesh Oriented datABase
(version 5.4.1)
|
3.MOAB API Design Philosophy and Summary
4.5. File Reader/Writer Interfaces
4.6. File Readers/Writers Packaged With MOAB
5.Parallel Mesh Representation and Query
5.1. Nomenclature & Representation
5.2. Parallel Mesh Initialization
5.3. Parallel Mesh Query Functions
5.4. Parallel Mesh Communication
6.Building MOAB-Based Applications
7.iMesh (ITAPS Mesh Interface) Implementation in MOAB
9.Structured Mesh Representation
11.Performance and Using MOAB Efficiently from Applications
13.Conclusions and Future Plans
In scientific computing, systems of partial differential equations (PDEs) are solved on computers. One of the most widely used methods to solve PDEs numerically is to solve over discrete neighborhoods or “elements” of the domain. Popular discretization methods include Finite Difference (FD), Finite Element (FE), and Finite Volume (FV). These methods require the decomposition of the domain into a discretized representation, which is referred to as a “mesh”. The mesh is one of the fundamental types of data linking the various tools in the analysis process (mesh generation, analysis, visualization, etc.). Thus, the representation of mesh data and operations on those data play a very important role in PDE-based simulations.
MOAB is a component for representing and evaluating mesh data. It is part of the Scalable Interfaces for Geometry and Mesh based Applications (SIGMA) toolkit [1]. MOAB can store structured and unstructured mesh, consisting of elements in the finite element “zoo”, along with polygons and polyhedra. The functional interface to MOAB is simple, consisting of only four fundamental data types. This data is quite powerful, allowing the representation of most types of metadata commonly found on the mesh. Internally, MOAB uses array-based storage for fine-grained data, which in many cases provides more efficient access, especially for large portions of mesh and associated data. MOAB is optimized for efficiency in space and time, based on access to mesh in chunks rather than through individual entities, while also versatile enough to support individual entity access. MOAB is also unique in that it maintains a completely parallel view of the mesh database so that queries to traverse the cells and manipulation of the grid in memory is scalable in parallel.
The MOAB data model consists of the following four fundamental types: mesh interface instance, mesh entities (vertex, edge, tri, etc.), sets, and tags. Entities are addressed through handles rather than pointers, to allow the underlying representation of an entity to change without changing the handle to that entity. Sets are arbitrary groupings of mesh entities and other sets. Sets also support parent/child relationships as a relation distinct from sets containing other sets. The directed graph provided by set parent/child relationships is useful for embedding graphs whose nodes include collections of mesh entities; this approach has been used to represent a wide variety of application-specific data, including geometric model topology, processor partitions, and various types of search trees. Tags are named data which can be assigned to the mesh as a whole, individual entities, or sets. Tags are a mechanism for attaching data to individual entities, and sets are a mechanism for describing relations between entities; the combination of these two mechanisms is a powerful yet simple interface for representing metadata or application-specific data.
Various mesh-related tools are provided with MOAB or can be used directly with MOAB. These tools can be used for mesh format translation (mbconvert), mesh skinning (Skinner class), solution transfer between meshes (MBCoupler tool), ray tracing and other geometric searches (OrientedBoxTreeTool, AdaptiveKDTree), visualization (vtkMOABReader tool), mesh optimization/smoothing (Mesquite interfaces), and relation between mesh and geometric models (the separately-packed Lasso tool). These tools are described later in this document.
MOAB is written in the C++ programming language, with applications interacting with MOAB mostly through its moab::Interface class. All of the MOAB functions and classes are isolated in and accessed through the moab namespace1. The remainder of this report gives class and function names without the “moab::” namespace qualification; unless otherwise noted, the namespace qualifier should be added to all class and function names referenced here. MOAB also implements the iMesh interface, which is specified in C but can be called directly from other languages. Almost all of the functionality in MOAB can be accessed through the iMesh interface. MOAB is developed and supported on the Linux and MacOS operating systems, as well as various HPC operating systems. MOAB can be used on parallel computing systems as well, including both clusters and high-end parallel systems like IBM BG/P and Cray systems. MOAB is released under a standard LGPL open source software license.
MOAB is used in several ways in various applications. MOAB serves as the underlying mesh data representation in several scientific computing applications [2], [3], [4], [5], [6]. MOAB can also be used as a mesh format translator, using readers and writers included in MOAB. MOAB has also been used as a bridge to couple results in multi-physics analysis and to link these applications with other mesh services [7] in order to consistently solve problems at scale.
The remainder of this guide is organized as follows. Section 2, “Getting Started”, provides a few simple examples of using MOAB to perform simple tasks on a mesh. Section 3 discusses the MOAB data model in more detail, including some aspects of the implementation. Section 4 summarizes the MOAB function API. Section 5 describes some of the tools included with MOAB, and the implementation of mesh readers/writers for MOAB. Section 6 describes how to build MOAB-based applications. Section 7 contains a brief description of MOAB’s relation to the iMesh mesh interface. Sections 8 and 9 discuss MOAB's representations of structured and spectral element meshes, respectively. Section 10 gives helpful hints for accessing MOAB in an efficient manner from applications. Section 11 gives a conclusion and future plans for MOAB development. Section 12 gives references cited in this report.
Several other sources of information about MOAB may also be of interest to readers. Meta-data conventions define how sets and /or tags are used together to represent various commonly-used simulation constructs in MOAB [8]. MOAB also has an active mailing list [9] to provide guidance and encourage discussions about usage and development of algorithms using MOAB. A separate mailing list [10] for MOAB-related release announcements and future guidance may also be subscribed by users. Potential users are encouraged to interact with the MOAB team using these mailing lists, and watch the SIGMA website [1] for updates.
1 Non-namespaced names are also provided for backward compatibility, with the “MB” prefix added to the class or variable name.
The MOAB data model describes the basic types used in MOAB and the language used to communicate that data to applications. This chapter describes that data model, along with some of the reasons for some of the design choices in MOAB.
MOAB is written in C++. The primary interface with applications is through member functions of the abstract base class Interface. The MOAB library is created by instantiating Core, which implements the Interface API. Multiple instances of MOAB can exist concurrently in the same application; mesh entities are not shared between these instances2. MOAB is most easily viewed as a database of mesh objects accessed through the instance. No other assumptions explicitly made about the nature of the mesh stored there; for example, there is no fundamental requirement that elements fill space or do not overlap each other geometrically.
2 One exception to this statement is when the parallel interface to MOAB is used; in this case, entity sharing between instances is handled explicitly using message passing. This is described in more detail in Section 5 of this document.
MOAB represents the following topological mesh entities: vertex, edge, triangle, quadrilateral, polygon, tetrahedron, pyramid, prism, knife, hexahedron, polyhedron. MOAB uses the EntityType enumeration to refer to these entity types (see Table 1). This enumeration has several special characteristics, chosen intentionally: the types begin with vertex, entity types are grouped by topological dimension, with lower-dimensional entities appearing before higher dimensions; the enumeration includes an entity type for sets (described in the next section); and MBMAXTYPE is included at the end of this enumeration, and can be used to terminate loops over type. In addition to these defined values, the an increment operator (++) is defined such that variables of type EntityType can be used as iterators in loops. MOAB refers to entities using “handles”. Handles are implemented as long integer data types, with the four highest-order bits used to store the entity type (mesh vertex, edge, tri, etc.) and the remaining bits storing the entity id. This scheme is convenient for applications because:
This handle implementation is exposed to applications intentionally, because of optimizations that it enables, and is unlikely to change in future versions.
| MBVERTEX = 0 | MBPRISM |
| MBEDGE | MBKNIFE |
| MBTRI | MBHEX |
| MBQUAD | MBPOLYHEDRON |
| MBPOLYGON | MBENTITYSET |
| MBTET | MBMAXTYPE |
| MBPYRAMID |
MOAB defines a special class for storing lists of entity handles, named Range. This class stores handles as a series of (start_handle, end_handle) subrange tuples. If a list of handles has large contiguous ranges, it can be represented in almost constant size using Range. Since entities are typically created in groups, e.g. during mesh generation or file import, a high degree of contiguity in handle space is typical. Range provides an interface similar to C++ STL containers like std::vector, containing iterator data types and functions for initializing and iterating over entity handles stored in the range. Range also provides functions for efficient Boolean operations like subtraction and intersection. Most API functions in MOAB come in both range-based and vector-based variants. By definition, a list of entities stored in an Range is always sorted, and can contain a given entity handle only once. Range cannot store the handle 0 (zero).
Typical usage of an Range object would look like:
using namespace moab; int my_function(Range &from_range) { int num_in_range = from_range.size(); Range to_range; Range::iterator rit; for (rit = from_range.begin(); rit != from_range.end(); ++rit) { EntityHandle this_ent = *rit; to_range.insert(this_ent); } }
Here, the range is iterated similar to how std::vector is iterated.
The term adjacencies is used to refer to those entities topologically connected to a given entity, e.g. the faces bounded by a given edge or the vertices bounding a given region. The same term is used for both higher-dimensional (or bounded) and lower-dimensional (or bounding) adjacent entities. MOAB provides functions for querying adjacent entities by target dimension, using the same functions for higher- and lower-dimension adjacencies. By default, MOAB stores the minimum data necessary to recover adjacencies between entities. When a mesh is initially loaded into MOAB, only entity-vertex (i.e. “downward”) adjacencies are stored, in the form of entity connectivity. When “upward” adjacencies are requested for the first time, e.g. from vertices to regions, MOAB stores all vertex-entity adjacencies explicitly, for all entities in the mesh. Non-vertex entity to entity adjacencies are never stored, unless explicitly requested by the application.
In its most fundamental form, a mesh need only be represented by its vertices and the entities of maximal topological dimension. For example, a hexahedral mesh can be represented as the connectivity of the hex elements and the vertices forming the hexes. Edges and faces in a 3D mesh need not be explicitly represented. We refer to such entities as “AEntities”, where ‘A’ refers to “Auxiliary”, “Ancillary”, and a number of other words mostly beginning with ‘A’. Individual AEntities are created only when requested by applications, either using mesh modification functions or by requesting adjacencies with a special “create if missing” flag passed as “true”. This reduces the overall memory usage when representing large meshes. Note entities must be explicitly represented before they can be assigned tag values or added to entity sets (described in following Sections).
Entity sets are also known as "mesh sets", or when the context is clear, not to be confused with std::set, just "sets". Entity sets are used to store arbitrary collections of entities and other sets. Sets are used for a variety of things in mesh-based applications, from the set of entities discretizing a given geometric model entity to the entities partitioned to a specific processor in a parallel finite element application. MOAB entity sets can also store parent/child relations with other entity sets, with these relations distinct from contains relations. Parent/child relations are useful for building directed graphs with graph nodes representing collections of mesh entities; this construct can be used, for example, to represent an interface of mesh faces shared by two distinct collections of mesh regions. MOAB also defines one special set, the “root set” or the interface itself; all entities are part of this set by definition. Defining a root set allows the use of a single set of MOAB API functions to query entities in the overall mesh as well as its subsets.
MOAB entity sets can be one of two distinct types: list-type entity sets preserve the order in which entities are added to the set, and can store a given entity handle multiple times in the same set; set-type sets are always ordered by handle, regardless of the order of addition to the set, and can store a given entity handle only once. This characteristic is assigned when the set is created, and cannot be changed during the set’s lifetime.
MOAB provides the option to track or not track entities in a set. When entities (and sets) are deleted by other operations in MOAB, they will also be removed from containing sets for which tracking has been enabled. This behavior is assigned when the set is created, and cannot be changed during the set’s lifetime. The cost of turning tracking on for a given set is sizeof(EntityHandle) for each entity added to the set; MOAB stores containing sets in the same list which stores adjacencies to other entities.
Using an entity set looks like the following:
using namespace moab; // load a file using MOAB, putting the loaded mesh into a file set EntityHandle file_set; ErrorCode rval = moab->create_meshset(MESHSET_SET, file_set); rval = moab->load_file(“fname.vtk”, &file_set); Range set_ents; // get all the 3D entities in the set rval = moab->get_entities_by_dimension(file_set, 3, set_ents);
Entity sets are often used in conjunction with tags (described in the next section), and provide a powerful mechanism to store a variety of meta-data with meshes.
Applications of a mesh database often need to attach data to mesh entities. The types of attached data are often not known at compile time, and can vary across individual entities and entity types. MOAB refers to this attached data as a “tag”. Tags can be thought of loosely as a variable, which can be given a distinct value for individual entities, entity sets, or for the interface itself. A tag is referenced using a handle, similarly to how entities are referenced in MOAB. Each MOAB tag has the following characteristics, which can be queried through the MOAB interface:
The storage type determines how tag values are stored on entities.
MOAB also supports variable-length tags, which can have a different length for each entity they are assigned to. Variable length tags are stored similarly to sparse tags.
The data type of a tag can either be one understood at compile time (integer, double, entity handle), in which case the tag value can be saved and restored properly to/from files and between computers of different architecture (MOAB provides a native HDF5-based save/restore format for this purpose; see Section 4.6). The opaque data type is used for character strings, or for allocating “raw memory” for use by applications (e.g. for storage application-defined structures or other abstract data types). These tags are saved and restored as raw memory, with no special handling for endian or precision differences.
An application would use the following code to attach a double-precision tag to vertices in a mesh, e.g. to assign a temperature field to those vertices:
using namespace moab; // load a file using MOAB and get the vertices ErrorCode rval = moab->load_file(“fname.vtk”); Range verts; rval = moab->get_entities_by_dimension(0, 0, verts); // create a tag called “TEMPERATURE” Tag temperature; double def_val = -1.0d-300, new_val = 273.0; rval = moab->tag_create(“TEMPERATURE”, sizeof(double), MB_TAG_DENSE, MB_TYPE_DOUBLE, temperature, &def_val); // assign a value to vertices for (Range::iterator vit = verts.begin(); vit != verts.end(); ++vit) rval = moab->tag_set_data(temperature, &(*rit), 1, &new_val);
The semantic meaning of a tag is determined by applications using it. However, to promote interoperability between applications, there are a number of tag names reserved by MOAB which are intended to be used by convention. Mesh readers and writers in MOAB use these tag conventions, and applications can use them as well to access the same data. Ref. [1] maintains an up-to-date list of conventions for meta-data usage in MOAB.
This section describes the design philosophy behind MOAB, and summarizes the functions, data types and enumerated variables in the MOAB API. A complete description of the MOAB API is available in online documentation in the MOAB distribution [11].
MOAB is designed to operate efficiently on collections of entities. Entities are often created or referenced in groups (e.g. the mesh faces discretizing a given geometric face, the 3D elements read from a file), with those groups having some form of temporal or spatial locality. The interface provides special mechanisms for reading data directly into the native storage used in MOAB, and for writing large collections of entities directly from that storage, to avoid data copies. MOAB applications structured to take advantage of that locality will typically operate more efficiently.
MOAB has been designed to maximize the flexibility of mesh data which can be represented. There is no explicit constraint on the geometric structure of meshes represented in MOAB, or on the connectivity between elements. In particular, MOAB allows the representation of multiple entities with the same exact connectivity; however, in these cases, explicit adjacencies must be used to distinguish adjacencies with AEntities bounding such entities.
The number of vertices used to represent a given topological entity can vary, depending on analysis needs; this is often the case in FEA. For example, applications often use “quadratic” or 10-vertex tetrahedral, with vertices at edge midpoints as well as corners. MOAB does not distinguish these variants by entity type, referring to all variants as “tetrahedra”. The number of vertices for a given entity is used to distinguish the variants, with canonical numbering conventions used to determine placement of the vertices [12]. This is similar to how such variations are represented in the Exodus [13] and Patran [14] file formats. In practice, we find that this simplifies coding in applications, since in many cases the handling of entities depends only on the number of corner vertices in the element. Some MOAB API functions provide a flag which determines whether corner or all vertices are requested.
The MOAB API is designed to balance complexity and ease of use. This balance is evident in the following general design characteristics:
Since these objectives are at odds with each other, tradeoffs had to be made between them. Some specific issues that came up are:
Table 2 lists basic data types and enumerated variables defined and used by MOAB. Values of the ErrorCode enumeration are returned from most MOAB functions, and can be compared to those listed in Appendix [ref-appendix].
MOAB uses several pre-defined tag names to define data commonly found in various mesh-based analyses. Ref. [8] and the {metadata.html}{meta-data conventions guide} provide an up-to-date decription as new conventions emerge for using sets and tags in MOAB applications.
| Enum / Type | Description |
|---|---|
| ErrorCode | Specific error codes returned from MOAB |
| EntityHandle | Type used to represent entity handles |
| Tag | Type used to represent tag handles |
| TagType | Type used to represent tag storage type |
| DataType | Type used to represent tag data type |
Table 3 lists the various groups of functions that comprise the MOAB API. This is listed here strictly as a reference to the various types of functionality supported by MOAB; for a more detailed description of the scope and syntax of the MOAB API, see the online documentation [11].
| Function group | Examples | Description |
|---|---|---|
| Constructor, destructor, interface | Interface, ~Core, query_interface | Construct/destroy interface; get pointer to read/write interface |
| Entity query | get_entities_by_dimension, get_entities_by_handle | Get entities by dimension, type, etc. |
| Adjacencies | get_adjacencies, set_adjacencies, add_adjacencies | Get topologically adjacent entities; set or add explicit adjacencies |
| Vertex coordinates | get_coords, set_coords | Get/set vertex coordinates |
| Connectivity | get_connectivity, set_connectivity | Get/set connectivity of non-vertex entities |
| Sets | create_meshset, add_entities, add_parent_child | Create and work with entity sets |
| Tags | tag_get_data, tag_create | Create, read, write tag data |
| Handles | type_from_handle, id_from_handle | Go between handles and types/ids |
| File handling | load_mesh, save_mesh | Read/write mesh files |
| Geometric dimension | get_dimension, set_dimension | Get/set geometric dimension of mesh |
| Mesh modification | create_vertex, delete_entity | Create or delete mesh entities |
| Information | list_entities, get_last_error | Get or print certain information |
| High-order nodes | high_order_node | Get information on high-order nodes |
| Canonical numbering | side_number | Get canonical numbering information |
3In iMesh, the whole mesh is specified by a special entity set handle, referred to as the “root set”.
4Note that STL vectors of entity handles can be input in this manner by using &vector[0] and vector.size() for the 1d vector address and size, respectively.
A number of mesh-based services are often used in conjunction with a mesh library. For example, parallel applications often need to visualize the mesh and associated data. Other services, like spatial interpolation or finding the faces on the “skin” of a 3D mesh, can be implemented more efficiently using knowledge of specific data structures in MOAB. Several of these services provided with MOAB are described in this chapter.
Visualization is one of the most common needs associated with meshes. The primary tool used to visualize MOAB meshes is VisIt [15]. Users can download a VisIt version that has the MOAB plugin pre-compiled (versions >= 2.12), and then select the MOAB format to directly visualize native files (default extension h5m) in HDF5 format. The visualization plugin has also been written with scalability in mind and can be launched on several processors to perform visualization and analysis of large datasets resulting from applications.
There are capabilities in VisIt for viewing and manipulation of tag data and some types of entity sets. Dense tag data is visualized using the same mechanisms used to view other field data in VisIt, e.g. using a pseudocolor plot; Material sets, neumann and dirichlet sets, along with parallel partition sets can be visualized using the subset capability.
To support parallel simulation, applications often need to partition a mesh into parts, designed to balance the load and minimize communication between sets. MOAB includes the mbpart tool for this purpose, constructed on the well-known Zoltan partitioning library [16] and Metis [17]. After computing the partition using Zoltan or Metis, MOAB stores the partition as either tags on individual entities in the partition, or as tagged sets, one set per part. Since a partition often exhibits locality similar to how the entities were created, storing it as sets (based on Range’s) is often more memory-efficient than an entity tag-based representation. Figure below shows a couple of partitioned meshes computed with mbpart with -z option for Zoltan and visualized in VisIt.

An operation commonly applied to mesh is to compute the outermost “skin” bounding a contiguous block of elements. This skin consists of elements of one fewer topological dimension, arranged in one or more topological balls on the boundary of the elements. The Skinner tool computes the skin of a mesh in a memory-efficient manner. Skinner uses knowledge about whether vertex-entity adjacencies and AEntities exist to minimize memory requirements and searching time required during the skinning process. This skin can be provided as a single collection of entities, or as sets of entities distinguished by forward and reverse orientation with respect to higher-dimensional entities in the set being skinned.
The following code fragment shows how Skinner can be used to compute the skin of a range of hex elements:
using namespace moab; Range hexes, faces; ErrorCode rval = moab->get_entities_by_dimension(0, 3, hexes); Skinner myskinner(moab); bool verts_too = false; ErrorCode rval = myskinner.find_skin(hexes, verts_too, faces);
Skinner can also skin a mesh based on geometric topology groupings imported with the mesh. The geometric topology groupings contain information about the mesh “owned” by each of the entities in the geometric model, e.g. the model vertices, edges, etc. Links between the mesh sets corresponding to those entities can be inferred directly from the mesh. Skinning a mesh this way will typically be much faster than doing so on the actual mesh elements, because there is no need to create and destroy interior faces on the mesh.
MOAB provides several mechanisms for spatial decomposition and searching in a mesh:
These trees have various space and time searching efficiencies. All are implemented based on entity sets and parent/child relations between those sets, allowing storage of a tree decomposition using MOAB’s native file storage mechanism (see Section 4.6.1). MOAB’s entity set implementation is specialized for memory efficiency when representing binary trees. Tree decompositions in MOAB have been used to implement fast ray tracing to support radiation transport [6], [18], solution coupling between meshes [2], [3], [7], and embedded boundary mesh generation [19]. MOAB also includes the DagMC tool to support several Monte Carlo radiation transport solvers by exposing queries related to ray tracing on the underlying geometry.
The following code fragment shows very basic use of AdaptiveKDTree. A range of entities is put in the tree; the leaf containing a given point is found, and the entities in that leaf are returned.
using namespace moab; // create the adaptive kd tree from a range of tets std::ostringstream options; options << "MAX_PER_LEAF=1;SPLITS_PER_DIR=1;PLANE_SET=0;"; FileOptions opts(options.str().c_str()); EntityHandle root; ErrorCode rval; AdaptiveKDTree tool( &moab ); rval = tool.build_tree( tets, &root, &opts); // get the overall bounding box corners const double * boxmax, * boxmin; boxmax = myTree.box_max(); boxmin = myTree.box_min; // get the tree leaf containing point xyz, and the tets in that leaf AdaptiveKDTreeIter treeiter; rval = myTree.point_search(xyz, treeiter); Range leaf_tets; rval = moab->get_entities_by_dimension(treeiter.handle(), 3, leaf_tets, false);
More detailed examples of using the various tree decompositions in MOAB can be found in [ref-treeexamples].
Mesh readers and writers communicate mesh into/out of MOAB from/to disk files. Reading a mesh often involves importing large sets of data, for example coordinates of all the nodes in the mesh. Normally, this process would involve reading data from the file into a temporary data buffer, then copying data from there into its destination in MOAB. To avoid the expense of copying data, MOAB has implemented a reader/writer interface that provides direct access to blocks of memory used to represent mesh.
The reader interface, declared in ReadUtilIface, is used to request blocks of memory for storing coordinate positions and element connectivity. The pointers returned from these functions point to the actual memory used to represent those data in MOAB. Once data is written to that memory, no further copying is done. This not only saves time, but it also eliminates the need to allocate a large memory buffer for intermediate storage of these data.
MOAB allocates memory for nodes and elements (and their corresponding dense tags) in chunks, to avoid frequent allocation/de-allocation of small chunks of memory. The chunk size used depends on from where the mesh is being created, and can strongly affect the performance (and memory layout) of MOAB. Since dense tags are allocated at the chunk size, this can also affect overall memory usage in cases where the mesh size is small but the number of dense tags or dense tag size is large. When creating vertices and elements through the normal MOAB API, default chunk sizes defined in the SequenceManager class are used. However, most of the file readers in MOAB allocate the exact amount of space necessary to represent the mesh being read. There are also a few exceptions to this:
Applications calling the reader interface functions directly can specify the allocation chunk size as an optional parameter.
The reader interface consists of the following functions:
The following code fragment illustrates the use of ReadUtilIface to read a mesh directly into MOAB’s native representation. This code assumes that connectivity is specified in terms of vertex indices, with vertex indices starting from 1.
// get the read iface from moab ReadUtilIface *iface; ErrorCode rval = moab->query_interface(iface); // allocate a block of vertex handles and read xyz’s into them std::vector<double*> arrays; EntityHandle startv, *starth; rval = iface->get_node_coords(3, num_nodes, 0, startv, arrays); for (int i = 0; i < num_nodes; i++) infile >> arrays[0][i] >> arrays[1][i] >> arrays[2][i]; // allocate block of hex handles and read connectivity into them rval = iface->get_element_connect(num_hexes, 8, MBHEX, 0, starth); for (int i = 0; i < 8*num_hexes; i++) infile >> starth[i]; // change connectivity indices to vertex handles for (int i = 0; i < 8*num_hexes; i++) starth[i] += startv-1;
The writer interface, declared in WriteUtilIface, provides functions that support writing vertex coordinates and element connectivity to storage locations input by the application. Assembling these data is a common task for writing mesh, and can be non-trivial when exporting only subsets of a mesh. The writer interface declares the following functions:
The following code fragment shows how to use WriteUtilIface to write the vertex coordinates and connectivity indices for a subset of entities.
using namespace moab; // get the write iface from moab WriteUtilIface *iface; ErrorCode rval = moab->query_interface(iface); // get all hexes the model, and choose the first 10 of those Range tmp_hexes, hexes, verts; rval = moab->get_entities_by_type(0, MBHEX, tmp_hexes); for (int i = 0; i < 10; i++) hexes.insert(tmp_hexes[i]); rval = iface->gather_nodes_from_elements(hexes, 0, verts); // assign vertex ids iface->assign_ids(verts, 0, 1); // allocate space for coordinates & write them std::vector<double*> arrays(3); for (int i = 0; i < 3; i++) arrays[i] = new double[verts.size()]; iface->get_node_coords(3, verts.size(), verts, 0, 1, arrays); // put connect’y in array, in the form of indices into vertex array std::vector<int> conn(8*hexes.size()); iface->get_element_connect(hexes.size(), 8, 0, hexes, 0, 1, &conn[0]);
MOAB has been designed to efficiently represent data and metadata commonly found in finite element mesh files. Readers and writers are included with MOAB which import/export specific types of metadata in terms of MOAB sets and tags, as described earlier in this document. The number of readers and writers in MOAB will probably grow over time, and so they are not enumerated here. See the src/io/README file in the MOAB source distribution for a current list of supported formats.
Because of its generic support for readers and writers, described in the previous section, MOAB is also a good environment for constructing new mesh readers and writers. The ReadTemplate and WriteTemplate classes in src/io are useful starting points for constructing new file readers/writers; applications are encouraged to submit their own readers/writers for inclusion in MOAB’s contrib/io directory in the MOAB source.
The usefulness of a file reader/writer is determined not only by its ability to read and write nodes and elements, but also in its ability to store the various types of meta-data included with the typical mesh. MOAB readers and writers are distinguished by their ability to preserve meta-data in meshes that they read and write. For example, MOAB’s CUB reader imports not only the mesh saved from CUBIT, but also the grouping of mesh entities into sets which reflect the geometric topology of the model used to generate the mesh. A more detailed description of meta-data conventions used in MOAB’s file readers and writers, and the individual file reader/writer header files in src/io for details about the specific readers and writers are available {metadata.html}{here}.
Three specific file readers in MOAB bear further discussion: MOAB’s native HDF5-based file reader/writer; the CUB reader, used to import mesh and meta-data represented in CUBIT; and the CGM reader, which imports geometric models. These are described next.
A mesh database must be able to save and restore the data stored in its data model, at least to the extent to which it understands the semantics of that data. MOAB defines an HDF5-based file format that can store data embedded in MOAB. By convention, these files are given an “.h5m” file extension. When reading or writing large amounts of data, it is recommended to use this file format, as it is the most complete and also the most efficient of the file readers/writers in MOAB.
CUBIT is a toolkit for generating tetrahedral and hexahedral finite element meshes from solid model geometry [20]. This tool saves and restores data in a custom “.cub” file, which stores both mesh and geometry (and data relating the two). The CUB reader in MOAB can import and interpret much of the meta-data information saved in .cub files. The information read from .cub files, and stored in the MOAB data model, includes:
Note that although information about model entities is recovered, MOAB by default does not depend on a solid modeling engine; this information is stored in the form of entity sets and parent/child relations between them.
The Common Geometry Module (CGM) [21] is a library for representing solid model and other types of solid geometry data. The CUBIT mesh generation toolkit uses CGM for its geometric modeling support, and CGM can restore geometric models in the exact state in which they were represented in CUBIT. MOAB contains a CGM reader, which can be enabled with a configure option. Using this reader, MOAB can read geometric models, and represent their model topology using entity sets linked by parent/child relations. The mesh in these models comes directly from the modeling engine faceting routines; these are the same facets used to visualize solid models in other graphics engines. When used in conjunction with the VisIt visualization tool (see Section 4.1), this provides a solution for visualizing geometric models. The figure below shows a model imported using MOAB’s CGM reader and visualized with VisIt.

Currently, the upward (vertex to entities) adjacencies are created and stored the first time a query requiring the adjacency is performed. Any non-vertex entity to entity adjacencies are performed using boolean operations on vertex-entity adjacencies. Because of this approach, such adjacency queries might become expensive with increasing dimension. We have added an alternative approach for obtaining adjacencies using the Array-based Half-Facet (AHF) representation[22]. The AHF uses sibling half-facets as a core abstraction which are generalizations of the opposite half-edge and half-face data structure for 2D and 3D manifold meshes. The AHF data structure consists of two essential maps: 1) the mapping between all sibling half-facets (sibhfs) and, 2) the mapping from each vertex to some incident half-facet (v2hf). The entire range of adjacencies (higher-, same- and lower-dimension) are computed using these two maps.
The easiest way to avail this feature is to configure MOAB with " --enable-ahf " option. The adjacency queries can then be performed through calls to the preserved interface function "get_adjacencies" returning the values in a standard vector. Currently, returning adjacent entityhandles in MOAB::Range is not supported for AHF-based queries. There is one key difference between the native MOAB (adjacency-list based) and AHF based adjacency calls using the "get_adjacencies" interface. In native MOAB adjacency calls, the same-dimensional queries return the query entities whereas for AHF it would return the same-dimensional entities connected to the query entities via a lower dimensional facet. Thus the entire range ( higher-dimensional, same-dimensional, lower-dimensional) of adjacencies can be obtained using the same interface. Similar to MOAB's native adjacency lists, the AHF maps are created during the first adjacency call which will make the first adjacency call expensive.
In the current release, AHF based adjacencies calls do not support the following cases:
The support for these would be gradually added in the next releases. In these cases, any adjacency call would revert back to MOAB's native adjacency list based queries.
If for some reason, the user does not want to configure MOAB with AHF but would still like to use the AHF-based adjacencies for certain queries, they could use the following three interface functions provided in the HalfFacetRep class which implements the AHF maps and adjacency queries:
TODO:: Other features to be added
Many applications require a hierarchy of successively refined meshes for a number of purposes such as convergence studies, to use multilevel methods like multigrid, generate large meshes in parallel computing to support increasing mesh sizes with increase in number of processors, etc. Uniform mesh refinement provides a simple and efficient way to generate such hierarchies via successive refinement of the mesh at a previous level. It also provides a natural hierarchy via parent and child type of relationship between entities of meshes at different levels. Generally, the standard nested refinement patterns used are the subdivision schemes from 1 to 4 for 2D (triangles, quads) and 1 to 8 for 3D (tets, hexes) entity types. However, many applications might require degree 3 or more for p-refinements.
MOAB supports generation of a mesh hierarchy i.e., a sequence of meshes with user specified degrees for each level of refinement, from an initial unstructured mesh with support for higher degrees of refinement (supported degrees are listed later). Thus MOAB supports multi-degree and multi-level mesh generation via uniform refinement. The following figure shows the initial and most refined mesh for four simple meshes to illustrate the multi-degree capability.

Applications using mesh hierarchies require two types of mesh access: intralevel and interlevel. The intralevel access involves working with the mesh at a particular level whereas interlevel access involves querying across different levels. In order to achieve data locality with reduced cache misses for efficient intralevel mesh access, old vertices in the previous i.e. immediate parent mesh are duplicated in the current level. All the entities thus created for the current level use the new entityhandles of old vertices along with the handles of the new vertices. This design makes mesh at each level of the hierarchy independent of those at previous levels. For each mesh in the hierarchy, a MESHSET is created and all entities of the mesh are added to this MESHSET. Thus the meshes of the hierarchy are accessible via these level-wise MESHSET handles.
For interlevel queries, separate interface functions are defined to allow queries across different levels. These queries mainly allow obtaining the parent at some specified parent level for a child from later levels and vice versa. The child-parent queries are not restricted to a level difference of one as the internal array-based layout of the memory allows traversing between different levels via index relations.
The hierarchy generation capability is implemented in NestedRefine class. In Table 4, the user interface functions are briefly described. The main hierarchy generating function takes as input a sequence of refinement degrees to be used for generating mesh at each level from the previous level, the total number of levels in the hierarchy. It returns EntityHandles for the meshsets created for the mesh at each level. The number of levels in the hierarchy is prefixed (by the user) and cannot change during hierarchy generation. An example of how to generate a hierarchy can be found under examples/UniformRefinement.cpp.
The next three functions for getting the coordinates, connectivity and adjacencies are standard operations to access and query a mesh. The coordinates and connectivity functions, which are similar to their counterparts in MOAB Interface class, allows one to query the mesh at a specific level via its level index. The reason to provide such similar functions is to increase computational efficiency by utilizing the direct access to memory pointers to EntitySequences created during hierarchy generation under the NestedRefine class instead of calling the standard interfaces where a series of calls have to made before the EntitySequence of the requested entity is located. It is important to note that any calls to the standard interfaces available under Interface class should work.
The underlying mesh data structure used for uniform refinement is the AHF datastructure implemented in HalfFacetRep class. This direct dependence on HalfFacetRep class removes the necessity to configure MOAB with --enable-ahf flag in order to use the uniform refinement capability. During the creation of an object of the NestedRefine class, it will internally initialize all the relevant AHF maps for the mesh in memory. During mesh hierarchy generation, after the creation of mesh at each level all the relevant AHF maps are updated to allow query over it.
For interlevel queries, currently three kinds of queries are supported. The child to parent function allows querying for a parent in any of the previous levels (including the initial mesh). The parent to child, on the other hand, returns all its children from a requested child level. These two types of queries are only supported for entities, not vertices. A separate vertex to entities function is provided which returns entities from the previous level that are either incident or contain this vertex.
| Function group | Function | Description |
|---|---|---|
| Hierarchy generation | generate_mesh_hierarchy | Generate a mesh hierarchy with a given sequence of refinement degree for each level. |
| Vertex coordinates | get_coordinates | Get vertex coordinates |
| Connectivity | get_connectivity | Get connectivity of non-vertex entities |
| Adjacencies | get_adjacencies | Get topologically adjacent entities |
| Interlevel Queries | child_to_parent | Get the parent entity of a child from a specified parent level |
| Interlevel Queries | parent_to_child | Get all children of the parent from a specified child level |
| Interlevel Queries | vertex_to_entities | Get all the entities in the previous level incident on or containing the vertex |
| Mesh Dimension | EntityTypes | Degree | Number of children |
|---|---|---|---|
| 1 | MBEDGE | 2, 3, 5 | 2, 3, 5 |
| 2 | MBTRI, MBQUAD | 2, 3, 5 | 4, 9, 25 |
| 3 | MBTET, MBHEX | 2, 3 | 8, 27 |
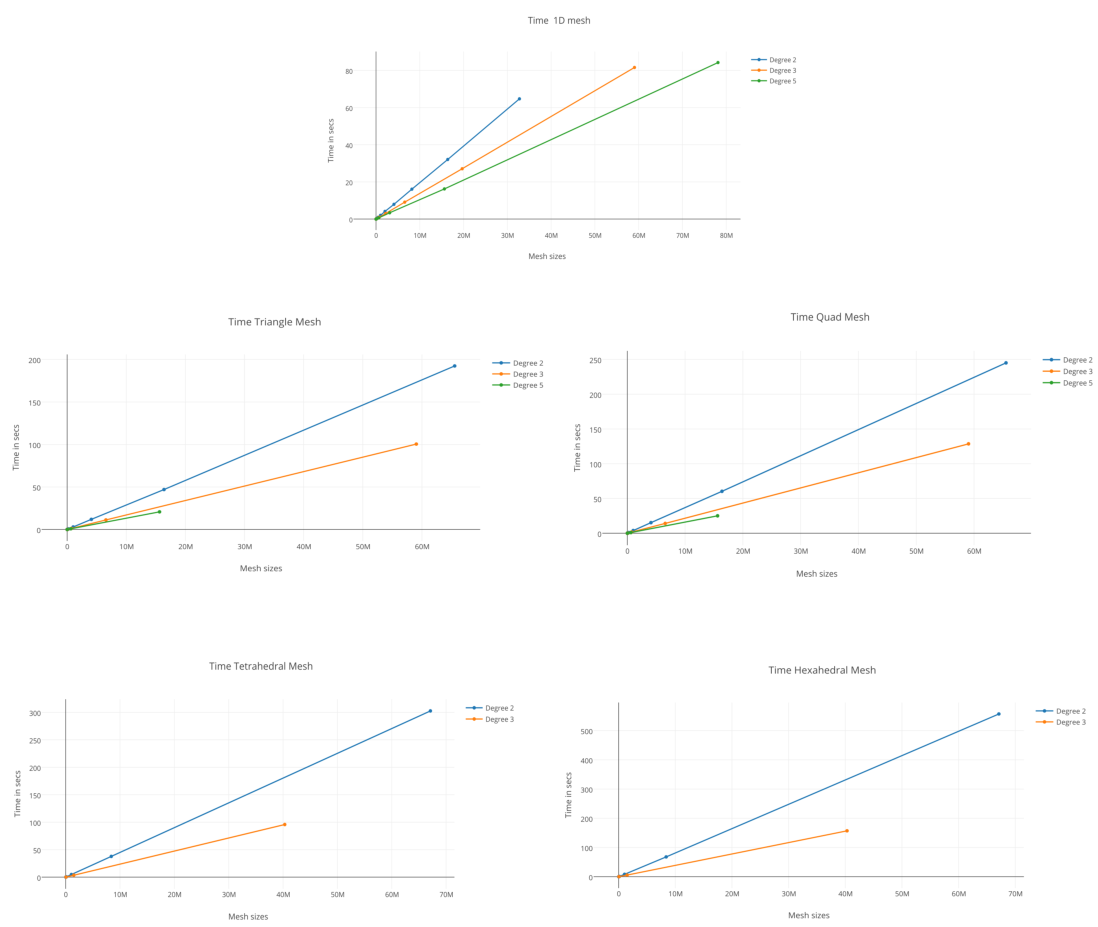
In Table 5, the currently supported degrees of refinement for each dimension is listed along with the number of children created for each such degree for a single entity. The following figure shows the cpu times(serial run) for generating hierarchies with various degrees of refinement for each dimension and can be used by the user to guide in choosing the degrees of refinement for the hierarchy. For example, if a multilevel hierarchy is required, a degree 2 refinement per level would give a gradually increasing mesh with more number of levels. If a very refined mesh is desired quickly, then a small hierarchy with high-order refinement should be generated.
Current support:
TODO:
A parallel mesh representation must strike a careful balance between providing an interface to mesh similar to that of a serial mesh, while also allowing the discovery of parallel aspects of the mesh and performance of parallel mesh-based operations efficiently. MOAB supports a spatial domain-decomposed view of a parallel mesh, where each subdomain is assigned to a processor, lower-dimensional entities on interfaces between subdomains are shared between processors, and ghost entities can be exchanged with neighboring processors. Locally, each subdomain, along with any locally-represented ghost entities, are accessed through a local MOAB instance. Parallel aspects of the mesh, e.g. whether entities are shared, on an interface, or ghost entities, are embedded in the same data model (entities, sets, tags, interface) used in the rest of MOAB. MOAB provides a suite of parallel functions for initializing and communicating with a parallel mesh, along with functions to query the parallel aspects of the mesh.
Before discussing how to access parallel aspects of a mesh, several terms need to be defined:
Shared entity: An entity shared by one or several other processors.
Multi-shared entity: An entity shared by more than two processors.
Owning Processor: Each shared entity is owned by exactly one processor. This processor has the right to set tag values on the entity and have those values propagated to any sharing processors.
Part: The collection of entities assigned to a given processor. When reading mesh in parallel, the entities in a Part, along with any lower-dimensional entities adjacent to those, will be read onto the assigned processor.
Partition: A collection of Parts which take part in parallel collective communication, usually associated with an MPI communicator.
Interface: A collection of mesh entities bounding entities in multiple parts. Interface entities are owned by a single processor, but are represented on all parts/processors they bound.
Ghost entity: A shared, non-interface, non-owned entity.
Parallel status: A characteristic of entities and sets represented in parallel. The parallel status, or “pstatus”, is represented by a bit field stored in an unsigned character, with bit values as described in Table 6.
| Bit | Name | Represents |
|---|---|---|
| 0x1 | PSTATUS_NOT_OWNED | Not owned by the local processor |
| 0x2 | PSTATUS_SHARED | Shared by exactly two processorstd> |
| 0x4 | PSTATUS_MULTISHARED | Shared by three or more processors |
| 0x8 | PSTATUS_INTERFACE | Part of lower-dimensional interface shared by multiple processors |
| 0x10 | PSTATUS_GHOST | Non-owned, non-interface entities represented locally |
Parallel functionality is described in the following sections and in [26]. First, methods to load a mesh into a parallel representation are described; next, functions for accessing parallel aspects of a mesh are described; functions for communicating mesh and tag data are described.
Parallel mesh is initialized in MOAB in several steps:
These steps can be executed by a single call to MOAB’s load_file function, using the procedure described in Section 5.2.1. Or, they can be executed in smaller increments calling specific functions in MOAB’s ParallelComm class, as described in Section 5.2.2. Closely related to the latter method is the handling of communicators, described in more detail in Section.
In the file reading approach, a mesh must contain some definition of the partition (the assignment of mesh, usually regions, to processors). Partitions can be derived from other set structures already on the mesh, or can be computed explicitly for that purpose by tools like mbzoltan (see Section 4.2). For example, geometric volumes used to generate the mesh, and region-based material type assignments, are both acceptable partitions. In addition to defining the groupings of regions into parts, the assignment of specific parts to processors can be done implicitly or using additional data stored with the partition.
MOAB implements several specific methods for loading mesh into a parallel representation:
The READ_DELETE and BCAST_DELETE methods are supported for all file types MOAB is able to read, while READ_PART is only implemented for MOAB’s native HDF5-based file format and netcdf and pnetcdf files from climate application.
Various other options control the selection of part sets or other details of the parallel read process. For example, the application can specify the tags, and optionally tag values, which identify parts, and whether those parts should be distributed according to tag value or using round-robin assignment.
The options used to specify loading method, the data used to identify parts, and other parameters controlling the parallel read process, are shown in Table 7.
| Option | Value | Description | |||
|---|---|---|---|---|---|
| PARTITION | <tag_name> | Sets with the specified tag name should be used as part sets | |||
| PARTITION_VAL | <val1, val2-val3, ...> | Integer values to be combined with tag name, with ranges input using val1, val2-val3. Not meaningful unless PARTITION option is also given. | |||
| PARTITION_DISTRIBUTE | (none) | If present, or values are not input using PARTITION_VAL, sets with tag indicated in PARTITION option are partitioned across processors in round-robin fashion. | |||
| PARALLEL_RESOLVE_SHARED_ENTS | <pd.sd> | Resolve entities shared between processors, where partition is made up of pd- dimensional entities, and entities of dimension sd and lower should be resolved. | |||
| PARALLEL_GHOSTS | <gd.bd.nl[.ad]> | Exchange ghost elements at shared inter-processor interfaces. Ghost elements of dimension gd will be exchanged. Ghost elements are chosen going through bd-dimensional interface entities. Number of layers of ghost elements is specified in nl. If ad is present, lower-dimensional entities bounding exchanged ghost entities will also be exchanged; allowed values for ad are 1 (exchange bounding edges), 2 (faces), or 3 (edges and faces). | PARALLEL_COMM | <id> | Use the ParallelComm with index <id>. Index for a ParallelComm object can be checked with ParallelComm::get_id(), and a ParallelComm with a given index can be retrieved using ParallelComm::get_pcomm(id). |
CPUTIME
(none)
Print cpu time required for each step of parallel read & initialization.
MPI_IO_RANK
<r>
If read method requires reading mesh onto a single processor, processor with rank r is used to do that read.
Several example option strings controlling parallel reading and initialization are:
“PARALLEL=READ_DELETE; PARTITION=MATERIAL_SET; PARTITION_VAL=100, 200, 600-700”: The whole mesh is read by every processor; this processor keeps mesh in sets assigned the tag whose name is “MATERIAL_SET” and whose value is any one of 100, 200, and 600-700 inclusive.
“PARALLEL=READ_PART; PARTITION=PARALLEL_PARTITION, PARTITION_VAL=2”: Each processor reads only its mesh; this processor, whose rank is 2, is responsible for elements in a set with the PARALLEL_PARTITION tag whose value is 2. This would by typical input for a mesh which had already been partitioned with e.g. Zoltan or Parmetis.
“PARALLEL=BCAST_DELETE; PARTITION=GEOM_DIMENSION, PARTITION_VAL=3, PARTITION_DISTRIBUTE”: The root processor reads the file and broadcasts the whole mesh to all processors. If a list is constructed with entity sets whose GEOM_DIMENSION tag is 3, i.e. sets corresponding to geometric volumes in the original geometric model, this processor is responsible for all elements with index R+iP, i >= 0 (i.e. a round-robin distribution).
After creating the local mesh on each processor, an application can call the following functions in ParallelComm to establish information on shared mesh entities. See the [http://ftp.mcs.anl.gov/pub/fathom/moab-docs/HelloParMOAB_8cpp-example.html example] in the MOAB source tree for a complete example of how this is done from an application.
The ParallelComm constructor takes arguments for an MPI communicator and a MOAB instance. The ParallelComm instance stores the MPI communicator, and registers itself with the MOAB instance. Applications can specify the ParallelComm index to be used for a given file operation, thereby specifying the MPI communicator for that parallel operation. For example:
using namespace moab; // pass a communicator to the constructor, getting back the index MPI_Comm my_mpicomm; int pcomm_index; ParallelComm my_pcomm(moab, my_mpicomm, &pcomm_index); // write the pcomm index into a string option char load_opt[32]; sprintf(load_opt, "PARALLEL=BCAST_DELETE;PARALLEL_COMM=%d", pcomm_index); // specify that option in a parallel read operation ErrorCode rval = moab->load_file(load_opt, fname, ...)
In the above code fragment, the ParallelComm instance with index pcomm_index will be used in the parallel file read, so that the operation executes over the specified MPI communicator. If no ParallelComm instance is specified for a parallel file operation, a default instance will be defined, using MPI_COMM_WORLD.
Applications needing to retrieve a ParallelComm instance created previously and stored with the MOAB instance, e.g. by a different code component, can do so using a static function on ParallelComm:
ParallelComm *my_pcomm = ParallelComm::get_pcomm(moab, pcomm_index);
ParallelComm also provides the ParallelComm::get_all_pcomm function, for retrieving all ParallelComm instances stored with a MOAB instance. For syntax and usage of this function, see the MOAB online documentation for ParallelComm.hpp [11].
Various functions are commonly used in parallel mesh-based applications. Functions marked as being collective must be called collectively for all processors that are members of the communicator associated with the ParallelComm instance used for the call.
ParallelComm::get_pstatus: Get the parallel status for the entity.
ParallelComm::get_pstatus_entities: Get all entities whose pstatus satisfies (pstatus & val).
ParallelComm::get_owner: Get the rank of the owning processor for the specified entity.
ParallelComm::get_owner_handle: Get the rank of the owning processor for the specified entity, and the entity's handle on the owning processor.
ParallelComm::get_sharing_data: Get the sharing processor(s) and handle(s) for an entity or entities. Various overloaded versions are available, some with an optional “operation” argument, where Interface::INTERSECT or Interface::UNION can be specified. This is similar to the operation arguments to Interface::get_adjacencies.
ParallelComm::get_shared_entities: Get entities shared with the given processor, or with all processors. This function has optional arguments for specifying dimension, whether interface entities are requested, and whether to return just owned entities.
ParallelComm::get_interface_procs: Return all processors with whom this processor shares an interface.
ParallelComm::get_comm_procs: Return all processors with whom this processor communicates.
Once a parallel mesh has been initialized, applications can call the ParallelComm::exchange_tags function for exchanging tag values between processors. This function causes the owning processor to send the specified tag values for all shared, owned entities to other processors sharing those entities. Asynchronous communication is used to hide latency, and only point-to-point communication is used in these calls.
There are two primary mechanisms supported by MOAB for building applications, one based on MOAB-defined make variables, and the other based on the use of libtool and autoconf. Both assume the use of a “make”-based build system.
The easiest way to incorporate MOAB into an application’s build process is to include the “moab.make” file into the application’s Makefile, adding the make variables MOAB_INCLUDES and MOAB_LIBS_LINK to application’s compile and link commands, respectively. MOAB_INCLUDES contains compiler options specifying the location of MOAB include files, and any preprocessor definitions required by MOAB. MOAB_LIBS_LINK contains both the options telling where libraries can be found, and the link options which incorporate those libraries into the application. Any libraries depended on by the particular configuration of MOAB are included in that definition, e.g. the HDF5 library. Using this method to incorporate MOAB is the most straightforward; for example, the following Makefile is used to build one of the example problems packaged with the MOAB source:
include ${MOAB_LIB_DIR}/moab.make
GetEntities : GetEntities.o
${CXX} $< ${MOAB_LIBS_LINK} -o $@
.cpp.o :
${CXX} ${MOAB_INCLUDES} -c $<
Here, the MOAB_LIB_DIR environment variable or make argument definition specifies where the MOAB library is installed; this is also the location of the moab.make file. Once that file has been included, MOAB_INCLUDES and MOAB_LIBS_LINK can be used, as shown.
Other make variables are defined in the moab.make file which simplify building applications:
The second method for incorporating MOAB into an application’s build system is to use autoconf and libtool. MOAB is configured using these tools, and generates the “.la” files that hold information on library dependencies that can be used in application build systems also based on autoconf and libtool. Further information on this subject is beyond the scope of this User’s Guide; see the “.la” files as installed by MOAB, and contact the MOAB developer’s mailing list [9] for more details.
iMesh is a common API to mesh data developed as part of the Interoperable Tools for Advanced Petascale Simulations (ITAPS) project [23]. Applications using the iMesh interface can operate on any implementation of that interface, including MOAB. MOAB-based applications can take advantage of other services implemented on top of iMesh, including the MESQUITE mesh improvement toolkit [24].
MOAB’s native interface is accessed through the Interface abstract C++ base class. Wrappers are not provided in other languages; rather, applications wanting to access MOAB from those languages should do so through iMesh. In most cases, the data models and functionality available through MOAB and iMesh are identical. However, there are a few differences, subtle and not-so-subtle, between the two:
SPARSE tags used by default: MOAB’s iMesh implementation creates SPARSE tags by default, because of semantic requirements of other tag-related functions in iMesh. To create DENSE tags through iMesh, use the iMesh_createTagWithOptions extension function (see below).
Higher-order elements: ITAPS currently handles higher-order elements (e.g. a 10-node tetrahedron and a 27-node hexahedra) [23]. As described in [sec-entities], MOAB supports higher-order entities by allowing various numbers of vertices to define topological entities like quadrilateral or tetrahedron. Applications can specify flags to the connectivity and adjacency functions specifying whether corner or all vertices are requested.
Self-adjacencies: In MOAB’s native interface, entities are always self-adjacent6; that is, adjacencies of equal dimension requested from an entity will always include that entity, while from iMesh will not include that entity.
Option strings: The iMesh specification requires that options in the options string passed to various functions (e.g. iMesh_load) be prepended with the implementation name required to parse them, and delimited with spaces. Thus, a MOAB-targeted option would appear as “moab:PARALLEL=READ_PART moab:PARTITION=MATERIAL_SET”.
To provide complete MOAB support from other languages through iMesh, a collection of iMesh extension functions are also available. A general description of these extensions appears below; for a complete description, see the online documentation for iMesh-extensions.h [11].
As required by the iMesh specification, MOAB generates the “iMesh-Defs.inc” file and installs it with the iMesh and MOAB libraries. This file defines make variables which can be used to build iMesh-based applications. The method used here is quite similar to that used for MOAB itself (see Section 6). In particular, the IMESH_INCLUDES and IMESH_LIBS make variables can be used with application compile and link commands, respectively, with other make variables similar to those provided in moab.make also available.
Note that using the iMesh interface from Fortran-based applications requires a compiler that supports Cray pointers, along with the pass-by-value (VAL) extension. Almost all compilers support those extensions; however, if using the gcc series of compilers, you must use gfortran 4.3 or later.
5There are currently no implementations of this interface.
6iMesh and MOAB both define adjacencies using the topological concept of closure. Since the closure of an entity includes the entity itself, the d-dimensional entities on the closure of a given entity should include the entity itself.
A Python interface to MOAB's essential core functionality and a few other tools has been added as of Version 5.0. The pymoab module can be used to interactively interrogate existing mesh files or prototype MOAB-based algorithms. It can also be connected to other Python applications or modules for generation, manipulation, and visualization of a MOAB mesh and mesh data. Examples of this can be found in the laplaciansmoother.py and yt2moab.py files. Interaction with the PyMOAB interface is intended to be somewhat analagous to interaction with the MOAB C++ API. A simple example of file loading and mesh interrogation can be found in interrogate_mesh.py
PyMOAB uses NumPy internally to represent data and vertex coordinates though other properly formed data structures can be used to create vertices, set data, etc. Data and vertex coordinates will always be returned in the form of NumPy arrays, however.
EntityHandles are represented by Python long integers. Arrays of these values are commonly returned from calls as MOAB Ranges.
MOAB ErrorCodes - Errors are automatically checked internally by the PyMOAB instance, raising various exceptions depending on the error that occurs. These exceptions can be handled as raised from the functions or acceptable error values returned can also be specified via the exceptions parameter common to all PyMOAB functions in which case no exception will be raised.
Documentation for PyMOAB functions is provided as part of this User's Guide, but can also be accessed in the Python interpreter by calling `help(<function_or_method>)`.
Examples of PyMOAB usage can be found in the /examples/python/ directory.
A structured mesh is defined as a D-dimensional mesh whose interior vertices have 2D connected edges. Structured mesh can be stored without connectivity, if certain information is kept about the parametric space of each structured block of mesh. MOAB can represent structured mesh with implicit connectivity, saving approximately 57% of the storage cost compared to an unstructured representation7. Since connectivity must be computed on the fly, these queries execute a bit slower than those for unstructured mesh. More information on the theory, and design behind MOAB's structured mesh representation can be found in [8].
Currently, MOAB's structured mesh representation can only be used by creating structured mesh at runtime; that is, structured mesh is saved/restored in an unstructured format in MOAB's HDF5-based native save format. For more details on how to use MOAB's structured mesh representation, see the scdseq_test.cpp source file in the test/ directory.
7 This assumes vertex coordinates are represented explicitly, and that there are approximately the same number of vertices and hexahedra in a structured hex mesh.
The Spectral Element Method (SEM) is a high-order method, using a polynomial Legendre interpolation basis with Gauss-Lobatto quadrature points, in contrast to the Lagrange basis used in (linear) finite elements [25]. SEM obtains exponential convergence with decreasing mesh characteristic sizes, and codes implementing this method typically have high floating-point intensity, making the method highly efficient on modern CPUs. Most Nth-order SEM codes require tensor product cuboid (quad/hex) meshes, with each d-dimensional element containing (N+1)^d degrees of freedom (DOFs). There are various methods for representing SEM meshes and solution fields on them; this document discusses these methods and the tradeoffs between them. The mesh parts of this discussion are given in terms of the iMesh mesh interface and its implementation by the MOAB mesh library.
The figure above shows a two-dimensional 3rd-order SEM mesh consisting of four quadrilaterals. For this mesh, each quadrilateral has (N+1)^2=16 DOFs, with corner and edge degrees of freedom shared between neighboring quadrilaterals.
There are various representations of this mesh in a mesh database like MOAB, depending on how DOFs are related to mesh entities and tags on those entities. We mention several possible representations:
As a convenience for applications, functions could also be provided for important tasks, like assembling the vertex handles for an entity in lexographic order (useful for option 2 above), and getting an array of tag values in lexicographic order (for option 3 above).
There are various competing tradeoffs in the various representation types. These include:
The lower-memory option (storing variables on vertices and assembling into lexicographically-ordered arrays for application use) usually ends up costing more in memory anyway, since applications must allocate their own storage for these arrays. On the other hand, certain applications will always choose to do that, instead of sharing storage with MOAB for these variables. In the case where applications do share memory with MOAB, other tools would need to interpret the lexicographically-ordered field arrays specially, instead of simply treating the vertex tags as a point-based field.
In choosing the right MOAB representation for spectral meshes, we are trying to balance a) minimal memory usage, b) access to properly-ordered and -aligned tag storage, and c) maximal compatibility with tools likely to use MOAB. The solution we propose is to use a representation most like option 2) above, with a few optional behaviors based on application requirements.
In brief, we propose to represent elements using the linear, FE-ordered connectivity list (containing only corner vertices from the spectral element), with field variables written to either vertices, lexicographically-ordered arrays on elements, or both, and with a lexicographically-ordered array (stored on tag SPECTRAL_VERTICES) of all (corner+higher-order) vertices stored on elements. In the either/or case, the choice will be evident from the tag size and the entities on which the tag is set. In the both case, the tag name will have a “-LEX” suffix for the element tags, and the size of the element tag will be (N+1)^2 times that of the vertex-based tag. Finally, the file set containing the spectral elements (or the root set, if no file set was input to the read) will contain a “SPECTRAL_ORDER” tag whose value is N. These conventions are described in the “Metadata Information” document distributed with the MOAB source code.
MOAB is designed to operate efficiently on groups of entities and for large meshes. Applications will be most efficient when they operate on entities in groups, especially groups which are close in their order of creation. The MOAB API is structured to encourage operations on groups of entities. Conversely, MOAB will not perform as well as other libraries if there are frequent deletion and creation of entities. For those types of applications, a mesh library using a C++ object-based representation is more appropriate. In this section, performance of MOAB when executing a variety of tasks is described, and compared to that of other representations. Of course, these metrics are based on the particular models and environments where they are run, and may or may not be representative of other application types.
One useful measure of MOAB performance is in the representation and query of a large mesh. MOAB includes a performance test, located in the test/perf directory, in which a single rectangular region of hexahedral elements is created then queried; the following steps are performed:
This test can be run on your system to determine the runtime and memory performance for these queries in MOAB.
Errors are handled through the routine MBError(). This routine calls MBTraceBackErrorHandler(), the default error handler which tries to print a traceback.
The arguments to MBTraceBackErrorHandler() are the line number where the error occurred, the function where error was detected, the file in which the error was detected, the corresponding directory, the error message, and the error type.
A small set of macros is used to make the error handling lightweight. These macros are used throughout the MOAB libraries and can be employed by the application programmer as well. When an error is first detected, one should set it by calling
MB_SET_ERR(err_code, err_msg);
Note, err_msg can be a string literal, or a C++ style output stream with << operators, such that the error message string is formated, like
MB_SET_ERR(MB_FAILURE, "Failed " << n << " times");
The user should check the return codes for all MOAB routines (and possibly user-defined routines as well) with
ErrorCode rval = MOABRoutine(...);MB_CHK_ERR(rval);
To pass back a new error message (if rval is not MB_SUCCESS), use
ErrorCode rval = MOABRoutine(...);MB_CHK_SET_ERR(rval, "User specified error message string (or stream)");
If this procedure is followed throughout all of the user’s libraries and codes, any error will by default generate a clean traceback of the location of the error.
In addition to the basic macros mentioned above, there are some variations, such as (for more information, refer to src/moab/ErrorHandler.hpp):
The error control mechanism are enabled by default if a MOAB Core instance is created. Otherwise, the user needs to call MBErrorHandler_Init() and MBErrorHandler_Finalize() at the application level in the main function. For example code on error handling, please refer to examples/TestErrorHandling.cpp, examples/TestErrorHandlingPar.cpp and examples/ErrorHandlingSimulation.cpp.
MOAB, a Mesh-Oriented datABase, provides a simple but powerful data abstraction to structured and unstructured mesh, and makes that abstraction available through a function API. MOAB provides the mesh representation for the VERDE mesh verification tool, which demonstrates some of the powerful mesh metadata representation capabilities in MOAB. MOAB includes modules that import mesh in the ExodusII, CUBIT .cub and Vtk file formats, as well as the capability to write mesh to ExodusII, all without licensing restrictions normally found in ExodusII-based applications. MOAB also has the capability to represent and query structured mesh in a way that optimizes storage space using the parametric space of a structured mesh; see Ref. [17] for details.
Initial results have demonstrated that the data abstraction provided by MOAB is powerful enough to represent many different kinds of mesh data found in real applications, including geometric topology groupings and relations, boundary condition groupings, and inter-processor interface representation. Our future plans are to further explore how these abstractions can be used in the design through analysis process.
[1] Mahadevan, Vijay S., Iulian Grindeanu, Rajeev Jain, Patrick Shriwise, Navamita Ray, Paul Wilson, Tautges, Timothy J., "SIGMA -- MOAB.", URL: {http://sigma.mcs.anl.gov/}{http://sigma.mcs.anl.gov/}
[2] Mahadevan, Vijay S., Iulian Grindeanu, Robert Jacob, and Jason Sarich. "Improving climate model coupling through a complete mesh representation: a case study with E3SM (v1) and MOAB (v5. x).", Geosci. Model Dev. Discuss., https://doi.org/10.5194/gmd-2018-280, in review, 2018.
[3] Mahadevan, Vijay S., Elia Merzari, Timothy Tautges, Rajeev Jain, Aleksandr Obabko, Michael Smith, and Paul Fischer. "High-resolution coupled physics solvers for analysing fine-scale nuclear reactor design problems." Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 372, no. 2021 (2014): 20130381.
[4] Yan, Mi, Kirk Jordan, Dinesh Kaushik, Michael Perrone, Vipin Sachdeva, Timothy J. Tautges, and John Magerlein. "Coupling a basin modeling and a seismic code using MOAB." Procedia Computer Science 9 (2012): 986-993.
[5] Jacob, Robert, Jayesh Krishna, Xiabing Xu, Tim Tautges, Iulian Grindeanu, Rob Latham, Kara Peterson et al. "ParNCL and ParGAL: Data-parallel tools for postprocessing of large-scale Earth science data." Procedia Computer Science 18 (2013): 1245-1254.
[6] Bohm, Tim D., Mohamed E. Sawan, Steve T. Jackson, and Paul PH Wilson. "Detailed nuclear analysis of ITER ELM coils." Fusion Engineering and Design 87, no. 5-6 (2012): 657-661.
[7] Tautges, Timothy J., and Alvaro Caceres. "Scalable parallel solution coupling for multiphysics reactor simulation." In Journal of Physics: Conference Series, vol. 180, no. 1, p. 012017. IOP Publishing, 2009.
[8] Tautges, Timothy J. "MOAB-SD: integrated structured and unstructured mesh representation." Engineering With Computers 20, no. 3 (2004): 286-293.
[9] MOAB Users and Developers Email List., moab-dev@mcs.anl.gov.
[10] MOAB Announcement Email List., moab-announce@mcs.anl.gov.
[11] MOAB online documentation., http://ftp.mcs.anl.gov/pub/fathom/moab-docs/index.html
[12] T.J. Tautges, “Canonical numbering systems for finite-element codes,” Communications in Numerical Methods in Engineering, vol. Online, Mar. 2009.
[13] L.A. Schoof and V.R. Yarberry, EXODUS II: A Finite Element Data Model, Albuquerque, NM: Sandia National Laboratories, 1994.
[14] M. PATRAN, “PATRAN User’s Manual,” 2005.
[15] VisIt User's Guide.
[16] Devine, Karen, Erik Boman, Robert Heaphy, Bruce Hendrickson, and Courtenay Vaughan. "Zoltan data management service for parallel dynamic applications." Computing in Science & Engineering 4, no. 2 (2002): 90.
[17] METIS - Serial Graph Partitioning and Fill-reducing Matrix Ordering. http://glaros.dtc.umn.edu/gkhome/views/metis
[18] Tautges, Timothy J., Paul PH Wilson, Jason A. Kraftcheck, Brandon M. Smith, and Douglass L. Henderson. "Acceleration techniques for direct use of CAD-based geometries in Monte Carlo radiation transport." (2009).
[19] Kim, Hong-Jun, and Timothy J. Tautges. "EBMesh: An embedded boundary meshing tool." In Proceedings of the 19th International Meshing Roundtable, pp. 227-242. Springer, Berlin, Heidelberg, 2010.
[20] G.D. Sjaardema, T.J. Tautges, T.J. Wilson, S.J. Owen, T.D. Blacker, W.J. Bohnhoff, T.L. Edwards, J.R. Hipp, R.R. Lober, and S.A. Mitchell, CUBIT mesh generation environment Volume 1: Users manual, Sandia National Laboratories, May 1994, 1994.
[21] T.J. Tautges, “CGM: A geometry interface for mesh generation, analysis and other applications,” Engineering with Computers, vol. 17, 2001, pp. 299-314.
[22] V. Dyedov, N. Ray, D.Einstein, X. Jiao, T. Tautges, “AHF: Array-based half-facet data structure for mixed-dimensional and non-manifold meshes”, In Proceedings of 22nd International Meshing Roundtable, Orlando, Florida, October 2013.
[23] Li, Xiaolin. Interoperable Technologies for Advanced Petascale Simulations. No. 41293. Stony Brook University, 2013.
[24] Knupp, Patrick. "Mesh quality improvement for SciDAC applications." In Journal of Physics: Conference Series, vol. 46, no. 1, p. 458. IOP Publishing, 2006.
[25] Deville, Michel O., Paul F. Fischer, Paul F. Fischer, and E. H. Mund. High-order methods for incompressible fluid flow. Vol. 9. Cambridge university press, 2002.
[26] T. J. Tautges, J. A. Kraftcheck, N. Bertram, V. Sachdeva and J. Magerlein, "Mesh Interface Resolution and Ghost Exchange in a Parallel Mesh Representation," 2012 IEEE 26th International Parallel and Distributed Processing Symposium Workshops & PhD Forum, Shanghai, 2012, pp. 1670-1679, doi: 10.1109/IPDPSW.2012.208. Table of Contents