LU decomposition of a matrix with complete pivoting, and related features. More...

#include <FullPivLU.h>

Inheritance diagram for Eigen::FullPivLU< _MatrixType >:

Collaboration diagram for Eigen::FullPivLU< _MatrixType >:

Public Types
enum	{ MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }
typedef _MatrixType	MatrixType
typedef SolverBase< FullPivLU >	Base
typedef internal::plain_row_type < MatrixType, StorageIndex > ::type	IntRowVectorType
typedef internal::plain_col_type < MatrixType, StorageIndex > ::type	IntColVectorType
typedef PermutationMatrix < ColsAtCompileTime, MaxColsAtCompileTime >	PermutationQType
typedef PermutationMatrix < RowsAtCompileTime, MaxRowsAtCompileTime >	PermutationPType
typedef MatrixType::PlainObject	PlainObject
Public Member Functions
	FullPivLU ()
	Default Constructor.
	FullPivLU (Index rows, Index cols)
	Default Constructor with memory preallocation.
template<typename InputType >
	FullPivLU (const EigenBase< InputType > &matrix)
template<typename InputType >
FullPivLU &	compute (const EigenBase< InputType > &matrix)
const MatrixType &	matrixLU () const
Index	nonzeroPivots () const
RealScalar	maxPivot () const
const PermutationPType &	permutationP () const
const PermutationQType &	permutationQ () const
const internal::kernel_retval < FullPivLU >	kernel () const
const internal::image_retval < FullPivLU >	image (const MatrixType &originalMatrix) const
template<typename Rhs >
const Solve< FullPivLU, Rhs >	solve (const MatrixBase< Rhs > &b) const
internal::traits< MatrixType > ::Scalar	determinant () const
FullPivLU &	setThreshold (const RealScalar &threshold)
FullPivLU &	setThreshold (Default_t)
RealScalar	threshold () const
Index	rank () const
Index	dimensionOfKernel () const
bool	isInjective () const
bool	isSurjective () const
bool	isInvertible () const
const Inverse< FullPivLU >	inverse () const
MatrixType	reconstructedMatrix () const
Index	rows () const
Index	cols () const
template<typename RhsType , typename DstType >
EIGEN_DEVICE_FUNC void	_solve_impl (const RhsType &rhs, DstType &dst) const
template<bool Conjugate, typename RhsType , typename DstType >
EIGEN_DEVICE_FUNC void	_solve_impl_transposed (const RhsType &rhs, DstType &dst) const
Protected Member Functions
void	computeInPlace ()
Static Protected Member Functions
static void	check_template_parameters ()
Protected Attributes
MatrixType	m_lu
PermutationPType	m_p
PermutationQType	m_q
IntColVectorType	m_rowsTranspositions
IntRowVectorType	m_colsTranspositions
Index	m_det_pq
Index	m_nonzero_pivots
RealScalar	m_maxpivot
RealScalar	m_prescribedThreshold
bool	m_isInitialized
bool	m_usePrescribedThreshold

Detailed Description

template<typename _MatrixType>
class Eigen::FullPivLU< _MatrixType >

LU decomposition of a matrix with complete pivoting, and related features.

Template Parameters:

_MatrixType the type of the matrix of which we are computing the LU decomposition

This class represents a LU decomposition of any matrix, with complete pivoting: the matrix A is decomposed as 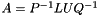$A = P^{-1} L U Q^{-1}$ where L is unit-lower-triangular, U is upper-triangular, and P and Q are permutation matrices. This is a rank-revealing LU decomposition. The eigenvalues (diagonal coefficients) of U are sorted in such a way that any zeros are at the end.

This decomposition provides the generic approach to solving systems of linear equations, computing the rank, invertibility, inverse, kernel, and determinant.

This LU decomposition is very stable and well tested with large matrices. However there are use cases where the SVD decomposition is inherently more stable and/or flexible. For example, when computing the kernel of a matrix, working with the SVD allows to select the smallest singular values of the matrix, something that the LU decomposition doesn't see.

The data of the LU decomposition can be directly accessed through the methods matrixLU(), permutationP(), permutationQ().

As an exemple, here is how the original matrix can be retrieved:

Output:

See also:: MatrixBase::fullPivLu(), MatrixBase::determinant(), MatrixBase::inverse()

Definition at line 57 of file FullPivLU.h.

Member Typedef Documentation

template<typename _MatrixType >

typedef SolverBase<FullPivLU> Eigen::FullPivLU< _MatrixType >::Base

Reimplemented from Eigen::SolverBase< FullPivLU< _MatrixType > >.

Definition at line 62 of file FullPivLU.h.

template<typename _MatrixType >

typedef internal::plain_col_type<MatrixType, StorageIndex>::type Eigen::FullPivLU< _MatrixType >::IntColVectorType

Definition at line 71 of file FullPivLU.h.

template<typename _MatrixType >

typedef internal::plain_row_type<MatrixType, StorageIndex>::type Eigen::FullPivLU< _MatrixType >::IntRowVectorType

Definition at line 70 of file FullPivLU.h.

template<typename _MatrixType >

typedef _MatrixType Eigen::FullPivLU< _MatrixType >::MatrixType

Definition at line 61 of file FullPivLU.h.

template<typename _MatrixType >

typedef PermutationMatrix<RowsAtCompileTime, MaxRowsAtCompileTime> Eigen::FullPivLU< _MatrixType >::PermutationPType

Definition at line 73 of file FullPivLU.h.

template<typename _MatrixType >

typedef PermutationMatrix<ColsAtCompileTime, MaxColsAtCompileTime> Eigen::FullPivLU< _MatrixType >::PermutationQType

Definition at line 72 of file FullPivLU.h.

template<typename _MatrixType >

typedef MatrixType::PlainObject Eigen::FullPivLU< _MatrixType >::PlainObject

Definition at line 74 of file FullPivLU.h.

Member Enumeration Documentation

template<typename _MatrixType >

anonymous enum

Enumerator:

MaxRowsAtCompileTime
MaxColsAtCompileTime

Definition at line 66 of file FullPivLU.h.

         {
      MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime,
      MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime
    };

Constructor & Destructor Documentation

template<typename MatrixType >

Eigen::FullPivLU< MatrixType >::FullPivLU ( )

Default Constructor.

The default constructor is useful in cases in which the user intends to perform decompositions via LU::compute(const MatrixType&).

Definition at line 418 of file FullPivLU.h.

  : m_isInitialized(false), m_usePrescribedThreshold(false)
{
}

template<typename MatrixType >

Eigen::FullPivLU< MatrixType >::FullPivLU	(	Index	rows,
		Index	cols
	)

Default Constructor with memory preallocation.

Like the default constructor but with preallocation of the internal data according to the specified problem size.

See also:: FullPivLU()

Definition at line 424 of file FullPivLU.h.

  : m_lu(rows, cols),
    m_p(rows),
    m_q(cols),
    m_rowsTranspositions(rows),
    m_colsTranspositions(cols),
    m_isInitialized(false),
    m_usePrescribedThreshold(false)
{
}

template<typename MatrixType >

template<typename InputType >

Eigen::FullPivLU< MatrixType >::FullPivLU ( const EigenBase< InputType > & matrix ) [explicit]

Constructor.

Parameters:

matrix the matrix of which to compute the LU decomposition. It is required to be nonzero.

Definition at line 437 of file FullPivLU.h.

  : m_lu(matrix.rows(), matrix.cols()),
    m_p(matrix.rows()),
    m_q(matrix.cols()),
    m_rowsTranspositions(matrix.rows()),
    m_colsTranspositions(matrix.cols()),
    m_isInitialized(false),
    m_usePrescribedThreshold(false)
{
  compute(matrix.derived());
}

Member Function Documentation

template<typename _MatrixType >

template<typename RhsType , typename DstType >

void Eigen::FullPivLU< _MatrixType >::_solve_impl	(	const RhsType &	rhs,
		DstType &	dst
	)		const

Definition at line 715 of file FullPivLU.h.

{
  /* The decomposition PAQ = LU can be rewritten as A = P^{-1} L U Q^{-1}.
  * So we proceed as follows:
  * Step 1: compute c = P * rhs.
  * Step 2: replace c by the solution x to Lx = c. Exists because L is invertible.
  * Step 3: replace c by the solution x to Ux = c. May or may not exist.
  * Step 4: result = Q * c;
  */

  const Index rows = this->rows(),
              cols = this->cols(),
              nonzero_pivots = this->rank();
  eigen_assert(rhs.rows() == rows);
  const Index smalldim = (std::min)(rows, cols);

  if(nonzero_pivots == 0)
  {
    dst.setZero();
    return;
  }

  typename RhsType::PlainObject c(rhs.rows(), rhs.cols());

  // Step 1
  c = permutationP() * rhs;

  // Step 2
  m_lu.topLeftCorner(smalldim,smalldim)
      .template triangularView<UnitLower>()
      .solveInPlace(c.topRows(smalldim));
  if(rows>cols)
    c.bottomRows(rows-cols) -= m_lu.bottomRows(rows-cols) * c.topRows(cols);

  // Step 3
  m_lu.topLeftCorner(nonzero_pivots, nonzero_pivots)
      .template triangularView<Upper>()
      .solveInPlace(c.topRows(nonzero_pivots));

  // Step 4
  for(Index i = 0; i < nonzero_pivots; ++i)
    dst.row(permutationQ().indices().coeff(i)) = c.row(i);
  for(Index i = nonzero_pivots; i < m_lu.cols(); ++i)
    dst.row(permutationQ().indices().coeff(i)).setZero();
}

template<typename _MatrixType >

template<bool Conjugate, typename RhsType , typename DstType >

void Eigen::FullPivLU< _MatrixType >::_solve_impl_transposed	(	const RhsType &	rhs,
		DstType &	dst
	)		const

Definition at line 763 of file FullPivLU.h.

{
  /* The decomposition PAQ = LU can be rewritten as A = P^{-1} L U Q^{-1},
   * and since permutations are real and unitary, we can write this
   * as   A^T = Q U^T L^T P,
   * So we proceed as follows:
   * Step 1: compute c = Q^T rhs.
   * Step 2: replace c by the solution x to U^T x = c. May or may not exist.
   * Step 3: replace c by the solution x to L^T x = c.
   * Step 4: result = P^T c.
   * If Conjugate is true, replace "^T" by "^*" above.
   */

  const Index rows = this->rows(), cols = this->cols(),
    nonzero_pivots = this->rank();
   eigen_assert(rhs.rows() == cols);
  const Index smalldim = (std::min)(rows, cols);

  if(nonzero_pivots == 0)
  {
    dst.setZero();
    return;
  }

  typename RhsType::PlainObject c(rhs.rows(), rhs.cols());

  // Step 1
  c = permutationQ().inverse() * rhs;

  if (Conjugate) {
    // Step 2
    m_lu.topLeftCorner(nonzero_pivots, nonzero_pivots)
        .template triangularView<Upper>()
        .adjoint()
        .solveInPlace(c.topRows(nonzero_pivots));
    // Step 3
    m_lu.topLeftCorner(smalldim, smalldim)
        .template triangularView<UnitLower>()
        .adjoint()
        .solveInPlace(c.topRows(smalldim));
  } else {
    // Step 2
    m_lu.topLeftCorner(nonzero_pivots, nonzero_pivots)
        .template triangularView<Upper>()
        .transpose()
        .solveInPlace(c.topRows(nonzero_pivots));
    // Step 3
    m_lu.topLeftCorner(smalldim, smalldim)
        .template triangularView<UnitLower>()
        .transpose()
        .solveInPlace(c.topRows(smalldim));
  }

  // Step 4
  PermutationPType invp = permutationP().inverse().eval();
  for(Index i = 0; i < smalldim; ++i)
    dst.row(invp.indices().coeff(i)) = c.row(i);
  for(Index i = smalldim; i < rows; ++i)
    dst.row(invp.indices().coeff(i)).setZero();
}

template<typename _MatrixType >

static void Eigen::FullPivLU< _MatrixType >::check_template_parameters ( ) [inline, static, protected]

Definition at line 400 of file FullPivLU.h.

    {
      EIGEN_STATIC_ASSERT_NON_INTEGER(Scalar);
    }

template<typename _MatrixType >

Index Eigen::FullPivLU< _MatrixType >::cols ( void ) const [inline]

Returns:: the number of columns.

See also:: rows(), ColsAtCompileTime

Reimplemented from Eigen::EigenBase< FullPivLU< _MatrixType > >.

Definition at line 386 of file FullPivLU.h.

{ return m_lu.cols(); }

template<typename MatrixType >

template<typename InputType >

FullPivLU< MatrixType > & Eigen::FullPivLU< MatrixType >::compute ( const EigenBase< InputType > & matrix )

Computes the LU decomposition of the given matrix.

Parameters:

matrix the matrix of which to compute the LU decomposition. It is required to be nonzero.

Returns:: a reference to *this

Definition at line 451 of file FullPivLU.h.

{
  check_template_parameters();

  // the permutations are stored as int indices, so just to be sure:
  eigen_assert(matrix.rows()<=NumTraits<int>::highest() && matrix.cols()<=NumTraits<int>::highest());

  m_isInitialized = true;
  m_lu = matrix.derived();

  computeInPlace();

  return *this;
}

template<typename MatrixType >

void Eigen::FullPivLU< MatrixType >::computeInPlace ( ) [protected]

Definition at line 467 of file FullPivLU.h.

{
  const Index size = m_lu.diagonalSize();
  const Index rows = m_lu.rows();
  const Index cols = m_lu.cols();

  // will store the transpositions, before we accumulate them at the end.
  // can't accumulate on-the-fly because that will be done in reverse order for the rows.
  m_rowsTranspositions.resize(m_lu.rows());
  m_colsTranspositions.resize(m_lu.cols());
  Index number_of_transpositions = 0; // number of NONTRIVIAL transpositions, i.e. m_rowsTranspositions[i]!=i

  m_nonzero_pivots = size; // the generic case is that in which all pivots are nonzero (invertible case)
  m_maxpivot = RealScalar(0);

  for(Index k = 0; k < size; ++k)
  {
    // First, we need to find the pivot.

    // biggest coefficient in the remaining bottom-right corner (starting at row k, col k)
    Index row_of_biggest_in_corner, col_of_biggest_in_corner;
    typedef internal::scalar_score_coeff_op<Scalar> Scoring;
    typedef typename Scoring::result_type Score;
    Score biggest_in_corner;
    biggest_in_corner = m_lu.bottomRightCorner(rows-k, cols-k)
                        .unaryExpr(Scoring())
                        .maxCoeff(&row_of_biggest_in_corner, &col_of_biggest_in_corner);
    row_of_biggest_in_corner += k; // correct the values! since they were computed in the corner,
    col_of_biggest_in_corner += k; // need to add k to them.

    if(biggest_in_corner==Score(0))
    {
      // before exiting, make sure to initialize the still uninitialized transpositions
      // in a sane state without destroying what we already have.
      m_nonzero_pivots = k;
      for(Index i = k; i < size; ++i)
      {
        m_rowsTranspositions.coeffRef(i) = i;
        m_colsTranspositions.coeffRef(i) = i;
      }
      break;
    }

    RealScalar abs_pivot = internal::abs_knowing_score<Scalar>()(m_lu(row_of_biggest_in_corner, col_of_biggest_in_corner), biggest_in_corner);
    if(abs_pivot > m_maxpivot) m_maxpivot = abs_pivot;

    // Now that we've found the pivot, we need to apply the row/col swaps to
    // bring it to the location (k,k).

    m_rowsTranspositions.coeffRef(k) = row_of_biggest_in_corner;
    m_colsTranspositions.coeffRef(k) = col_of_biggest_in_corner;
    if(k != row_of_biggest_in_corner) {
      m_lu.row(k).swap(m_lu.row(row_of_biggest_in_corner));
      ++number_of_transpositions;
    }
    if(k != col_of_biggest_in_corner) {
      m_lu.col(k).swap(m_lu.col(col_of_biggest_in_corner));
      ++number_of_transpositions;
    }

    // Now that the pivot is at the right location, we update the remaining
    // bottom-right corner by Gaussian elimination.

    if(k<rows-1)
      m_lu.col(k).tail(rows-k-1) /= m_lu.coeff(k,k);
    if(k<size-1)
      m_lu.block(k+1,k+1,rows-k-1,cols-k-1).noalias() -= m_lu.col(k).tail(rows-k-1) * m_lu.row(k).tail(cols-k-1);
  }

  // the main loop is over, we still have to accumulate the transpositions to find the
  // permutations P and Q

  m_p.setIdentity(rows);
  for(Index k = size-1; k >= 0; --k)
    m_p.applyTranspositionOnTheRight(k, m_rowsTranspositions.coeff(k));

  m_q.setIdentity(cols);
  for(Index k = 0; k < size; ++k)
    m_q.applyTranspositionOnTheRight(k, m_colsTranspositions.coeff(k));

  m_det_pq = (number_of_transpositions%2) ? -1 : 1;
}

template<typename MatrixType >

internal::traits< MatrixType >::Scalar Eigen::FullPivLU< MatrixType >::determinant ( ) const

Returns:: the determinant of the matrix of which *this is the LU decomposition. It has only linear complexity (that is, O(n) where n is the dimension of the square matrix) as the LU decomposition has already been computed.

Note:: This is only for square matrices.; For fixed-size matrices of size up to 4, MatrixBase::determinant() offers optimized paths.

Warning:: a determinant can be very big or small, so for matrices of large enough dimension, there is a risk of overflow/underflow.

See also:: MatrixBase::determinant()

Definition at line 551 of file FullPivLU.h.

{
  eigen_assert(m_isInitialized && "LU is not initialized.");
  eigen_assert(m_lu.rows() == m_lu.cols() && "You can't take the determinant of a non-square matrix!");
  return Scalar(m_det_pq) * Scalar(m_lu.diagonal().prod());
}

template<typename _MatrixType >

Index Eigen::FullPivLU< _MatrixType >::dimensionOfKernel ( ) const [inline]

Returns:: the dimension of the kernel of the matrix of which *this is the LU decomposition.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 325 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      return cols() - rank();
    }

template<typename _MatrixType >

const internal::image_retval<FullPivLU> Eigen::FullPivLU< _MatrixType >::image ( const MatrixType & originalMatrix ) const [inline]

Returns:: the image of the matrix, also called its column-space. The columns of the returned matrix will form a basis of the image (column-space).

Parameters:

originalMatrix the original matrix, of which *this is the LU decomposition. The reason why it is needed to pass it here, is that this allows a large optimization, as otherwise this method would need to reconstruct it from the LU decomposition.

Note:: If the image has dimension zero, then the returned matrix is a column-vector filled with zeros.; This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Example:

Output:

See also:: kernel()

Definition at line 200 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      return internal::image_retval<FullPivLU>(*this, originalMatrix);
    }

template<typename _MatrixType >

const Inverse<FullPivLU> Eigen::FullPivLU< _MatrixType >::inverse ( ) const [inline]

Returns:: the inverse of the matrix of which *this is the LU decomposition.

Note:: If this matrix is not invertible, the returned matrix has undefined coefficients. Use isInvertible() to first determine whether this matrix is invertible.

See also:: MatrixBase::inverse()

Definition at line 376 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      eigen_assert(m_lu.rows() == m_lu.cols() && "You can't take the inverse of a non-square matrix!");
      return Inverse<FullPivLU>(*this);
    }

template<typename _MatrixType >

bool Eigen::FullPivLU< _MatrixType >::isInjective ( ) const [inline]

Returns:: true if the matrix of which *this is the LU decomposition represents an injective linear map, i.e. has trivial kernel; false otherwise.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 338 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      return rank() == cols();
    }

template<typename _MatrixType >

bool Eigen::FullPivLU< _MatrixType >::isInvertible ( ) const [inline]

Returns:: true if the matrix of which *this is the LU decomposition is invertible.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 363 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      return isInjective() && (m_lu.rows() == m_lu.cols());
    }

template<typename _MatrixType >

bool Eigen::FullPivLU< _MatrixType >::isSurjective ( ) const [inline]

Returns:: true if the matrix of which *this is the LU decomposition represents a surjective linear map; false otherwise.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 351 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      return rank() == rows();
    }

template<typename _MatrixType >

const internal::kernel_retval<FullPivLU> Eigen::FullPivLU< _MatrixType >::kernel ( ) const [inline]

Returns:: the kernel of the matrix, also called its null-space. The columns of the returned matrix will form a basis of the kernel.

Note:: If the kernel has dimension zero, then the returned matrix is a column-vector filled with zeros.; This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Example:

Output:

See also:: image()

Definition at line 174 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      return internal::kernel_retval<FullPivLU>(*this);
    }

template<typename _MatrixType >

const MatrixType& Eigen::FullPivLU< _MatrixType >::matrixLU ( ) const [inline]

Returns:: the LU decomposition matrix: the upper-triangular part is U, the unit-lower-triangular part is L (at least for square matrices; in the non-square case, special care is needed, see the documentation of class FullPivLU).

See also:: matrixL(), matrixU()

Definition at line 116 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      return m_lu;
    }

template<typename _MatrixType >

RealScalar Eigen::FullPivLU< _MatrixType >::maxPivot ( ) const [inline]

Returns:: the absolute value of the biggest pivot, i.e. the biggest diagonal coefficient of U.

Definition at line 138 of file FullPivLU.h.

{ return m_maxpivot; }

template<typename _MatrixType >

Index Eigen::FullPivLU< _MatrixType >::nonzeroPivots ( ) const [inline]

Returns:: the number of nonzero pivots in the LU decomposition. Here nonzero is meant in the exact sense, not in a fuzzy sense. So that notion isn't really intrinsically interesting, but it is still useful when implementing algorithms.

See also:: rank()

Definition at line 129 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      return m_nonzero_pivots;
    }

template<typename _MatrixType >

const PermutationPType& Eigen::FullPivLU< _MatrixType >::permutationP ( ) const [inline]

Returns:: the permutation matrix P

See also:: permutationQ()

Definition at line 144 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      return m_p;
    }

template<typename _MatrixType >

const PermutationQType& Eigen::FullPivLU< _MatrixType >::permutationQ ( ) const [inline]

Returns:: the permutation matrix Q

See also:: permutationP()

Definition at line 154 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      return m_q;
    }

template<typename _MatrixType >

Index Eigen::FullPivLU< _MatrixType >::rank ( ) const [inline]

Returns:: the rank of the matrix of which *this is the LU decomposition.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 308 of file FullPivLU.h.

    {
      using std::abs;
      eigen_assert(m_isInitialized && "LU is not initialized.");
      RealScalar premultiplied_threshold = abs(m_maxpivot) * threshold();
      Index result = 0;
      for(Index i = 0; i < m_nonzero_pivots; ++i)
        result += (abs(m_lu.coeff(i,i)) > premultiplied_threshold);
      return result;
    }

template<typename MatrixType >

MatrixType Eigen::FullPivLU< MatrixType >::reconstructedMatrix ( ) const

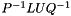Returns:: the matrix represented by the decomposition, i.e., it returns the product: $P^{-1} L U Q^{-1}$ . This function is provided for debug purposes.

Definition at line 562 of file FullPivLU.h.

{
  eigen_assert(m_isInitialized && "LU is not initialized.");
  const Index smalldim = (std::min)(m_lu.rows(), m_lu.cols());
  // LU
  MatrixType res(m_lu.rows(),m_lu.cols());
  // FIXME the .toDenseMatrix() should not be needed...
  res = m_lu.leftCols(smalldim)
            .template triangularView<UnitLower>().toDenseMatrix()
      * m_lu.topRows(smalldim)
            .template triangularView<Upper>().toDenseMatrix();

  // P^{-1}(LU)
  res = m_p.inverse() * res;

  // (P^{-1}LU)Q^{-1}
  res = res * m_q.inverse();

  return res;
}

template<typename _MatrixType >

Index Eigen::FullPivLU< _MatrixType >::rows ( void ) const [inline]

Returns:: the number of rows.

See also:: cols(), RowsAtCompileTime

Reimplemented from Eigen::EigenBase< FullPivLU< _MatrixType > >.

Definition at line 385 of file FullPivLU.h.

{ return m_lu.rows(); }

template<typename _MatrixType >

FullPivLU& Eigen::FullPivLU< _MatrixType >::setThreshold ( const RealScalar & threshold ) [inline]

Allows to prescribe a threshold to be used by certain methods, such as rank(), who need to determine when pivots are to be considered nonzero. This is not used for the LU decomposition itself.

When it needs to get the threshold value, Eigen calls threshold(). By default, this uses a formula to automatically determine a reasonable threshold. Once you have called the present method setThreshold(const RealScalar&), your value is used instead.

Parameters:

threshold The new value to use as the threshold.

A pivot will be considered nonzero if its absolute value is strictly greater than 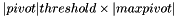$\vert pivot \vert \leqslant threshold \times \vert maxpivot \vert$ where maxpivot is the biggest pivot.

If you want to come back to the default behavior, call setThreshold(Default_t)

Definition at line 268 of file FullPivLU.h.

    {
      m_usePrescribedThreshold = true;
      m_prescribedThreshold = threshold;
      return *this;
    }

template<typename _MatrixType >

FullPivLU& Eigen::FullPivLU< _MatrixType >::setThreshold ( Default_t ) [inline]

Allows to come back to the default behavior, letting Eigen use its default formula for determining the threshold.

You should pass the special object Eigen::Default as parameter here.

 lu.setThreshold(Eigen::Default);

See the documentation of setThreshold(const RealScalar&).

Definition at line 283 of file FullPivLU.h.

    {
      m_usePrescribedThreshold = false;
      return *this;
    }

template<typename _MatrixType >

template<typename Rhs >

const Solve<FullPivLU, Rhs> Eigen::FullPivLU< _MatrixType >::solve ( const MatrixBase< Rhs > & b ) const [inline]

Returns:: a solution x to the equation Ax=b, where A is the matrix of which *this is the LU decomposition.

Parameters:

b	the right-hand-side of the equation to solve. Can be a vector or a matrix, the only requirement in order for the equation to make sense is that b.rows()==A.rows(), where A is the matrix of which *this is the LU decomposition.

Returns:: a solution.

Example:

Output:

See also:: TriangularView::solve(), kernel(), inverse()

Reimplemented from Eigen::SolverBase< FullPivLU< _MatrixType > >.

Definition at line 228 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      return Solve<FullPivLU, Rhs>(*this, b.derived());
    }

template<typename _MatrixType >

RealScalar Eigen::FullPivLU< _MatrixType >::threshold ( ) const [inline]

Returns the threshold that will be used by certain methods such as rank().

See the documentation of setThreshold(const RealScalar&).

Definition at line 293 of file FullPivLU.h.

    {
      eigen_assert(m_isInitialized || m_usePrescribedThreshold);
      return m_usePrescribedThreshold ? m_prescribedThreshold
      // this formula comes from experimenting (see "LU precision tuning" thread on the list)
      // and turns out to be identical to Higham's formula used already in LDLt.
                                      : NumTraits<Scalar>::epsilon() * m_lu.diagonalSize();
    }

Member Data Documentation

template<typename _MatrixType >

IntRowVectorType Eigen::FullPivLU< _MatrixType >::m_colsTranspositions [protected]

Definition at line 411 of file FullPivLU.h.

template<typename _MatrixType >

Index Eigen::FullPivLU< _MatrixType >::m_det_pq [protected]

Definition at line 412 of file FullPivLU.h.

template<typename _MatrixType >

bool Eigen::FullPivLU< _MatrixType >::m_isInitialized [protected]

Definition at line 414 of file FullPivLU.h.

template<typename _MatrixType >

MatrixType Eigen::FullPivLU< _MatrixType >::m_lu [protected]

Definition at line 407 of file FullPivLU.h.

template<typename _MatrixType >

RealScalar Eigen::FullPivLU< _MatrixType >::m_maxpivot [protected]

Definition at line 413 of file FullPivLU.h.

template<typename _MatrixType >

Index Eigen::FullPivLU< _MatrixType >::m_nonzero_pivots [protected]

Definition at line 412 of file FullPivLU.h.

template<typename _MatrixType >

PermutationPType Eigen::FullPivLU< _MatrixType >::m_p [protected]

Definition at line 408 of file FullPivLU.h.

template<typename _MatrixType >

RealScalar Eigen::FullPivLU< _MatrixType >::m_prescribedThreshold [protected]

Definition at line 413 of file FullPivLU.h.

template<typename _MatrixType >

PermutationQType Eigen::FullPivLU< _MatrixType >::m_q [protected]

Definition at line 409 of file FullPivLU.h.

template<typename _MatrixType >

IntColVectorType Eigen::FullPivLU< _MatrixType >::m_rowsTranspositions [protected]

Definition at line 410 of file FullPivLU.h.

template<typename _MatrixType >

bool Eigen::FullPivLU< _MatrixType >::m_usePrescribedThreshold [protected]

Definition at line 414 of file FullPivLU.h.

The documentation for this class was generated from the following file:

FullPivLU.h

Public Types

Public Member Functions

Protected Member Functions

Static Protected Member Functions

Protected Attributes

Detailed Description

template<typename _MatrixType> class Eigen::FullPivLU< _MatrixType >

Member Typedef Documentation

Member Enumeration Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<typename _MatrixType>
class Eigen::FullPivLU< _MatrixType >