MOAB  4.9.3pre
Public Types | Public Member Functions | Static Public Member Functions | Protected Attributes | Private Types | Friends
Eigen::AngleAxis< _Scalar > Class Template Reference
Geometry_Module

Represents a 3D rotation as a rotation angle around an arbitrary 3D axis. More...

#include <AngleAxis.h>

Inheritance diagram for Eigen::AngleAxis< _Scalar >:
Inheritance graph
[legend]
Collaboration diagram for Eigen::AngleAxis< _Scalar >:
Collaboration graph
[legend]

List of all members.

Public Types

enum  { Dim = 3 }
typedef _Scalar Scalar
typedef Matrix< Scalar, 3, 3 > Matrix3
typedef Matrix< Scalar, 3, 1 > Vector3
typedef Quaternion< Scalar > QuaternionType

Public Member Functions

 AngleAxis ()
template<typename Derived >
 AngleAxis (const Scalar &angle, const MatrixBase< Derived > &axis)
template<typename QuatDerived >
 AngleAxis (const QuaternionBase< QuatDerived > &q)
template<typename Derived >
 AngleAxis (const MatrixBase< Derived > &m)
Scalar angle () const
Scalar & angle ()
const Vector3 & axis () const
Vector3 & axis ()
QuaternionType operator* (const AngleAxis &other) const
QuaternionType operator* (const QuaternionType &other) const
AngleAxis inverse () const
template<class QuatDerived >
AngleAxis & operator= (const QuaternionBase< QuatDerived > &q)
template<typename Derived >
AngleAxis & operator= (const MatrixBase< Derived > &m)
template<typename Derived >
AngleAxis & fromRotationMatrix (const MatrixBase< Derived > &m)
 Sets *this from a 3x3 rotation matrix.
Matrix3 toRotationMatrix (void) const
template<typename NewScalarType >
internal::cast_return_type
< AngleAxis, AngleAxis
< NewScalarType > >::type 		cast () const
template<typename OtherScalarType >
 AngleAxis (const AngleAxis< OtherScalarType > &other)
bool isApprox (const AngleAxis &other, const typename NumTraits< Scalar >::Real &prec=NumTraits< Scalar >::dummy_precision()) const

Static Public Member Functions

static const AngleAxis Identity ()

Protected Attributes

Vector3 m_axis
Scalar m_angle

Private Types

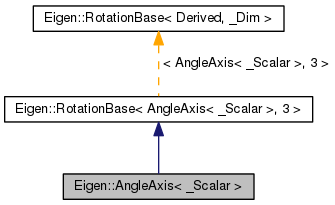
typedef RotationBase
< AngleAxis< _Scalar >, 3 > 		Base

Friends

QuaternionType operator* (const QuaternionType &a, const AngleAxis &b)

Detailed Description

template<typename _Scalar>
class Eigen::AngleAxis< _Scalar >

Represents a 3D rotation as a rotation angle around an arbitrary 3D axis.

Parameters:
_Scalarthe scalar type, i.e., the type of the coefficients.
Warning:
When setting up an AngleAxis object, the axis vector must be normalized.

The following two typedefs are provided for convenience:

  • AngleAxisf for float
  • AngleAxisd for double

Combined with MatrixBase::Unit{X,Y,Z}, AngleAxis can be used to easily mimic Euler-angles. Here is an example: 

 Output: 


Note:
This class is not aimed to be used to store a rotation transformation, but rather to make easier the creation of other rotation (Quaternion, rotation Matrix) and transformation objects.


See also:
class Quaternion, class Transform, MatrixBase::UnitX() 



Definition at line 49 of file AngleAxis.h.


Member Typedef Documentation








template<typename _Scalar> 

      

        

          typedef RotationBase<AngleAxis<_Scalar>,3> Eigen::AngleAxis< _Scalar >::Base [private]
        

      







Definition at line 51 of file AngleAxis.h.













template<typename _Scalar> 

      

        

          typedef Matrix<Scalar,3,3> Eigen::AngleAxis< _Scalar >::Matrix3
        

      







Definition at line 60 of file AngleAxis.h.













template<typename _Scalar> 

      

        

          typedef Quaternion<Scalar> Eigen::AngleAxis< _Scalar >::QuaternionType
        

      







Definition at line 62 of file AngleAxis.h.













template<typename _Scalar> 

      

        

          typedef _Scalar Eigen::AngleAxis< _Scalar >::Scalar
        

      






the scalar type of the coefficients 



Reimplemented from Eigen::RotationBase< AngleAxis< _Scalar >, 3 >.



Definition at line 59 of file AngleAxis.h.













template<typename _Scalar> 

      

        

          typedef Matrix<Scalar,3,1> Eigen::AngleAxis< _Scalar >::Vector3
        

      







Definition at line 61 of file AngleAxis.h.







Member Enumeration Documentation








template<typename _Scalar> 

      

        

          anonymous enum
        

      






Enumerator: 


Dim 










Definition at line 57 of file AngleAxis.h.


{ Dim = 3 };







Constructor & Destructor Documentation








template<typename _Scalar> 

      

        

          Eigen::AngleAxis< _Scalar >::AngleAxis 
          (
          )
           [inline]
        

      






Default constructor without initialization. 



Definition at line 72 of file AngleAxis.h.


{}













template<typename _Scalar> 



template<typename Derived > 

      

        

          Eigen::AngleAxis< _Scalar >::AngleAxis 
          (
          const Scalar & 
          angle, 
        

        

          
          
          const MatrixBase< Derived > & 
          axis 
        

        

          
          )
           [inline]
        

      






Constructs and initialize the angle-axis rotation from an angle in radian and an axis which must be normalized.


Warning:
If the axis vector is not normalized, then the angle-axis object represents an invalid rotation. 



Definition at line 79 of file AngleAxis.h.


: m_axis(axis), m_angle(angle) {}













template<typename _Scalar> 



template<typename QuatDerived > 

      

        

          Eigen::AngleAxis< _Scalar >::AngleAxis 
          (
          const QuaternionBase< QuatDerived > & 
          q)
           [inline, explicit]
        

      






Constructs and initialize the angle-axis rotation from a quaternion q. This function implicitly normalizes the quaternion q. 



Definition at line 83 of file AngleAxis.h.


{ *this = q; }













template<typename _Scalar> 



template<typename Derived > 

      

        

          Eigen::AngleAxis< _Scalar >::AngleAxis 
          (
          const MatrixBase< Derived > & 
          m)
           [inline, explicit]
        

      






Constructs and initialize the angle-axis rotation from a 3x3 rotation matrix. 



Definition at line 86 of file AngleAxis.h.


{ *this = m; }













template<typename _Scalar> 



template<typename OtherScalarType > 

      

        

          Eigen::AngleAxis< _Scalar >::AngleAxis 
          (
          const AngleAxis< OtherScalarType > & 
          other)
           [inline, explicit]
        

      






Copy constructor with scalar type conversion 



Definition at line 137 of file AngleAxis.h.


  {
    m_axis = other.axis().template cast<Scalar>();
    m_angle = Scalar(other.angle());
  }







Member Function Documentation








template<typename _Scalar> 

      

        

          Scalar Eigen::AngleAxis< _Scalar >::angle 
          (
          )
           const [inline]
        

      






Returns:
the value of the rotation angle in radian 



Definition at line 89 of file AngleAxis.h.


{ return m_angle; }













template<typename _Scalar> 

      

        

          Scalar& Eigen::AngleAxis< _Scalar >::angle 
          (
          )
           [inline]
        

      






Returns:
a read-write reference to the stored angle in radian 



Definition at line 91 of file AngleAxis.h.


{ return m_angle; }













template<typename _Scalar> 

      

        

          const Vector3& Eigen::AngleAxis< _Scalar >::axis 
          (
          )
           const [inline]
        

      






Returns:
the rotation axis 



Definition at line 94 of file AngleAxis.h.


{ return m_axis; }













template<typename _Scalar> 

      

        

          Vector3& Eigen::AngleAxis< _Scalar >::axis 
          (
          )
           [inline]
        

      






Returns:
a read-write reference to the stored rotation axis.


Warning:
The rotation axis must remain a unit vector. 



Definition at line 99 of file AngleAxis.h.


{ return m_axis; }













template<typename _Scalar> 



template<typename NewScalarType > 

      

        

          internal::cast_return_type<AngleAxis,AngleAxis<NewScalarType> >::type Eigen::AngleAxis< _Scalar >::cast 
          (
          )
           const [inline]
        

      






Returns:
*this with scalar type casted to NewScalarType 


Note that if NewScalarType is equal to the current scalar type of *this then this function smartly returns a const reference to *this. 



Definition at line 132 of file AngleAxis.h.


  { return typename internal::cast_return_type<AngleAxis,AngleAxis<NewScalarType> >::type(*this); }













template<typename Scalar > 



template<typename Derived > 

      

        

          AngleAxis< Scalar > & Eigen::AngleAxis< Scalar >::fromRotationMatrix 
          (
          const MatrixBase< Derived > & 
          m)
          
        

      







Sets *this from a 3x3 rotation matrix. 



Definition at line 202 of file AngleAxis.h.


{
  return *this = QuaternionType(mat);
}













template<typename _Scalar> 

      

        

          static const AngleAxis Eigen::AngleAxis< _Scalar >::Identity 
          (
          )
           [inline, static]
        

      







Definition at line 143 of file AngleAxis.h.


{ return AngleAxis(Scalar(0), Vector3::UnitX()); }













template<typename _Scalar> 

      

        

          AngleAxis Eigen::AngleAxis< _Scalar >::inverse 
          (
          )
           const [inline]
        

      






Returns:
the inverse rotation, i.e., an angle-axis with opposite rotation angle 



Reimplemented from Eigen::RotationBase< AngleAxis< _Scalar >, 3 >.



Definition at line 114 of file AngleAxis.h.


  { return AngleAxis(-m_angle, m_axis); }













template<typename _Scalar> 

      

        

          bool Eigen::AngleAxis< _Scalar >::isApprox 
          (
          const AngleAxis< _Scalar > & 
          other, 
        

        

          
          
          const typename NumTraits< Scalar >::Real & 
          prec = NumTraits<Scalar>::dummy_precision() 
        

        

          
          )
           const [inline]
        

      






Returns:
true if *this is approximately equal to other, within the precision determined by prec.


See also:
MatrixBase::isApprox() 



Definition at line 149 of file AngleAxis.h.


  { return m_axis.isApprox(other.m_axis, prec) && internal::isApprox(m_angle,other.m_angle, prec); }













template<typename _Scalar> 

      

        

          QuaternionType Eigen::AngleAxis< _Scalar >::operator* 
          (
          const AngleAxis< _Scalar > & 
          other)
           const [inline]
        

      






Concatenates two rotations 



Definition at line 102 of file AngleAxis.h.


  { return QuaternionType(*this) * QuaternionType(other); }













template<typename _Scalar> 

      

        

          QuaternionType Eigen::AngleAxis< _Scalar >::operator* 
          (
          const QuaternionType & 
          other)
           const [inline]
        

      






Concatenates two rotations 



Definition at line 106 of file AngleAxis.h.


  { return QuaternionType(*this) * other; }













template<typename Scalar > 



template<typename QuatDerived > 

      

        

          AngleAxis< Scalar > & Eigen::AngleAxis< Scalar >::operator= 
          (
          const QuaternionBase< QuatDerived > & 
          q)
          
        

      






Set *this from a unit quaternion. The resulting axis is normalized.


This function implicitly normalizes the quaternion q. 



Definition at line 167 of file AngleAxis.h.


{
  using std::atan2;
  Scalar n = q.vec().norm();
  if(n<NumTraits<Scalar>::epsilon())
    n = q.vec().stableNorm();
  if (n > Scalar(0))
  {
    m_angle = Scalar(2)*atan2(n, q.w());
    m_axis  = q.vec() / n;
  }
  else
  {
    m_angle = Scalar(0);
    m_axis << Scalar(1), Scalar(0), Scalar(0);
  }
  return *this;
}













template<typename Scalar > 



template<typename Derived > 

      

        

          AngleAxis< Scalar > & Eigen::AngleAxis< Scalar >::operator= 
          (
          const MatrixBase< Derived > & 
          mat)
          
        

      






Set *this from a 3x3 rotation matrix mat. 



Definition at line 190 of file AngleAxis.h.


{
  // Since a direct conversion would not be really faster,
  // let's use the robust Quaternion implementation:
  return *this = QuaternionType(mat);
}













template<typename Scalar > 

      

        

          AngleAxis< Scalar >::Matrix3 Eigen::AngleAxis< Scalar >::toRotationMatrix 
          (
          void 
          )
           const
        

      






Constructs and 


Returns:
an equivalent 3x3 rotation matrix. 



Reimplemented from Eigen::RotationBase< AngleAxis< _Scalar >, 3 >.



Definition at line 211 of file AngleAxis.h.


{
  using std::sin;
  using std::cos;
  Matrix3 res;
  Vector3 sin_axis  = sin(m_angle) * m_axis;
  Scalar c = cos(m_angle);
  Vector3 cos1_axis = (Scalar(1)-c) * m_axis;

  Scalar tmp;
  tmp = cos1_axis.x() * m_axis.y();
  res.coeffRef(0,1) = tmp - sin_axis.z();
  res.coeffRef(1,0) = tmp + sin_axis.z();

  tmp = cos1_axis.x() * m_axis.z();
  res.coeffRef(0,2) = tmp + sin_axis.y();
  res.coeffRef(2,0) = tmp - sin_axis.y();

  tmp = cos1_axis.y() * m_axis.z();
  res.coeffRef(1,2) = tmp - sin_axis.x();
  res.coeffRef(2,1) = tmp + sin_axis.x();

  res.diagonal() = (cos1_axis.cwiseProduct(m_axis)).array() + c;

  return res;
}







Friends And Related Function Documentation








template<typename _Scalar> 

      

        

          QuaternionType operator* 
          (
          const QuaternionType & 
          a, 
        

        

          
          
          const AngleAxis< _Scalar > & 
          b 
        

        

          
          )
           [friend]
        

      






Concatenates two rotations 



Definition at line 110 of file AngleAxis.h.


  { return a * QuaternionType(b); }







Member Data Documentation








template<typename _Scalar> 

      

        

          Scalar Eigen::AngleAxis< _Scalar >::m_angle [protected]
        

      







Definition at line 67 of file AngleAxis.h.













template<typename _Scalar> 

      

        

          Vector3 Eigen::AngleAxis< _Scalar >::m_axis [protected]
        

      







Definition at line 66 of file AngleAxis.h.







The documentation for this class was generated from the following file:







 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Defines