Collaboration diagram for Geometry_Module:

Classes
class	Eigen::Map< const Quaternion< _Scalar >, _Options >
	Quaternion expression mapping a constant memory buffer. More...
class	Eigen::Map< Quaternion< _Scalar >, _Options >
	Expression of a quaternion from a memory buffer. More...
class	Eigen::AlignedBox< _Scalar, _AmbientDim >
	An axis aligned box. More...
class	Eigen::AngleAxis< _Scalar >
	Represents a 3D rotation as a rotation angle around an arbitrary 3D axis. More...
class	Eigen::Homogeneous< MatrixType, _Direction >
	Expression of one (or a set of) homogeneous vector(s) More...
class	Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >
	A hyperplane. More...
class	Eigen::ParametrizedLine< _Scalar, _AmbientDim, _Options >
	A parametrized line. More...
class	Eigen::QuaternionBase< Derived >
	Base class for quaternion expressions. More...
class	Eigen::Quaternion< _Scalar, _Options >
	The quaternion class used to represent 3D orientations and rotations. More...
class	Eigen::Rotation2D< _Scalar >
	Represents a rotation/orientation in a 2 dimensional space. More...
class	Scaling
	Represents a generic uniform scaling transformation. More...
class	Eigen::Transform< _Scalar, _Dim, _Mode, _Options >
	Represents an homogeneous transformation in a N dimensional space. More...
class	Eigen::Translation< _Scalar, _Dim >
	Represents a translation transformation. More...
Modules
	Global aligned box typedefs
Typedefs
typedef AngleAxis< float >	Eigen::AngleAxisf
typedef AngleAxis< double >	Eigen::AngleAxisd
typedef Quaternion< float >	Eigen::Quaternionf
typedef Quaternion< double >	Eigen::Quaterniond
typedef Map< Quaternion< float >, 0 >	Eigen::QuaternionMapf
typedef Map< Quaternion < double >, 0 >	Eigen::QuaternionMapd
typedef Map< Quaternion< float > , Aligned >	Eigen::QuaternionMapAlignedf
typedef Map< Quaternion < double >, Aligned >	Eigen::QuaternionMapAlignedd
typedef Rotation2D< float >	Eigen::Rotation2Df
typedef Rotation2D< double >	Eigen::Rotation2Dd
typedef DiagonalMatrix< float, 2 >	Eigen::AlignedScaling2f
typedef DiagonalMatrix< double, 2 >	Eigen::AlignedScaling2d
typedef DiagonalMatrix< float, 3 >	Eigen::AlignedScaling3f
typedef DiagonalMatrix< double, 3 >	Eigen::AlignedScaling3d
typedef Transform< float, 2, Isometry >	Eigen::Isometry2f
typedef Transform< float, 3, Isometry >	Eigen::Isometry3f
typedef Transform< double, 2, Isometry >	Eigen::Isometry2d
typedef Transform< double, 3, Isometry >	Eigen::Isometry3d
typedef Transform< float, 2, Affine >	Eigen::Affine2f
typedef Transform< float, 3, Affine >	Eigen::Affine3f
typedef Transform< double, 2, Affine >	Eigen::Affine2d
typedef Transform< double, 3, Affine >	Eigen::Affine3d
typedef Transform< float, 2, AffineCompact >	Eigen::AffineCompact2f
typedef Transform< float, 3, AffineCompact >	Eigen::AffineCompact3f
typedef Transform< double, 2, AffineCompact >	Eigen::AffineCompact2d
typedef Transform< double, 3, AffineCompact >	Eigen::AffineCompact3d
typedef Transform< float, 2, Projective >	Eigen::Projective2f
typedef Transform< float, 3, Projective >	Eigen::Projective3f
typedef Transform< double, 2, Projective >	Eigen::Projective2d
typedef Transform< double, 3, Projective >	Eigen::Projective3d
typedef Translation< float, 2 >	Eigen::Translation2f
typedef Translation< double, 2 >	Eigen::Translation2d
typedef Translation< float, 3 >	Eigen::Translation3f
typedef Translation< double, 3 >	Eigen::Translation3d
Functions
static UniformScaling< float >	Eigen::Scaling (float s)
static UniformScaling< double >	Eigen::Scaling (double s)
template<typename RealScalar >
static UniformScaling < std::complex< RealScalar > >	Eigen::Scaling (const std::complex< RealScalar > &s)
template<typename Scalar >
static DiagonalMatrix< Scalar, 2 >	Eigen::Scaling (const Scalar &sx, const Scalar &sy)
template<typename Scalar >
static DiagonalMatrix< Scalar, 3 >	Eigen::Scaling (const Scalar &sx, const Scalar &sy, const Scalar &sz)
template<typename Derived >
static const DiagonalWrapper < const Derived >	Eigen::Scaling (const MatrixBase< Derived > &coeffs)
template<typename Derived , typename OtherDerived >
internal::umeyama_transform_matrix_type < Derived, OtherDerived > ::type	Eigen::umeyama (const MatrixBase< Derived > &src, const MatrixBase< OtherDerived > &dst, bool with_scaling=true)
	Returns the transformation between two point sets.
Matrix< Scalar, 3, 1 >	Eigen::MatrixBase< Derived >::eulerAngles (Index a0, Index a1, Index a2) const
HomogeneousReturnType	Eigen::MatrixBase< Derived >::homogeneous () const
HomogeneousReturnType	Eigen::VectorwiseOp< ExpressionType, Direction >::homogeneous () const
const HNormalizedReturnType	Eigen::MatrixBase< Derived >::hnormalized () const
const HNormalizedReturnType	Eigen::VectorwiseOp< ExpressionType, Direction >::hnormalized () const
template<typename OtherDerived >
EIGEN_DEVICE_FUNC cross_product_return_type < OtherDerived >::type	Eigen::MatrixBase< Derived >::cross (const MatrixBase< OtherDerived > &other) const
template<typename OtherDerived >
EIGEN_DEVICE_FUNC PlainObject	Eigen::MatrixBase< Derived >::cross3 (const MatrixBase< OtherDerived > &other) const
template<typename OtherDerived >
EIGEN_DEVICE_FUNC const CrossReturnType	Eigen::VectorwiseOp< ExpressionType, Direction >::cross (const MatrixBase< OtherDerived > &other) const
EIGEN_DEVICE_FUNC PlainObject	Eigen::MatrixBase< Derived >::unitOrthogonal (void) const
ScalarMultipleReturnType	Eigen::MatrixBase< Derived >::operator* (const UniformScaling< Scalar > &s) const

Typedef Documentation

typedef Transform<double,2,Affine> Eigen::Affine2d

Definition at line 692 of file Transform.h.

typedef Transform<float,2,Affine> Eigen::Affine2f

Definition at line 688 of file Transform.h.

typedef Transform<double,3,Affine> Eigen::Affine3d

Definition at line 694 of file Transform.h.

typedef Transform<float,3,Affine> Eigen::Affine3f

Definition at line 690 of file Transform.h.

typedef Transform<double,2,AffineCompact> Eigen::AffineCompact2d

Definition at line 701 of file Transform.h.

typedef Transform<float,2,AffineCompact> Eigen::AffineCompact2f

Definition at line 697 of file Transform.h.

typedef Transform<double,3,AffineCompact> Eigen::AffineCompact3d

Definition at line 703 of file Transform.h.

typedef Transform<float,3,AffineCompact> Eigen::AffineCompact3f

Definition at line 699 of file Transform.h.

typedef DiagonalMatrix<double,2> Eigen::AlignedScaling2d

Deprecated:

Definition at line 145 of file Scaling.h.

typedef DiagonalMatrix<float, 2> Eigen::AlignedScaling2f

Deprecated:

Definition at line 143 of file Scaling.h.

typedef DiagonalMatrix<double,3> Eigen::AlignedScaling3d

Deprecated:

Definition at line 149 of file Scaling.h.

typedef DiagonalMatrix<float, 3> Eigen::AlignedScaling3f

Deprecated:

Definition at line 147 of file Scaling.h.

typedef AngleAxis<double> Eigen::AngleAxisd

double precision angle-axis type

Definition at line 158 of file AngleAxis.h.

typedef AngleAxis<float> Eigen::AngleAxisf

single precision angle-axis type

Definition at line 155 of file AngleAxis.h.

typedef Transform<double,2,Isometry> Eigen::Isometry2d

Definition at line 683 of file Transform.h.

typedef Transform<float,2,Isometry> Eigen::Isometry2f

Definition at line 679 of file Transform.h.

typedef Transform<double,3,Isometry> Eigen::Isometry3d

Definition at line 685 of file Transform.h.

typedef Transform<float,3,Isometry> Eigen::Isometry3f

Definition at line 681 of file Transform.h.

typedef Transform<double,2,Projective> Eigen::Projective2d

Definition at line 710 of file Transform.h.

typedef Transform<float,2,Projective> Eigen::Projective2f

Definition at line 706 of file Transform.h.

typedef Transform<double,3,Projective> Eigen::Projective3d

Definition at line 712 of file Transform.h.

typedef Transform<float,3,Projective> Eigen::Projective3f

Definition at line 708 of file Transform.h.

typedef Quaternion<double> Eigen::Quaterniond

double precision quaternion type

Definition at line 303 of file Quaternion.h.

typedef Quaternion<float> Eigen::Quaternionf

single precision quaternion type

Definition at line 300 of file Quaternion.h.

typedef Map<Quaternion<double>, Aligned> Eigen::QuaternionMapAlignedd

Map a 16-byte aligned array of double precision scalars as a quaternion

Definition at line 415 of file Quaternion.h.

typedef Map<Quaternion<float>, Aligned> Eigen::QuaternionMapAlignedf

Map a 16-byte aligned array of single precision scalars as a quaternion

Definition at line 412 of file Quaternion.h.

typedef Map<Quaternion<double>, 0> Eigen::QuaternionMapd

Map an unaligned array of double precision scalars as a quaternion

Definition at line 409 of file Quaternion.h.

typedef Map<Quaternion<float>, 0> Eigen::QuaternionMapf

Map an unaligned array of single precision scalars as a quaternion

Definition at line 406 of file Quaternion.h.

typedef Rotation2D<double> Eigen::Rotation2Dd

double precision 2D rotation type

Definition at line 168 of file Rotation2D.h.

typedef Rotation2D<float> Eigen::Rotation2Df

single precision 2D rotation type

Definition at line 165 of file Rotation2D.h.

typedef Translation<double,2> Eigen::Translation2d

Definition at line 173 of file Translation.h.

typedef Translation<float, 2> Eigen::Translation2f

Definition at line 172 of file Translation.h.

typedef Translation<double,3> Eigen::Translation3d

Definition at line 175 of file Translation.h.

typedef Translation<float, 3> Eigen::Translation3f

Definition at line 174 of file Translation.h.

Function Documentation

template<typename Derived >

template<typename OtherDerived >

MatrixBase< Derived >::template cross_product_return_type< OtherDerived >::type Eigen::MatrixBase< Derived >::cross ( const MatrixBase< OtherDerived > & other ) const [inline]

Returns:: the cross product of *this and other

Here is a very good explanation of cross-product: http://xkcd.com/199/

With complex numbers, the cross product is implemented as 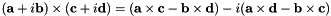$(\mathbf{a}+i\mathbf{b}) \times (\mathbf{c}+i\mathbf{d}) = (\mathbf{a} \times \mathbf{c} - \mathbf{b} \times \mathbf{d}) - i(\mathbf{a} \times \mathbf{d} - \mathbf{b} \times \mathbf{c})$

See also:: MatrixBase::cross3()

Definition at line 34 of file OrthoMethods.h.

{
  EIGEN_STATIC_ASSERT_VECTOR_SPECIFIC_SIZE(Derived,3)
  EIGEN_STATIC_ASSERT_VECTOR_SPECIFIC_SIZE(OtherDerived,3)

  // Note that there is no need for an expression here since the compiler
  // optimize such a small temporary very well (even within a complex expression)
  typename internal::nested_eval<Derived,2>::type lhs(derived());
  typename internal::nested_eval<OtherDerived,2>::type rhs(other.derived());
  return typename cross_product_return_type<OtherDerived>::type(
    numext::conj(lhs.coeff(1) * rhs.coeff(2) - lhs.coeff(2) * rhs.coeff(1)),
    numext::conj(lhs.coeff(2) * rhs.coeff(0) - lhs.coeff(0) * rhs.coeff(2)),
    numext::conj(lhs.coeff(0) * rhs.coeff(1) - lhs.coeff(1) * rhs.coeff(0))
  );
}

template<typename ExpressionType , int Direction>

template<typename OtherDerived >

const VectorwiseOp< ExpressionType, Direction >::CrossReturnType Eigen::VectorwiseOp< ExpressionType, Direction >::cross ( const MatrixBase< OtherDerived > & other ) const

Returns:: a matrix expression of the cross product of each column or row of the referenced expression with the other vector.

The referenced matrix must have one dimension equal to 3. The result matrix has the same dimensions than the referenced one.

See also:: MatrixBase::cross()

Definition at line 109 of file OrthoMethods.h.

{
  EIGEN_STATIC_ASSERT_VECTOR_SPECIFIC_SIZE(OtherDerived,3)
  EIGEN_STATIC_ASSERT((internal::is_same<Scalar, typename OtherDerived::Scalar>::value),
    YOU_MIXED_DIFFERENT_NUMERIC_TYPES__YOU_NEED_TO_USE_THE_CAST_METHOD_OF_MATRIXBASE_TO_CAST_NUMERIC_TYPES_EXPLICITLY)
  
  typename internal::nested_eval<ExpressionType,2>::type mat(_expression());
  typename internal::nested_eval<OtherDerived,2>::type vec(other.derived());

  CrossReturnType res(_expression().rows(),_expression().cols());
  if(Direction==Vertical)
  {
    eigen_assert(CrossReturnType::RowsAtCompileTime==3 && "the matrix must have exactly 3 rows");
    res.row(0) = (mat.row(1) * vec.coeff(2) - mat.row(2) * vec.coeff(1)).conjugate();
    res.row(1) = (mat.row(2) * vec.coeff(0) - mat.row(0) * vec.coeff(2)).conjugate();
    res.row(2) = (mat.row(0) * vec.coeff(1) - mat.row(1) * vec.coeff(0)).conjugate();
  }
  else
  {
    eigen_assert(CrossReturnType::ColsAtCompileTime==3 && "the matrix must have exactly 3 columns");
    res.col(0) = (mat.col(1) * vec.coeff(2) - mat.col(2) * vec.coeff(1)).conjugate();
    res.col(1) = (mat.col(2) * vec.coeff(0) - mat.col(0) * vec.coeff(2)).conjugate();
    res.col(2) = (mat.col(0) * vec.coeff(1) - mat.col(1) * vec.coeff(0)).conjugate();
  }
  return res;
}

template<typename Derived >

template<typename OtherDerived >

MatrixBase< Derived >::PlainObject Eigen::MatrixBase< Derived >::cross3 ( const MatrixBase< OtherDerived > & other ) const [inline]

Returns:: the cross product of *this and other using only the x, y, and z coefficients

The size of *this and other must be four. This function is especially useful when using 4D vectors instead of 3D ones to get advantage of SSE/AltiVec vectorization.

See also:: MatrixBase::cross()

Definition at line 82 of file OrthoMethods.h.

{
  EIGEN_STATIC_ASSERT_VECTOR_SPECIFIC_SIZE(Derived,4)
  EIGEN_STATIC_ASSERT_VECTOR_SPECIFIC_SIZE(OtherDerived,4)

  typedef typename internal::nested_eval<Derived,2>::type DerivedNested;
  typedef typename internal::nested_eval<OtherDerived,2>::type OtherDerivedNested;
  DerivedNested lhs(derived());
  OtherDerivedNested rhs(other.derived());

  return internal::cross3_impl<Architecture::Target,
                        typename internal::remove_all<DerivedNested>::type,
                        typename internal::remove_all<OtherDerivedNested>::type>::run(lhs,rhs);
}

template<typename Derived >

Matrix< typename MatrixBase< Derived >::Scalar, 3, 1 > Eigen::MatrixBase< Derived >::eulerAngles	(	Index	a0,
		Index	a1,
		Index	a2
	)		const `[inline]`

Returns:: the Euler-angles of the rotation matrix *this using the convention defined by the triplet (a0,a1,a2)

Each of the three parameters a0,a1,a2 represents the respective rotation axis as an integer in {0,1,2}. For instance, in:

 Vector3f ea = mat.eulerAngles(2, 0, 2);

"2" represents the z axis and "0" the x axis, etc. The returned angles are such that we have the following equality:

 mat == AngleAxisf(ea[0], Vector3f::UnitZ())
      * AngleAxisf(ea[1], Vector3f::UnitX())
      * AngleAxisf(ea[2], Vector3f::UnitZ());

This corresponds to the right-multiply conventions (with right hand side frames).

The returned angles are in the ranges [0:pi]x[-pi:pi]x[-pi:pi].

See also:: class AngleAxis

Definition at line 37 of file EulerAngles.h.

{
  using std::atan2;
  using std::sin;
  using std::cos;
  /* Implemented from Graphics Gems IV */
  EIGEN_STATIC_ASSERT_MATRIX_SPECIFIC_SIZE(Derived,3,3)

  Matrix<Scalar,3,1> res;
  typedef Matrix<typename Derived::Scalar,2,1> Vector2;

  const Index odd = ((a0+1)%3 == a1) ? 0 : 1;
  const Index i = a0;
  const Index j = (a0 + 1 + odd)%3;
  const Index k = (a0 + 2 - odd)%3;
  
  if (a0==a2)
  {
    res[0] = atan2(coeff(j,i), coeff(k,i));
    if((odd && res[0]<Scalar(0)) || ((!odd) && res[0]>Scalar(0)))
    {
      res[0] = (res[0] > Scalar(0)) ? res[0] - Scalar(EIGEN_PI) : res[0] + Scalar(EIGEN_PI);
      Scalar s2 = Vector2(coeff(j,i), coeff(k,i)).norm();
      res[1] = -atan2(s2, coeff(i,i));
    }
    else
    {
      Scalar s2 = Vector2(coeff(j,i), coeff(k,i)).norm();
      res[1] = atan2(s2, coeff(i,i));
    }
    
    // With a=(0,1,0), we have i=0; j=1; k=2, and after computing the first two angles,
    // we can compute their respective rotation, and apply its inverse to M. Since the result must
    // be a rotation around x, we have:
    //
    //  c2  s1.s2 c1.s2                   1  0   0 
    //  0   c1    -s1       *    M    =   0  c3  s3
    //  -s2 s1.c2 c1.c2                   0 -s3  c3
    //
    //  Thus:  m11.c1 - m21.s1 = c3  &   m12.c1 - m22.s1 = s3
    
    Scalar s1 = sin(res[0]);
    Scalar c1 = cos(res[0]);
    res[2] = atan2(c1*coeff(j,k)-s1*coeff(k,k), c1*coeff(j,j) - s1 * coeff(k,j));
  } 
  else
  {
    res[0] = atan2(coeff(j,k), coeff(k,k));
    Scalar c2 = Vector2(coeff(i,i), coeff(i,j)).norm();
    if((odd && res[0]<Scalar(0)) || ((!odd) && res[0]>Scalar(0))) {
      res[0] = (res[0] > Scalar(0)) ? res[0] - Scalar(EIGEN_PI) : res[0] + Scalar(EIGEN_PI);
      res[1] = atan2(-coeff(i,k), -c2);
    }
    else
      res[1] = atan2(-coeff(i,k), c2);
    Scalar s1 = sin(res[0]);
    Scalar c1 = cos(res[0]);
    res[2] = atan2(s1*coeff(k,i)-c1*coeff(j,i), c1*coeff(j,j) - s1 * coeff(k,j));
  }
  if (!odd)
    res = -res;
  
  return res;
}

template<typename Derived >

const MatrixBase< Derived >::HNormalizedReturnType Eigen::MatrixBase< Derived >::hnormalized ( ) const [inline]

Returns:: an expression of the homogeneous normalized vector of *this

Example:

Output:

See also:: VectorwiseOp::hnormalized()

Definition at line 159 of file Homogeneous.h.

{
  EIGEN_STATIC_ASSERT_VECTOR_ONLY(Derived);
  return ConstStartMinusOne(derived(),0,0,
    ColsAtCompileTime==1?size()-1:1,
    ColsAtCompileTime==1?1:size()-1) / coeff(size()-1);
}

template<typename ExpressionType , int Direction>

const VectorwiseOp< ExpressionType, Direction >::HNormalizedReturnType Eigen::VectorwiseOp< ExpressionType, Direction >::hnormalized ( ) const [inline]

Returns:: an expression of the homogeneous normalized vector of *this

Example:

Output:

See also:: MatrixBase::hnormalized()

Definition at line 177 of file Homogeneous.h.

{
  return HNormalized_Block(_expression(),0,0,
      Direction==Vertical   ? _expression().rows()-1 : _expression().rows(),
      Direction==Horizontal ? _expression().cols()-1 : _expression().cols()).cwiseQuotient(
      Replicate<HNormalized_Factors,
                Direction==Vertical   ? HNormalized_SizeMinusOne : 1,
                Direction==Horizontal ? HNormalized_SizeMinusOne : 1>
        (HNormalized_Factors(_expression(),
          Direction==Vertical    ? _expression().rows()-1:0,
          Direction==Horizontal  ? _expression().cols()-1:0,
          Direction==Vertical    ? 1 : _expression().rows(),
          Direction==Horizontal  ? 1 : _expression().cols()),
         Direction==Vertical   ? _expression().rows()-1 : 1,
         Direction==Horizontal ? _expression().cols()-1 : 1));
}

template<typename Derived >

MatrixBase< Derived >::HomogeneousReturnType Eigen::MatrixBase< Derived >::homogeneous ( ) const [inline]

Returns:: an expression of the equivalent homogeneous vector

Example:

Output:

See also:: VectorwiseOp::homogeneous(), class Homogeneous

Definition at line 128 of file Homogeneous.h.

{
  EIGEN_STATIC_ASSERT_VECTOR_ONLY(Derived);
  return HomogeneousReturnType(derived());
}

template<typename ExpressionType , int Direction>

Homogeneous< ExpressionType, Direction > Eigen::VectorwiseOp< ExpressionType, Direction >::homogeneous ( ) const [inline]

Returns:: a matrix expression of homogeneous column (or row) vectors

Example:

Output:

See also:: MatrixBase::homogeneous(), class Homogeneous

Definition at line 144 of file Homogeneous.h.

{
  return HomogeneousReturnType(_expression());
}

template<typename Derived >

MatrixBase< Derived >::ScalarMultipleReturnType Eigen::MatrixBase< Derived >::operator* ( const UniformScaling< Scalar > & s ) const [inline]

Concatenates a linear transformation matrix and a uniform scaling

Definition at line 114 of file Scaling.h.

{ return derived() * s.factor(); }

static UniformScaling<float> Eigen::Scaling ( float s ) [inline, static]

Constructs a uniform scaling from scale factor s

Definition at line 118 of file Scaling.h.

{ return UniformScaling<float>(s); }

static UniformScaling<double> Eigen::Scaling ( double s ) [inline, static]

Constructs a uniform scaling from scale factor s

Definition at line 120 of file Scaling.h.

{ return UniformScaling<double>(s); }

template<typename RealScalar >

static UniformScaling<std::complex<RealScalar> > Eigen::Scaling ( const std::complex< RealScalar > & s ) [inline, static]

Constructs a uniform scaling from scale factor s

Definition at line 123 of file Scaling.h.

{ return UniformScaling<std::complex<RealScalar> >(s); }

template<typename Scalar >

static DiagonalMatrix<Scalar,2> Eigen::Scaling	(	const Scalar &	sx,
		const Scalar &	sy
	)		`[inline, static]`

Constructs a 2D axis aligned scaling

Definition at line 128 of file Scaling.h.

{ return DiagonalMatrix<Scalar,2>(sx, sy); }

template<typename Scalar >

static DiagonalMatrix<Scalar,3> Eigen::Scaling	(	const Scalar &	sx,
		const Scalar &	sy,
		const Scalar &	sz
	)		`[inline, static]`

Constructs a 3D axis aligned scaling

Definition at line 132 of file Scaling.h.

{ return DiagonalMatrix<Scalar,3>(sx, sy, sz); }

template<typename Derived >

static const DiagonalWrapper<const Derived> Eigen::Scaling ( const MatrixBase< Derived > & coeffs ) [inline, static]

Constructs an axis aligned scaling expression from vector expression coeffs This is an alias for coeffs.asDiagonal()

Definition at line 139 of file Scaling.h.

{ return coeffs.asDiagonal(); }

template<typename Derived , typename OtherDerived >

internal::umeyama_transform_matrix_type<Derived, OtherDerived>::type Eigen::umeyama	(	const MatrixBase< Derived > &	src,
		const MatrixBase< OtherDerived > &	dst,
		bool	with_scaling = `true`
	)

Returns the transformation between two point sets.

The algorithm is based on: "Least-squares estimation of transformation parameters between two point patterns", Shinji Umeyama, PAMI 1991, DOI: 10.1109/34.88573

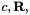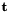It estimates parameters $c, \mathbf{R},$ and $\mathbf{t}$ such that

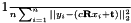
$\begin{align*} \frac{1}{n} \sum_{i=1}^n \vert\vert y_i - (c\mathbf{R}x_i + \mathbf{t}) \vert\vert_2^2 \end{align*}$

is minimized.

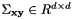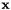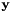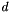The algorithm is based on the analysis of the covariance matrix $\Sigma_{\mathbf{x}\mathbf{y}} \in \mathbb{R}^{d \times d}$ of the input point sets $\mathbf{x}$ and $\mathbf{y}$ where $d$ is corresponding to the dimension (which is typically small). 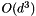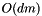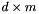The analysis is involving the SVD having a complexity of $O(d^3)$ though the actual computational effort lies in the covariance matrix computation which has an asymptotic lower bound of $O(dm)$ when the input point sets have dimension $d \times m$ .

Currently the method is working only for floating point matrices.

Todo:: Should the return type of umeyama() become a Transform?

Parameters:

src	Source points 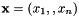$\mathbf{x} = \left( x_1, \hdots, x_n \right)$ .
dst	Destination points 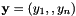$\mathbf{y} = \left( y_1, \hdots, y_n \right)$ .
with_scaling	Sets 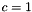when `false` is passed.

Returns:: The homogeneous transformation
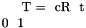
$\begin{align*} T = \begin{bmatrix} c\mathbf{R} & \mathbf{t} \\ \mathbf{0} & 1 \end{bmatrix} \end{align*}$
minimizing the resudiual above. This transformation is always returned as an Eigen::Matrix.

Definition at line 95 of file Umeyama.h.

{
  typedef typename internal::umeyama_transform_matrix_type<Derived, OtherDerived>::type TransformationMatrixType;
  typedef typename internal::traits<TransformationMatrixType>::Scalar Scalar;
  typedef typename NumTraits<Scalar>::Real RealScalar;

  EIGEN_STATIC_ASSERT(!NumTraits<Scalar>::IsComplex, NUMERIC_TYPE_MUST_BE_REAL)
  EIGEN_STATIC_ASSERT((internal::is_same<Scalar, typename internal::traits<OtherDerived>::Scalar>::value),
    YOU_MIXED_DIFFERENT_NUMERIC_TYPES__YOU_NEED_TO_USE_THE_CAST_METHOD_OF_MATRIXBASE_TO_CAST_NUMERIC_TYPES_EXPLICITLY)

  enum { Dimension = EIGEN_SIZE_MIN_PREFER_DYNAMIC(Derived::RowsAtCompileTime, OtherDerived::RowsAtCompileTime) };

  typedef Matrix<Scalar, Dimension, 1> VectorType;
  typedef Matrix<Scalar, Dimension, Dimension> MatrixType;
  typedef typename internal::plain_matrix_type_row_major<Derived>::type RowMajorMatrixType;

  const Index m = src.rows(); // dimension
  const Index n = src.cols(); // number of measurements

  // required for demeaning ...
  const RealScalar one_over_n = RealScalar(1) / static_cast<RealScalar>(n);

  // computation of mean
  const VectorType src_mean = src.rowwise().sum() * one_over_n;
  const VectorType dst_mean = dst.rowwise().sum() * one_over_n;

  // demeaning of src and dst points
  const RowMajorMatrixType src_demean = src.colwise() - src_mean;
  const RowMajorMatrixType dst_demean = dst.colwise() - dst_mean;

  // Eq. (36)-(37)
  const Scalar src_var = src_demean.rowwise().squaredNorm().sum() * one_over_n;

  // Eq. (38)
  const MatrixType sigma = one_over_n * dst_demean * src_demean.transpose();

  JacobiSVD<MatrixType> svd(sigma, ComputeFullU | ComputeFullV);

  // Initialize the resulting transformation with an identity matrix...
  TransformationMatrixType Rt = TransformationMatrixType::Identity(m+1,m+1);

  // Eq. (39)
  VectorType S = VectorType::Ones(m);

  if  ( svd.matrixU().determinant() * svd.matrixV().determinant() < 0 )
    S(m-1) = -1;

  // Eq. (40) and (43)
  Rt.block(0,0,m,m).noalias() = svd.matrixU() * S.asDiagonal() * svd.matrixV().transpose();

  if (with_scaling)
  {
    // Eq. (42)
    const Scalar c = Scalar(1)/src_var * svd.singularValues().dot(S);

    // Eq. (41)
    Rt.col(m).head(m) = dst_mean;
    Rt.col(m).head(m).noalias() -= c*Rt.topLeftCorner(m,m)*src_mean;
    Rt.block(0,0,m,m) *= c;
  }
  else
  {
    Rt.col(m).head(m) = dst_mean;
    Rt.col(m).head(m).noalias() -= Rt.topLeftCorner(m,m)*src_mean;
  }

  return Rt;
}

template<typename Derived >

MatrixBase< Derived >::PlainObject Eigen::MatrixBase< Derived >::unitOrthogonal ( void ) const [inline]

Returns:: a unit vector which is orthogonal to *this

The size of *this must be at least 2. If the size is exactly 2, then the returned vector is a counter clock wise rotation of *this, i.e., (-y,x).normalized().

See also:: cross()

Definition at line 225 of file OrthoMethods.h.

{
  EIGEN_STATIC_ASSERT_VECTOR_ONLY(Derived)
  return internal::unitOrthogonal_selector<Derived>::run(derived());
}

Classes

Modules

Typedefs

Functions

Typedef Documentation

Function Documentation