A hyperplane. More...

#include <Hyperplane.h>

Collaboration diagram for Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >:

Public Types
enum	{ AmbientDimAtCompileTime = _AmbientDim, Options = _Options }
typedef _Scalar	Scalar
typedef NumTraits< Scalar >::Real	RealScalar
typedef Eigen::Index	Index
typedef Matrix< Scalar, AmbientDimAtCompileTime, 1 >	VectorType
typedef Matrix< Scalar, Index(AmbientDimAtCompileTime)==Dynamic?Dynamic:Index(AmbientDimAtCompileTime)+1, 1, Options >	Coefficients
typedef Block< Coefficients, AmbientDimAtCompileTime, 1 >	NormalReturnType
typedef const Block< const Coefficients, AmbientDimAtCompileTime, 1 >	ConstNormalReturnType
Public Member Functions
	Hyperplane ()
template<int OtherOptions>
	Hyperplane (const Hyperplane< Scalar, AmbientDimAtCompileTime, OtherOptions > &other)
	Hyperplane (Index _dim)
	Hyperplane (const VectorType &n, const VectorType &e)
	Hyperplane (const VectorType &n, const Scalar &d)
	Hyperplane (const ParametrizedLine< Scalar, AmbientDimAtCompileTime > &parametrized)
	~Hyperplane ()
Index	dim () const
void	normalize (void)
Scalar	signedDistance (const VectorType &p) const
Scalar	absDistance (const VectorType &p) const
VectorType	projection (const VectorType &p) const
ConstNormalReturnType	normal () const
NormalReturnType	normal ()
const Scalar &	offset () const
Scalar &	offset ()
const Coefficients &	coeffs () const
Coefficients &	coeffs ()
VectorType	intersection (const Hyperplane &other) const
template<typename XprType >
Hyperplane &	transform (const MatrixBase< XprType > &mat, TransformTraits traits=Affine)
template<int TrOptions>
Hyperplane &	transform (const Transform< Scalar, AmbientDimAtCompileTime, Affine, TrOptions > &t, TransformTraits traits=Affine)
template<typename NewScalarType >
internal::cast_return_type < Hyperplane, Hyperplane < NewScalarType, AmbientDimAtCompileTime, Options > >::type	cast () const
template<typename OtherScalarType , int OtherOptions>
	Hyperplane (const Hyperplane< OtherScalarType, AmbientDimAtCompileTime, OtherOptions > &other)
template<int OtherOptions>
bool	isApprox (const Hyperplane< Scalar, AmbientDimAtCompileTime, OtherOptions > &other, const typename NumTraits< Scalar >::Real &prec=NumTraits< Scalar >::dummy_precision()) const
Static Public Member Functions
static Hyperplane	Through (const VectorType &p0, const VectorType &p1)
static Hyperplane	Through (const VectorType &p0, const VectorType &p1, const VectorType &p2)
Protected Attributes
Coefficients	m_coeffs

Detailed Description

template<typename _Scalar, int _AmbientDim, int _Options>
class Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >

A hyperplane.

A hyperplane is an affine subspace of dimension n-1 in a space of dimension n. For example, a hyperplane in a plane is a line; a hyperplane in 3-space is a plane.

Template Parameters:

_Scalar	the scalar type, i.e., the type of the coefficients
_AmbientDim	the dimension of the ambient space, can be a compile time value or Dynamic. Notice that the dimension of the hyperplane is _AmbientDim-1.

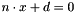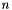This class represents an hyperplane as the zero set of the implicit equation $n \cdot x + d = 0$ where $ n $ is a unit normal vector of the plane (linear part) and 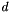$ d $ is the distance (offset) to the origin.

Definition at line 34 of file Hyperplane.h.

Member Typedef Documentation

template<typename _Scalar, int _AmbientDim, int _Options>

typedef Matrix<Scalar,Index(AmbientDimAtCompileTime)==Dynamic ? Dynamic : Index(AmbientDimAtCompileTime)+1,1,Options> Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::Coefficients

Definition at line 48 of file Hyperplane.h.

template<typename _Scalar, int _AmbientDim, int _Options>

typedef const Block<const Coefficients,AmbientDimAtCompileTime,1> Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::ConstNormalReturnType

Definition at line 50 of file Hyperplane.h.

template<typename _Scalar, int _AmbientDim, int _Options>

typedef Eigen::Index Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::Index

Deprecated:: since Eigen 3.3

Definition at line 44 of file Hyperplane.h.

template<typename _Scalar, int _AmbientDim, int _Options>

typedef Block<Coefficients,AmbientDimAtCompileTime,1> Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::NormalReturnType

Definition at line 49 of file Hyperplane.h.

template<typename _Scalar, int _AmbientDim, int _Options>

typedef NumTraits<Scalar>::Real Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::RealScalar

Definition at line 43 of file Hyperplane.h.

template<typename _Scalar, int _AmbientDim, int _Options>

typedef _Scalar Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::Scalar

Definition at line 42 of file Hyperplane.h.

template<typename _Scalar, int _AmbientDim, int _Options>

typedef Matrix<Scalar,AmbientDimAtCompileTime,1> Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::VectorType

Definition at line 45 of file Hyperplane.h.

Member Enumeration Documentation

template<typename _Scalar, int _AmbientDim, int _Options>

anonymous enum

Enumerator:

AmbientDimAtCompileTime
Options

Definition at line 38 of file Hyperplane.h.

       {
    AmbientDimAtCompileTime = _AmbientDim,
    Options = _Options
  };

Constructor & Destructor Documentation

template<typename _Scalar, int _AmbientDim, int _Options>

Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::Hyperplane ( ) [inline]

Default constructor without initialization

Definition at line 53 of file Hyperplane.h.

{}

template<typename _Scalar, int _AmbientDim, int _Options>

template<int OtherOptions>

Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::Hyperplane ( const Hyperplane< Scalar, AmbientDimAtCompileTime, OtherOptions > & other ) [inline]

Definition at line 56 of file Hyperplane.h.

   : m_coeffs(other.coeffs())
  {}

template<typename _Scalar, int _AmbientDim, int _Options>

Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::Hyperplane ( Index _dim ) [inline, explicit]

Constructs a dynamic-size hyperplane with _dim the dimension of the ambient space

Definition at line 62 of file Hyperplane.h.

: m_coeffs(_dim+1) {}

template<typename _Scalar, int _AmbientDim, int _Options>

Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::Hyperplane	(	const VectorType &	n,
		const VectorType &	e
	)		`[inline]`

Construct a plane from its normal n and a point e onto the plane.

Warning:: the vector normal is assumed to be normalized.

Definition at line 67 of file Hyperplane.h.

    : m_coeffs(n.size()+1)
  {
    normal() = n;
    offset() = -n.dot(e);
  }

template<typename _Scalar, int _AmbientDim, int _Options>

Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::Hyperplane	(	const VectorType &	n,
		const Scalar &	d
	)		`[inline]`

Constructs a plane from its normal n and distance to the origin d such that the algebraic equation of the plane is 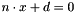$n \cdot x + d = 0$ .

Warning:: the vector normal is assumed to be normalized.

Definition at line 78 of file Hyperplane.h.

    : m_coeffs(n.size()+1)
  {
    normal() = n;
    offset() = d;
  }

template<typename _Scalar, int _AmbientDim, int _Options>

Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::Hyperplane ( const ParametrizedLine< Scalar, AmbientDimAtCompileTime > & parametrized ) [inline, explicit]

Constructs a hyperplane passing through the parametrized line parametrized. If the dimension of the ambient space is greater than 2, then there isn't uniqueness, so an arbitrary choice is made.

Definition at line 123 of file Hyperplane.h.

  {
    normal() = parametrized.direction().unitOrthogonal();
    offset() = -parametrized.origin().dot(normal());
  }

template<typename _Scalar, int _AmbientDim, int _Options>

Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::~Hyperplane ( ) [inline]

Definition at line 129 of file Hyperplane.h.

{}

template<typename _Scalar, int _AmbientDim, int _Options>

template<typename OtherScalarType , int OtherOptions>

Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::Hyperplane ( const Hyperplane< OtherScalarType, AmbientDimAtCompileTime, OtherOptions > & other ) [inline, explicit]

Copy constructor with scalar type conversion

Definition at line 262 of file Hyperplane.h.

  { m_coeffs = other.coeffs().template cast<Scalar>(); }

Member Function Documentation

template<typename _Scalar, int _AmbientDim, int _Options>

Scalar Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::absDistance ( const VectorType & p ) const [inline]

Returns:: the absolute distance between the plane *this and a point p.

See also:: signedDistance()

Definition at line 148 of file Hyperplane.h.

{ using std::abs; return abs(signedDistance(p)); }

template<typename _Scalar, int _AmbientDim, int _Options>

template<typename NewScalarType >

internal::cast_return_type<Hyperplane, Hyperplane<NewScalarType,AmbientDimAtCompileTime,Options> >::type Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::cast ( ) const [inline]

Returns:: *this with scalar type casted to NewScalarType

Note that if NewScalarType is equal to the current scalar type of *this then this function smartly returns a const reference to *this.

Definition at line 254 of file Hyperplane.h.

  {
    return typename internal::cast_return_type<Hyperplane,
                    Hyperplane<NewScalarType,AmbientDimAtCompileTime,Options> >::type(*this);
  }

template<typename _Scalar, int _AmbientDim, int _Options>

const Coefficients& Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::coeffs ( ) const [inline]

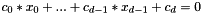
Returns:: a constant reference to the coefficients c_i of the plane equation: $c_0*x_0 + ... + c_{d-1}*x_{d-1} + c_d = 0$

Definition at line 176 of file Hyperplane.h.

{ return m_coeffs; }

template<typename _Scalar, int _AmbientDim, int _Options>

Coefficients& Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::coeffs ( ) [inline]

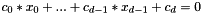
Returns:: a non-constant reference to the coefficients c_i of the plane equation: $c_0*x_0 + ... + c_{d-1}*x_{d-1} + c_d = 0$

Definition at line 181 of file Hyperplane.h.

{ return m_coeffs; }

template<typename _Scalar, int _AmbientDim, int _Options>

Index Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::dim ( ) const [inline]

Returns:: the dimension in which the plane holds

Definition at line 132 of file Hyperplane.h.

{ return AmbientDimAtCompileTime==Dynamic ? m_coeffs.size()-1 : Index(AmbientDimAtCompileTime); }

template<typename _Scalar, int _AmbientDim, int _Options>

VectorType Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::intersection ( const Hyperplane< _Scalar, _AmbientDim, _Options > & other ) const [inline]

Returns:: the intersection of *this with other.

Warning:: The ambient space must be a plane, i.e. have dimension 2, so that *this and other are lines.

Note:: If other is approximately parallel to *this, this method will return any point on *this.

Definition at line 189 of file Hyperplane.h.

  {
    using std::abs;
    EIGEN_STATIC_ASSERT_VECTOR_SPECIFIC_SIZE(VectorType, 2)
    Scalar det = coeffs().coeff(0) * other.coeffs().coeff(1) - coeffs().coeff(1) * other.coeffs().coeff(0);
    // since the line equations ax+by=c are normalized with a^2+b^2=1, the following tests
    // whether the two lines are approximately parallel.
    if(internal::isMuchSmallerThan(det, Scalar(1)))
    {   // special case where the two lines are approximately parallel. Pick any point on the first line.
        if(abs(coeffs().coeff(1))>abs(coeffs().coeff(0)))
            return VectorType(coeffs().coeff(1), -coeffs().coeff(2)/coeffs().coeff(1)-coeffs().coeff(0));
        else
            return VectorType(-coeffs().coeff(2)/coeffs().coeff(0)-coeffs().coeff(1), coeffs().coeff(0));
    }
    else
    {   // general case
        Scalar invdet = Scalar(1) / det;
        return VectorType(invdet*(coeffs().coeff(1)*other.coeffs().coeff(2)-other.coeffs().coeff(1)*coeffs().coeff(2)),
                          invdet*(other.coeffs().coeff(0)*coeffs().coeff(2)-coeffs().coeff(0)*other.coeffs().coeff(2)));
    }
  }

template<typename _Scalar, int _AmbientDim, int _Options>

template<int OtherOptions>

bool Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::isApprox	(	const Hyperplane< Scalar, AmbientDimAtCompileTime, OtherOptions > &	other,
		const typename NumTraits< Scalar >::Real &	prec = `NumTraits<Scalar>::dummy_precision()`
	)		const `[inline]`

Returns:: true if *this is approximately equal to other, within the precision determined by prec.

See also:: MatrixBase::isApprox()

Definition at line 270 of file Hyperplane.h.

  { return m_coeffs.isApprox(other.m_coeffs, prec); }

template<typename _Scalar, int _AmbientDim, int _Options>

ConstNormalReturnType Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::normal ( ) const [inline]

Returns:: a constant reference to the unit normal vector of the plane, which corresponds to the linear part of the implicit equation.

Definition at line 157 of file Hyperplane.h.

{ return ConstNormalReturnType(m_coeffs,0,0,dim(),1); }

template<typename _Scalar, int _AmbientDim, int _Options>

NormalReturnType Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::normal ( ) [inline]

Returns:: a non-constant reference to the unit normal vector of the plane, which corresponds to the linear part of the implicit equation.

Definition at line 162 of file Hyperplane.h.

{ return NormalReturnType(m_coeffs,0,0,dim(),1); }

template<typename _Scalar, int _AmbientDim, int _Options>

void Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::normalize ( void ) [inline]

normalizes *this

Definition at line 135 of file Hyperplane.h.

  {
    m_coeffs /= normal().norm();
  }

template<typename _Scalar, int _AmbientDim, int _Options>

const Scalar& Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::offset ( ) const [inline]

Returns:: the distance to the origin, which is also the "constant term" of the implicit equation

Warning:: the vector normal is assumed to be normalized.

Definition at line 167 of file Hyperplane.h.

{ return m_coeffs.coeff(dim()); }

template<typename _Scalar, int _AmbientDim, int _Options>

Scalar& Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::offset ( ) [inline]

Returns:: a non-constant reference to the distance to the origin, which is also the constant part of the implicit equation

Definition at line 171 of file Hyperplane.h.

{ return m_coeffs(dim()); }

template<typename _Scalar, int _AmbientDim, int _Options>

VectorType Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::projection ( const VectorType & p ) const [inline]

Returns:: the projection of a point p onto the plane *this.

Definition at line 152 of file Hyperplane.h.

{ return p - signedDistance(p) * normal(); }

template<typename _Scalar, int _AmbientDim, int _Options>

Scalar Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::signedDistance ( const VectorType & p ) const [inline]

Returns:: the signed distance between the plane *this and a point p.

See also:: absDistance()

Definition at line 143 of file Hyperplane.h.

{ return normal().dot(p) + offset(); }

template<typename _Scalar, int _AmbientDim, int _Options>

static Hyperplane Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::Through	(	const VectorType &	p0,
		const VectorType &	p1
	)		`[inline, static]`

Constructs a hyperplane passing through the two points. If the dimension of the ambient space is greater than 2, then there isn't uniqueness, so an arbitrary choice is made.

Definition at line 88 of file Hyperplane.h.

  {
    Hyperplane result(p0.size());
    result.normal() = (p1 - p0).unitOrthogonal();
    result.offset() = -p0.dot(result.normal());
    return result;
  }

template<typename _Scalar, int _AmbientDim, int _Options>

static Hyperplane Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::Through	(	const VectorType &	p0,
		const VectorType &	p1,
		const VectorType &	p2
	)		`[inline, static]`

Constructs a hyperplane passing through the three points. The dimension of the ambient space is required to be exactly 3.

Definition at line 99 of file Hyperplane.h.

  {
    EIGEN_STATIC_ASSERT_VECTOR_SPECIFIC_SIZE(VectorType, 3)
    Hyperplane result(p0.size());
    VectorType v0(p2 - p0), v1(p1 - p0);
    result.normal() = v0.cross(v1);
    RealScalar norm = result.normal().norm();
    if(norm <= v0.norm() * v1.norm() * NumTraits<RealScalar>::epsilon())
    {
      Matrix<Scalar,2,3> m; m << v0.transpose(), v1.transpose();
      JacobiSVD<Matrix<Scalar,2,3> > svd(m, ComputeFullV);
      result.normal() = svd.matrixV().col(2);
    }
    else
      result.normal() /= norm;
    result.offset() = -p0.dot(result.normal());
    return result;
  }

template<typename _Scalar, int _AmbientDim, int _Options>

template<typename XprType >

Hyperplane& Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::transform	(	const MatrixBase< XprType > &	mat,
		TransformTraits	traits = `Affine`
	)		`[inline]`

Applies the transformation matrix mat to *this and returns a reference to *this.

Parameters:

mat	the Dim x Dim transformation matrix
traits	specifies whether the matrix mat represents an Isometry or a more generic Affine transformation. The default is Affine.

Definition at line 218 of file Hyperplane.h.

  {
    if (traits==Affine)
      normal() = mat.inverse().transpose() * normal();
    else if (traits==Isometry)
      normal() = mat * normal();
    else
    {
      eigen_assert(0 && "invalid traits value in Hyperplane::transform()");
    }
    return *this;
  }

template<typename _Scalar, int _AmbientDim, int _Options>

template<int TrOptions>

Hyperplane& Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::transform	(	const Transform< Scalar, AmbientDimAtCompileTime, Affine, TrOptions > &	t,
		TransformTraits	traits = `Affine`
	)		`[inline]`

Applies the transformation t to *this and returns a reference to *this.

Parameters:

t	the transformation of dimension Dim
traits	specifies whether the transformation t represents an Isometry or a more generic Affine transformation. The default is Affine. Other kind of transformations are not supported.

Definition at line 239 of file Hyperplane.h.

  {
    transform(t.linear(), traits);
    offset() -= normal().dot(t.translation());
    return *this;
  }

Member Data Documentation

template<typename _Scalar, int _AmbientDim, int _Options>

Coefficients Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >::m_coeffs [protected]

Definition at line 275 of file Hyperplane.h.

The documentation for this class was generated from the following file:

Hyperplane.h

Public Types

Public Member Functions

Static Public Member Functions

Protected Attributes

Detailed Description

template<typename _Scalar, int _AmbientDim, int _Options> class Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >

Member Typedef Documentation

Member Enumeration Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<typename _Scalar, int _AmbientDim, int _Options>
class Eigen::Hyperplane< _Scalar, _AmbientDim, _Options >