MOAB  4.9.3pre
Public Types | Public Member Functions | Static Public Member Functions | Static Protected Member Functions | Protected Attributes | Friends
Eigen::Transform< _Scalar, _Dim, _Mode, _Options > Class Template Reference
Geometry_Module

Represents an homogeneous transformation in a N dimensional space. More...

#include <Transform.h>

Collaboration diagram for Eigen::Transform< _Scalar, _Dim, _Mode, _Options >:
Collaboration graph
[legend]

List of all members.

Public Types

enum  { TransformTimeDiagonalMode = ((Mode==int(Isometry))?Affine:int(Mode)) }
typedef _Scalar Scalar
typedef Eigen::Index StorageIndex
typedef Eigen::Index Index
typedef
internal::make_proper_matrix_type
< Scalar, Rows, HDim, Options >
::type 		MatrixType
typedef const MatrixType ConstMatrixType
typedef Matrix< Scalar, Dim,
Dim, Options > 		LinearMatrixType
typedef Block< MatrixType, Dim,
Dim, int(Mode)==(AffineCompact)&&(Options
&RowMajor)==0 > 		LinearPart
typedef const Block
< ConstMatrixType, Dim, Dim,
int(Mode)==(AffineCompact)&&(Options
&RowMajor)==0 > 		ConstLinearPart
typedef internal::conditional
< int(Mode)==int(AffineCompact),
MatrixType &, Block
< MatrixType, Dim, HDim >
>::type 		AffinePart
typedef internal::conditional
< int(Mode)==int(AffineCompact),
const MatrixType &, const
Block< const MatrixType, Dim,
HDim > >::type 		ConstAffinePart
typedef Matrix< Scalar, Dim, 1 > VectorType
typedef Block< MatrixType, Dim,
1,!(internal::traits
< MatrixType >::Flags
&RowMajorBit)> 		TranslationPart
typedef const Block
< ConstMatrixType, Dim,
1,!(internal::traits
< MatrixType >::Flags
&RowMajorBit)> 		ConstTranslationPart
typedef Translation< Scalar, Dim > TranslationType
typedef Transform< Scalar, Dim,
TransformTimeDiagonalMode > 		TransformTimeDiagonalReturnType
typedef
internal::transform_take_affine_part
< Transform > 		take_affine_part

Public Member Functions

 EIGEN_MAKE_ALIGNED_OPERATOR_NEW_IF_VECTORIZABLE_FIXED_SIZE (_Scalar, _Dim==Dynamic?Dynamic:(_Dim+1)*(_Dim+1)) enum
 Transform ()
 Transform (const Transform &other)
 Transform (const TranslationType &t)
 Transform (const UniformScaling< Scalar > &s)
template<typename Derived >
 Transform (const RotationBase< Derived, Dim > &r)
Transform & operator= (const Transform &other)
template<typename OtherDerived >
 Transform (const EigenBase< OtherDerived > &other)
template<typename OtherDerived >
Transform & operator= (const EigenBase< OtherDerived > &other)
template<int OtherOptions>
 Transform (const Transform< Scalar, Dim, Mode, OtherOptions > &other)
template<int OtherMode, int OtherOptions>
 Transform (const Transform< Scalar, Dim, OtherMode, OtherOptions > &other)
template<typename OtherDerived >
 Transform (const ReturnByValue< OtherDerived > &other)
template<typename OtherDerived >
Transform & operator= (const ReturnByValue< OtherDerived > &other)
Index rows () const
Index cols () const
Scalar operator() (Index row, Index col) const
Scalar & operator() (Index row, Index col)
const MatrixType & matrix () const
MatrixType & matrix ()
ConstLinearPart linear () const
LinearPart linear ()
ConstAffinePart affine () const
AffinePart affine ()
ConstTranslationPart translation () const
TranslationPart translation ()
template<typename OtherDerived >
EIGEN_STRONG_INLINE const
OtherDerived::PlainObject 		operator* (const EigenBase< OtherDerived > &other) const
template<typename DiagonalDerived >
const
TransformTimeDiagonalReturnType 		operator* (const DiagonalBase< DiagonalDerived > &b) const
template<typename OtherDerived >
Transform & operator*= (const EigenBase< OtherDerived > &other)
const Transform operator* (const Transform &other) const
template<int OtherMode, int OtherOptions>
internal::transform_transform_product_impl
< Transform, Transform< Scalar,
Dim, OtherMode, OtherOptions >
>::ResultType 		operator* (const Transform< Scalar, Dim, OtherMode, OtherOptions > &other) const
void setIdentity ()
template<typename OtherDerived >
Transform & scale (const MatrixBase< OtherDerived > &other)
template<typename OtherDerived >
Transform & prescale (const MatrixBase< OtherDerived > &other)
Transform & scale (const Scalar &s)
Transform & prescale (const Scalar &s)
template<typename OtherDerived >
Transform & translate (const MatrixBase< OtherDerived > &other)
template<typename OtherDerived >
Transform & pretranslate (const MatrixBase< OtherDerived > &other)
template<typename RotationType >
Transform & rotate (const RotationType &rotation)
template<typename RotationType >
Transform & prerotate (const RotationType &rotation)
Transform & shear (const Scalar &sx, const Scalar &sy)
Transform & preshear (const Scalar &sx, const Scalar &sy)
Transform & operator= (const TranslationType &t)
Transform & operator*= (const TranslationType &t)
Transform operator* (const TranslationType &t) const
Transform & operator= (const UniformScaling< Scalar > &t)
Transform & operator*= (const UniformScaling< Scalar > &s)
TransformTimeDiagonalReturnType operator* (const UniformScaling< Scalar > &s) const
Transform & operator*= (const DiagonalMatrix< Scalar, Dim > &s)
template<typename Derived >
Transform & operator= (const RotationBase< Derived, Dim > &r)
template<typename Derived >
Transform & operator*= (const RotationBase< Derived, Dim > &r)
template<typename Derived >
Transform operator* (const RotationBase< Derived, Dim > &r) const
const LinearMatrixType rotation () const
template<typename RotationMatrixType , typename ScalingMatrixType >
void computeRotationScaling (RotationMatrixType *rotation, ScalingMatrixType *scaling) const
template<typename ScalingMatrixType , typename RotationMatrixType >
void computeScalingRotation (ScalingMatrixType *scaling, RotationMatrixType *rotation) const
template<typename PositionDerived , typename OrientationType , typename ScaleDerived >
Transform & fromPositionOrientationScale (const MatrixBase< PositionDerived > &position, const OrientationType &orientation, const MatrixBase< ScaleDerived > &scale)
Transform inverse (TransformTraits traits=(TransformTraits) Mode) const
const Scalar * data () const
Scalar * data ()
template<typename NewScalarType >
internal::cast_return_type
< Transform, Transform
< NewScalarType, Dim, Mode,
Options > >::type 		cast () const
template<typename OtherScalarType >
 Transform (const Transform< OtherScalarType, Dim, Mode, Options > &other)
bool isApprox (const Transform &other, const typename NumTraits< Scalar >::Real &prec=NumTraits< Scalar >::dummy_precision()) const
void makeAffine ()
Block< MatrixType, int(Mode)==int(Projective)?HDim:Dim,
Dim > 		linearExt ()
const Block< MatrixType, int(Mode)==int(Projective)?HDim:Dim,
Dim > 		linearExt () const
Block< MatrixType, int(Mode)==int(Projective)?HDim:Dim, 1 > translationExt ()
const Block< MatrixType, int(Mode)==int(Projective)?HDim:Dim, 1 > translationExt () const

Static Public Member Functions

static const Transform Identity ()
 Returns an identity transformation.

Static Protected Member Functions

static EIGEN_STRONG_INLINE void check_template_params ()

Protected Attributes

MatrixType m_matrix

Friends

template<typename OtherDerived >
const
internal::transform_left_product_impl
< OtherDerived, Mode, Options,
_Dim, _Dim+1 >::ResultType 		operator* (const EigenBase< OtherDerived > &a, const Transform &b)
template<typename DiagonalDerived >
TransformTimeDiagonalReturnType operator* (const DiagonalBase< DiagonalDerived > &a, const Transform &b)

Detailed Description

template<typename _Scalar, int _Dim, int _Mode, int _Options>
class Eigen::Transform< _Scalar, _Dim, _Mode, _Options >

Represents an homogeneous transformation in a N dimensional space.

Template Parameters:
_Scalarthe scalar type, i.e., the type of the coefficients
_Dimthe dimension of the space
_Modethe type of the transformation. Can be:
  • Affine: the transformation is stored as a (Dim+1)^2 matrix, where the last row is assumed to be [0 ... 0 1].
  • AffineCompact: the transformation is stored as a (Dim)x(Dim+1) matrix.
  • Projective: the transformation is stored as a (Dim+1)^2 matrix without any assumption.
_Optionshas the same meaning as in class Matrix. It allows to specify DontAlign and/or RowMajor. These Options are passed directly to the underlying matrix type.

The homography is internally represented and stored by a matrix which is available through the matrix() method. To understand the behavior of this class you have to think a Transform object as its internal matrix representation. The chosen convention is right multiply:

 v' = T * v

Therefore, an affine transformation matrix M is shaped like this:

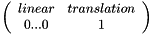
$ \left( \begin{array}{cc} linear & translation\\ 0 ... 0 & 1 \end{array} \right) $

Note that for a projective transformation the last row can be anything, and then the interpretation of different parts might be sightly different.

However, unlike a plain matrix, the Transform class provides many features simplifying both its assembly and usage. In particular, it can be composed with any other transformations (Transform,Translation,RotationBase,DiagonalMatrix) and can be directly used to transform implicit homogeneous vectors. All these operations are handled via the operator*. For the composition of transformations, its principle consists to first convert the right/left hand sides of the product to a compatible (Dim+1)^2 matrix and then perform a pure matrix product. Of course, internally, operator* tries to perform the minimal number of operations according to the nature of each terms. Likewise, when applying the transform to points, the latters are automatically promoted to homogeneous vectors before doing the matrix product. The conventions to homogeneous representations are performed as follow:

Translation t (Dim)x(1): 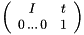$ \left( \begin{array}{cc} I & t \\ 0\,...\,0 & 1 \end{array} \right) $

Rotation R (Dim)x(Dim): 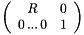$ \left( \begin{array}{cc} R & 0\\ 0\,...\,0 & 1 \end{array} \right) $

Scaling DiagonalMatrix S (Dim)x(Dim): 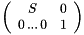$ \left( \begin{array}{cc} S & 0\\ 0\,...\,0 & 1 \end{array} \right) $

Column point v (Dim)x(1): 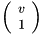$ \left( \begin{array}{c} v\\ 1 \end{array} \right) $

Set of column points V1...Vn (Dim)x(n): $ \left( \begin{array}{ccc} v_1 & ... & v_n\\ 1 & ... & 1 \end{array} \right) $

The concatenation of a Transform object with any kind of other transformation always returns a Transform object.

A little exception to the "as pure matrix product" rule is the case of the transformation of non homogeneous vectors by an affine transformation. In that case the last matrix row can be ignored, and the product returns non homogeneous vectors.

Since, for instance, a Dim x Dim matrix is interpreted as a linear transformation, it is not possible to directly transform Dim vectors stored in a Dim x Dim matrix. The solution is either to use a Dim x Dynamic matrix or explicitly request a vector transformation by making the vector homogeneous: 

 m' = T * m.colwise().homogeneous();

Note that there is zero overhead.

Conversion methods from/to Qt's QMatrix and QTransform are available if the preprocessor token EIGEN_QT_SUPPORT is defined.

This class can be extended with the help of the plugin mechanism described on the page TopicCustomizingEigen by defining the preprocessor symbol EIGEN_TRANSFORM_PLUGIN.

See also:
class Matrix, class Quaternion

Definition at line 200 of file Transform.h.

Member Typedef Documentation

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef internal::conditional<int(Mode)==int(AffineCompact), MatrixType&, Block<MatrixType,Dim,HDim> >::type Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::AffinePart

type of read/write reference to the affine part of the transformation

Definition at line 228 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef internal::conditional<int(Mode)==int(AffineCompact), const MatrixType&, const Block<const MatrixType,Dim,HDim> >::type Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::ConstAffinePart

type of read reference to the affine part of the transformation

Definition at line 232 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef const Block<ConstMatrixType,Dim,Dim,int(Mode)==(AffineCompact) && (Options&RowMajor)==0> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::ConstLinearPart

type of read reference to the linear part of the transformation

Definition at line 224 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef const MatrixType Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::ConstMatrixType

constified MatrixType

Definition at line 218 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef const Block<ConstMatrixType,Dim,1,!(internal::traits<MatrixType>::Flags & RowMajorBit)> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::ConstTranslationPart

type of a read reference to the translation part of the rotation

Definition at line 238 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef Eigen::Index Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Index
Deprecated:
since Eigen 3.3

Definition at line 214 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef Matrix<Scalar,Dim,Dim,Options> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::LinearMatrixType

type of the matrix used to represent the linear part of the transformation

Definition at line 220 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef Block<MatrixType,Dim,Dim,int(Mode)==(AffineCompact) && (Options&RowMajor)==0> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::LinearPart

type of read/write reference to the linear part of the transformation

Definition at line 222 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef internal::make_proper_matrix_type<Scalar,Rows,HDim,Options>::type Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::MatrixType

type of the matrix used to represent the transformation

Definition at line 216 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef _Scalar Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Scalar

the scalar type of the coefficients

Definition at line 210 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef Eigen::Index Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::StorageIndex

Definition at line 213 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef internal::transform_take_affine_part<Transform> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::take_affine_part

Definition at line 287 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef Transform<Scalar,Dim,TransformTimeDiagonalMode> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::TransformTimeDiagonalReturnType

The return type of the product between a diagonal matrix and a transform

Definition at line 245 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef Block<MatrixType,Dim,1,!(internal::traits<MatrixType>::Flags & RowMajorBit)> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::TranslationPart

type of a read/write reference to the translation part of the rotation

Definition at line 236 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef Translation<Scalar,Dim> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::TranslationType

corresponding translation type

Definition at line 240 of file Transform.h.

template<typename _Scalar, int _Dim, int _Mode, int _Options>
typedef Matrix<Scalar,Dim,1> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::VectorType

type of a vector

Definition at line 234 of file Transform.h.

Member Enumeration Documentation

template<typename _Scalar, int _Dim, int _Mode, int _Options>
anonymous enum
Enumerator:
TransformTimeDiagonalMode 

Definition at line 243 of file Transform.h.

{ TransformTimeDiagonalMode = ((Mode==int(Isometry))?Affine:int(Mode)) };

Constructor & Destructor Documentation

template<typename _Scalar, int _Dim, int _Mode, int _Options>
Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Transform ( ) [inline]

Default constructor without initialization of the meaningful coefficients. If Mode==Affine, then the last row is set to [0 ... 0 1]

Definition at line 255 of file Transform.h.

  {
    check_template_params();
    internal::transform_make_affine<(int(Mode)==Affine) ? Affine : AffineCompact>::run(m_matrix);
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Transform ( const Transform< _Scalar, _Dim, _Mode, _Options > &  other) [inline]

Definition at line 261 of file Transform.h.

  {
    check_template_params();
    m_matrix = other.m_matrix;
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Transform ( const TranslationType &  t) [inline, explicit]

Definition at line 267 of file Transform.h.

  {
    check_template_params();
    *this = t;
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Transform ( const UniformScaling< Scalar > &  s) [inline, explicit]

Definition at line 272 of file Transform.h.

  {
    check_template_params();
    *this = s;
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename Derived >
Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Transform ( const RotationBase< Derived, Dim > &  r) [inline, explicit]

Definition at line 278 of file Transform.h.

  {
    check_template_params();
    *this = r;
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename OtherDerived >
Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Transform ( const EigenBase< OtherDerived > &  other) [inline, explicit]

Constructs and initializes a transformation from a Dim^2 or a (Dim+1)^2 matrix.

Definition at line 291 of file Transform.h.

  {
    EIGEN_STATIC_ASSERT((internal::is_same<Scalar,typename OtherDerived::Scalar>::value),
      YOU_MIXED_DIFFERENT_NUMERIC_TYPES__YOU_NEED_TO_USE_THE_CAST_METHOD_OF_MATRIXBASE_TO_CAST_NUMERIC_TYPES_EXPLICITLY);

    check_template_params();
    internal::transform_construct_from_matrix<OtherDerived,Mode,Options,Dim,HDim>::run(this, other.derived());
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<int OtherOptions>
Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Transform ( const Transform< Scalar, Dim, Mode, OtherOptions > &  other) [inline]

Definition at line 312 of file Transform.h.

  {
    check_template_params();
    // only the options change, we can directly copy the matrices
    m_matrix = other.matrix();
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<int OtherMode, int OtherOptions>
Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Transform ( const Transform< Scalar, Dim, OtherMode, OtherOptions > &  other) [inline]

Definition at line 320 of file Transform.h.

  {
    check_template_params();
    // prevent conversions as:
    // Affine | AffineCompact | Isometry = Projective
    EIGEN_STATIC_ASSERT(EIGEN_IMPLIES(OtherMode==int(Projective), Mode==int(Projective)),
                        YOU_PERFORMED_AN_INVALID_TRANSFORMATION_CONVERSION)

    // prevent conversions as:
    // Isometry = Affine | AffineCompact
    EIGEN_STATIC_ASSERT(EIGEN_IMPLIES(OtherMode==int(Affine)||OtherMode==int(AffineCompact), Mode!=int(Isometry)),
                        YOU_PERFORMED_AN_INVALID_TRANSFORMATION_CONVERSION)

    enum { ModeIsAffineCompact = Mode == int(AffineCompact),
           OtherModeIsAffineCompact = OtherMode == int(AffineCompact)
    };

    if(ModeIsAffineCompact == OtherModeIsAffineCompact)
    {
      // We need the block expression because the code is compiled for all
      // combinations of transformations and will trigger a compile time error
      // if one tries to assign the matrices directly
      m_matrix.template block<Dim,Dim+1>(0,0) = other.matrix().template block<Dim,Dim+1>(0,0);
      makeAffine();
    }
    else if(OtherModeIsAffineCompact)
    {
      typedef typename Transform<Scalar,Dim,OtherMode,OtherOptions>::MatrixType OtherMatrixType;
      internal::transform_construct_from_matrix<OtherMatrixType,Mode,Options,Dim,HDim>::run(this, other.matrix());
    }
    else
    {
      // here we know that Mode == AffineCompact and OtherMode != AffineCompact.
      // if OtherMode were Projective, the static assert above would already have caught it.
      // So the only possibility is that OtherMode == Affine
      linear() = other.linear();
      translation() = other.translation();
    }
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename OtherDerived >
Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Transform ( const ReturnByValue< OtherDerived > &  other) [inline]

Definition at line 361 of file Transform.h.

  {
    check_template_params();
    other.evalTo(*this);
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename OtherScalarType >
Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Transform ( const Transform< OtherScalarType, Dim, Mode, Options > &  other) [inline, explicit]

Copy constructor with scalar type conversion

Definition at line 617 of file Transform.h.

  {
    check_template_params();
    m_matrix = other.matrix().template cast<Scalar>();
  }

Member Function Documentation

template<typename _Scalar, int _Dim, int _Mode, int _Options>
ConstAffinePart Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::affine ( ) const [inline]
Returns:
a read-only expression of the Dim x HDim affine part of the transformation

Definition at line 404 of file Transform.h.

{ return take_affine_part::run(m_matrix); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
AffinePart Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::affine ( ) [inline]
Returns:
a writable expression of the Dim x HDim affine part of the transformation

Definition at line 406 of file Transform.h.

{ return take_affine_part::run(m_matrix); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename NewScalarType >
internal::cast_return_type<Transform,Transform<NewScalarType,Dim,Mode,Options> >::type Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::cast ( ) const [inline]
Returns:
*this with scalar type casted to NewScalarType

Note that if NewScalarType is equal to the current scalar type of *this then this function smartly returns a const reference to *this.

Definition at line 612 of file Transform.h.

  { return typename internal::cast_return_type<Transform,Transform<NewScalarType,Dim,Mode,Options> >::type(*this); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
static EIGEN_STRONG_INLINE void Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::check_template_params ( ) [inline, static, protected]

Definition at line 670 of file Transform.h.

    {
      EIGEN_STATIC_ASSERT((Options & (DontAlign|RowMajor)) == Options, INVALID_MATRIX_TEMPLATE_PARAMETERS)
    }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Index Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::cols ( void  ) const [inline]

Definition at line 384 of file Transform.h.

{ return m_matrix.cols(); }
template<typename Scalar , int Dim, int Mode, int Options>
template<typename RotationMatrixType , typename ScalingMatrixType >
void Eigen::Transform< Scalar, Dim, Mode, Options >::computeRotationScaling ( RotationMatrixType *  rotation,
ScalingMatrixType *  scaling 
) const

decomposes the linear part of the transformation as a product rotation x scaling, the scaling being not necessarily positive.

If either pointer is zero, the corresponding computation is skipped.

See also:
computeScalingRotation(), rotation(), class SVD

Definition at line 1059 of file Transform.h.

{
  JacobiSVD<LinearMatrixType> svd(linear(), ComputeFullU | ComputeFullV);

  Scalar x = (svd.matrixU() * svd.matrixV().adjoint()).determinant(); // so x has absolute value 1
  VectorType sv(svd.singularValues());
  sv.coeffRef(0) *= x;
  if(scaling) scaling->lazyAssign(svd.matrixV() * sv.asDiagonal() * svd.matrixV().adjoint());
  if(rotation)
  {
    LinearMatrixType m(svd.matrixU());
    m.col(0) /= x;
    rotation->lazyAssign(m * svd.matrixV().adjoint());
  }
}
template<typename Scalar , int Dim, int Mode, int Options>
template<typename ScalingMatrixType , typename RotationMatrixType >
void Eigen::Transform< Scalar, Dim, Mode, Options >::computeScalingRotation ( ScalingMatrixType *  scaling,
RotationMatrixType *  rotation 
) const

decomposes the linear part of the transformation as a product rotation x scaling, the scaling being not necessarily positive.

If either pointer is zero, the corresponding computation is skipped.

See also:
computeRotationScaling(), rotation(), class SVD

Definition at line 1088 of file Transform.h.

{
  JacobiSVD<LinearMatrixType> svd(linear(), ComputeFullU | ComputeFullV);

  Scalar x = (svd.matrixU() * svd.matrixV().adjoint()).determinant(); // so x has absolute value 1
  VectorType sv(svd.singularValues());
  sv.coeffRef(0) *= x;
  if(scaling) scaling->lazyAssign(svd.matrixU() * sv.asDiagonal() * svd.matrixU().adjoint());
  if(rotation)
  {
    LinearMatrixType m(svd.matrixU());
    m.col(0) /= x;
    rotation->lazyAssign(m * svd.matrixV().adjoint());
  }
}
template<typename _Scalar, int _Dim, int _Mode, int _Options>
const Scalar* Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::data ( ) const [inline]
Returns:
a const pointer to the column major internal matrix

Definition at line 602 of file Transform.h.

{ return m_matrix.data(); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Scalar* Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::data ( ) [inline]
Returns:
a non-const pointer to the column major internal matrix

Definition at line 604 of file Transform.h.

{ return m_matrix.data(); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::EIGEN_MAKE_ALIGNED_OPERATOR_NEW_IF_VECTORIZABLE_FIXED_SIZE ( _Scalar  ,
_Dim  = =Dynamic ? Dynamic : (_Dim+1)*(_Dim+1) 
) [inline]

< space dimension in which the transformation holds

< size of a respective homogeneous vector

Definition at line 203 of file Transform.h.

                                                                                             : (_Dim+1)*(_Dim+1))
  enum {
    Mode = _Mode,
    Options = _Options,
    Dim = _Dim,     
    HDim = _Dim+1,  
    Rows = int(Mode)==(AffineCompact) ? Dim : HDim
  };
template<typename Scalar , int Dim, int Mode, int Options>
template<typename PositionDerived , typename OrientationType , typename ScaleDerived >
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::fromPositionOrientationScale ( const MatrixBase< PositionDerived > &  position,
const OrientationType &  orientation,
const MatrixBase< ScaleDerived > &  scale 
)

Convenient method to set *this from a position, orientation and scale of a 3D object.

Definition at line 1110 of file Transform.h.

{
  linear() = internal::toRotationMatrix<Scalar,Dim>(orientation);
  linear() *= scale.asDiagonal();
  translation() = position;
  makeAffine();
  return *this;
}
template<typename _Scalar, int _Dim, int _Mode, int _Options>
static const Transform Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::Identity ( ) [inline, static]

Returns an identity transformation.

Todo:
In the future this function should be returning a Transform expression.

Definition at line 538 of file Transform.h.

  {
    return Transform(MatrixType::Identity());
  }
template<typename Scalar , int Dim, int Mode, int Options>
Transform< Scalar, Dim, Mode, Options > Eigen::Transform< Scalar, Dim, Mode, Options >::inverse ( TransformTraits  hint = (TransformTraits)Mode) const [inline]
Returns:
the inverse transformation according to some given knowledge on *this.
Parameters:
hintallows to optimize the inversion process when the transformation is known to be not a general transformation (optional). The possible values are:
  • Projective if the transformation is not necessarily affine, i.e., if the last row is not guaranteed to be [0 ... 0 1]
  • Affine if the last row can be assumed to be [0 ... 0 1]
  • Isometry if the transformation is only a concatenations of translations and rotations. The default is the template class parameter Mode.
Warning:
unless traits is always set to NoShear or NoScaling, this function requires the generic inverse method of MatrixBase defined in the LU module. If you forget to include this module, then you will get hard to debug linking errors.
See also:
MatrixBase::inverse()

Definition at line 1182 of file Transform.h.

{
  Transform res;
  if (hint == Projective)
  {
    internal::projective_transform_inverse<Transform>::run(*this, res);
  }
  else
  {
    if (hint == Isometry)
    {
      res.matrix().template topLeftCorner<Dim,Dim>() = linear().transpose();
    }
    else if(hint&Affine)
    {
      res.matrix().template topLeftCorner<Dim,Dim>() = linear().inverse();
    }
    else
    {
      eigen_assert(false && "Invalid transform traits in Transform::Inverse");
    }
    // translation and remaining parts
    res.matrix().template topRightCorner<Dim,1>()
      = - res.matrix().template topLeftCorner<Dim,Dim>() * translation();
    res.makeAffine(); // we do need this, because in the beginning res is uninitialized
  }
  return res;
}
template<typename _Scalar, int _Dim, int _Mode, int _Options>
bool Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::isApprox ( const Transform< _Scalar, _Dim, _Mode, _Options > &  other,
const typename NumTraits< Scalar >::Real &  prec = NumTraits<Scalar>::dummy_precision() 
) const [inline]
Returns:
true if *this is approximately equal to other, within the precision determined by prec.
See also:
MatrixBase::isApprox()

Definition at line 627 of file Transform.h.

  { return m_matrix.isApprox(other.m_matrix, prec); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
ConstLinearPart Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::linear ( ) const [inline]
Returns:
a read-only expression of the linear part of the transformation

Definition at line 399 of file Transform.h.

{ return ConstLinearPart(m_matrix,0,0); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
LinearPart Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::linear ( ) [inline]
Returns:
a writable expression of the linear part of the transformation

Definition at line 401 of file Transform.h.

{ return LinearPart(m_matrix,0,0); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Block<MatrixType,int(Mode)==int(Projective)?HDim:Dim,Dim> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::linearExt ( ) [inline]
Returns:
the Dim x Dim linear part if the transformation is affine, and the HDim x Dim part for projective transformations.

Definition at line 641 of file Transform.h.

                                                         :Dim,Dim> linearExt()
  { return m_matrix.template block<int(Mode)==int(Projective)?HDim:Dim,Dim>(0,0); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
const Block<MatrixType,int(Mode)==int(Projective)?HDim:Dim,Dim> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::linearExt ( ) const [inline]
Returns:
the Dim x Dim linear part if the transformation is affine, and the HDim x Dim part for projective transformations.

Definition at line 647 of file Transform.h.

                                                               :Dim,Dim> linearExt() const
  { return m_matrix.template block<int(Mode)==int(Projective)?HDim:Dim,Dim>(0,0); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
void Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::makeAffine ( ) [inline]

Sets the last row to [0 ... 0 1]

Definition at line 632 of file Transform.h.

  {
    internal::transform_make_affine<int(Mode)>::run(m_matrix);
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
const MatrixType& Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::matrix ( ) const [inline]
Returns:
a read-only expression of the transformation matrix

Definition at line 394 of file Transform.h.

{ return m_matrix; }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
MatrixType& Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::matrix ( ) [inline]
Returns:
a writable expression of the transformation matrix

Definition at line 396 of file Transform.h.

{ return m_matrix; }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Scalar Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator() ( Index  row,
Index  col 
) const [inline]

shortcut for m_matrix(row,col);

See also:
MatrixBase::operator(Index,Index) const

Definition at line 388 of file Transform.h.

{ return m_matrix(row,col); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Scalar& Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator() ( Index  row,
Index  col 
) [inline]

shortcut for m_matrix(row,col);

See also:
MatrixBase::operator(Index,Index)

Definition at line 391 of file Transform.h.

{ return m_matrix(row,col); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename OtherDerived >
EIGEN_STRONG_INLINE const OtherDerived::PlainObject Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator* ( const EigenBase< OtherDerived > &  other) const [inline]
Returns:
an expression of the product between the transform *this and a matrix expression other.

The right-hand-side other can be either:

  • an homogeneous vector of size Dim+1,
  • a set of homogeneous vectors of size Dim+1 x N,
  • a transformation matrix of size Dim+1 x Dim+1.

Moreover, if *this represents an affine transformation (i.e., Mode!=Projective), then other can also be:

  • a point of size Dim (computes: 
     this->linear() * other + this->translation()
    ),
  • a set of N points as a Dim x N matrix (computes: 
     (this->linear() * other).colwise() + this->translation()
    ),

In all cases, the return type is a matrix or vector of same sizes as the right-hand-side other.

If you want to interpret other as a linear or affine transformation, then first convert it to a Transform<> type, or do your own cooking.

Finally, if you want to apply Affine transformations to vectors, then explicitly apply the linear part only: 

 Affine3f A;
 Vector3f v1, v2;
 v2 = A.linear() * v1;

Definition at line 440 of file Transform.h.

  { return internal::transform_right_product_impl<Transform, OtherDerived>::run(*this,other.derived()); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename DiagonalDerived >
const TransformTimeDiagonalReturnType Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator* ( const DiagonalBase< DiagonalDerived > &  b) const [inline]
Returns:
The product expression of a transform a times a diagonal matrix b

The rhs diagonal matrix is interpreted as an affine scaling transformation. The product results in a Transform of the same type (mode) as the lhs only if the lhs mode is no isometry. In that case, the returned transform is an affinity.

Definition at line 463 of file Transform.h.

  {
    TransformTimeDiagonalReturnType res(*this);
    res.linear() *= b;
    return res;
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
const Transform Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator* ( const Transform< _Scalar, _Dim, _Mode, _Options > &  other) const [inline]

Concatenates two transformations

Definition at line 492 of file Transform.h.

  {
    return internal::transform_transform_product_impl<Transform,Transform>::run(*this,other);
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<int OtherMode, int OtherOptions>
internal::transform_transform_product_impl<Transform,Transform<Scalar,Dim,OtherMode,OtherOptions> >::ResultType Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator* ( const Transform< Scalar, Dim, OtherMode, OtherOptions > &  other) const [inline]

Concatenates two different transformations

Definition at line 525 of file Transform.h.

  {
    return internal::transform_transform_product_impl<Transform,Transform<Scalar,Dim,OtherMode,OtherOptions> >::run(*this,other);
  }
template<typename Scalar , int Dim, int Mode, int Options>
Transform< Scalar, Dim, Mode, Options > Eigen::Transform< Scalar, Dim, Mode, Options >::operator* ( const TranslationType &  t) const [inline]

Definition at line 990 of file Transform.h.

{
  Transform res = *this;
  res.translate(t.vector());
  return res;
}
template<typename _Scalar, int _Dim, int _Mode, int _Options>
TransformTimeDiagonalReturnType Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator* ( const UniformScaling< Scalar > &  s) const [inline]

Definition at line 573 of file Transform.h.

  {
    TransformTimeDiagonalReturnType res = *this;
    res.scale(s.factor());
    return res;
  }
template<typename Scalar , int Dim, int Mode, int Options>
template<typename Derived>
Transform< Scalar, Dim, Mode, Options > Eigen::Transform< Scalar, Dim, Mode, Options >::operator* ( const RotationBase< Derived, Dim > &  r) const [inline]

Definition at line 1018 of file Transform.h.

{
  Transform res = *this;
  res.rotate(r.derived());
  return res;
}
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename OtherDerived >
Transform& Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator*= ( const EigenBase< OtherDerived > &  other) [inline]

Definition at line 489 of file Transform.h.

{ return *this = *this * other; }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Transform& Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator*= ( const TranslationType &  t) [inline]

Definition at line 568 of file Transform.h.

{ return translate(t.vector()); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Transform& Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator*= ( const UniformScaling< Scalar > &  s) [inline]

Definition at line 572 of file Transform.h.

{ return scale(s.factor()); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Transform& Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator*= ( const DiagonalMatrix< Scalar, Dim > &  s) [inline]

Definition at line 580 of file Transform.h.

{ linear() *= s; return *this; }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename Derived >
Transform& Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator*= ( const RotationBase< Derived, Dim > &  r) [inline]

Definition at line 585 of file Transform.h.

{ return rotate(r.toRotationMatrix()); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Transform& Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator= ( const Transform< _Scalar, _Dim, _Mode, _Options > &  other) [inline]

Definition at line 284 of file Transform.h.

  { m_matrix = other.m_matrix; return *this; }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename OtherDerived >
Transform& Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator= ( const EigenBase< OtherDerived > &  other) [inline]

Set *this from a Dim^2 or (Dim+1)^2 matrix.

Definition at line 302 of file Transform.h.

  {
    EIGEN_STATIC_ASSERT((internal::is_same<Scalar,typename OtherDerived::Scalar>::value),
      YOU_MIXED_DIFFERENT_NUMERIC_TYPES__YOU_NEED_TO_USE_THE_CAST_METHOD_OF_MATRIXBASE_TO_CAST_NUMERIC_TYPES_EXPLICITLY);

    internal::transform_construct_from_matrix<OtherDerived,Mode,Options,Dim,HDim>::run(this, other.derived());
    return *this;
  }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename OtherDerived >
Transform& Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::operator= ( const ReturnByValue< OtherDerived > &  other) [inline]

Definition at line 368 of file Transform.h.

  {
    other.evalTo(*this);
    return *this;
  }
template<typename Scalar , int Dim, int Mode, int Options>
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::operator= ( const TranslationType &  t) [inline]

Definition at line 981 of file Transform.h.

{
  linear().setIdentity();
  translation() = t.vector();
  makeAffine();
  return *this;
}
template<typename Scalar , int Dim, int Mode, int Options>
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::operator= ( const UniformScaling< Scalar > &  t) [inline]

Definition at line 998 of file Transform.h.

{
  m_matrix.setZero();
  linear().diagonal().fill(s.factor());
  makeAffine();
  return *this;
}
template<typename Scalar , int Dim, int Mode, int Options>
template<typename Derived >
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::operator= ( const RotationBase< Derived, Dim > &  r) [inline]

Definition at line 1008 of file Transform.h.

{
  linear() = internal::toRotationMatrix<Scalar,Dim>(r);
  translation().setZero();
  makeAffine();
  return *this;
}
template<typename Scalar , int Dim, int Mode, int Options>
template<typename RotationType >
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::prerotate ( const RotationType &  rotation) [inline]

Applies on the left the rotation represented by the rotation rotation to *this and returns a reference to *this.

See rotate() for further details.

See also:
rotate()

Definition at line 938 of file Transform.h.

{
  m_matrix.template block<Dim,HDim>(0,0) = internal::toRotationMatrix<Scalar,Dim>(rotation)
                                         * m_matrix.template block<Dim,HDim>(0,0);
  return *this;
}
template<typename Scalar , int Dim, int Mode, int Options>
template<typename OtherDerived >
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::prescale ( const MatrixBase< OtherDerived > &  other) [inline]

Applies on the left the non uniform scale transformation represented by the vector other to *this and returns a reference to *this.

See also:
scale()

Definition at line 851 of file Transform.h.

{
  EIGEN_STATIC_ASSERT_VECTOR_SPECIFIC_SIZE(OtherDerived,int(Dim))
  EIGEN_STATIC_ASSERT(Mode!=int(Isometry), THIS_METHOD_IS_ONLY_FOR_SPECIFIC_TRANSFORMATIONS)
  m_matrix.template block<Dim,HDim>(0,0).noalias() = (other.asDiagonal() * m_matrix.template block<Dim,HDim>(0,0));
  return *this;
}
template<typename Scalar , int Dim, int Mode, int Options>
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::prescale ( const Scalar &  s) [inline]

Applies on the left a uniform scale of a factor c to *this and returns a reference to *this.

See also:
scale(Scalar)

Definition at line 864 of file Transform.h.

{
  EIGEN_STATIC_ASSERT(Mode!=int(Isometry), THIS_METHOD_IS_ONLY_FOR_SPECIFIC_TRANSFORMATIONS)
  m_matrix.template topRows<Dim>() *= s;
  return *this;
}
template<typename Scalar , int Dim, int Mode, int Options>
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::preshear ( const Scalar &  sx,
const Scalar &  sy 
)

Applies on the left the shear transformation represented by the vector other to *this and returns a reference to *this.

Warning:
2D only.
See also:
shear()

Definition at line 968 of file Transform.h.

{
  EIGEN_STATIC_ASSERT(int(Dim)==2, YOU_MADE_A_PROGRAMMING_MISTAKE)
  EIGEN_STATIC_ASSERT(Mode!=int(Isometry), THIS_METHOD_IS_ONLY_FOR_SPECIFIC_TRANSFORMATIONS)
  m_matrix.template block<Dim,HDim>(0,0) = LinearMatrixType(1, sx, sy, 1) * m_matrix.template block<Dim,HDim>(0,0);
  return *this;
}
template<typename Scalar , int Dim, int Mode, int Options>
template<typename OtherDerived >
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::pretranslate ( const MatrixBase< OtherDerived > &  other) [inline]

Applies on the left the translation matrix represented by the vector other to *this and returns a reference to *this.

See also:
translate()

Definition at line 892 of file Transform.h.

{
  EIGEN_STATIC_ASSERT_VECTOR_SPECIFIC_SIZE(OtherDerived,int(Dim))
  if(int(Mode)==int(Projective))
    affine() += other * m_matrix.row(Dim);
  else
    translation() += other;
  return *this;
}
template<typename Scalar , int Dim, int Mode, int Options>
template<typename RotationType >
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::rotate ( const RotationType &  rotation) [inline]

Applies on the right the rotation represented by the rotation rotation to *this and returns a reference to *this.

The template parameter RotationType is the type of the rotation which must be known by internal::toRotationMatrix<>.

Natively supported types includes:

This mechanism is easily extendable to support user types such as Euler angles, or a pair of Quaternion for 4D rotations.

See also:
rotate(Scalar), class Quaternion, class AngleAxis, prerotate(RotationType)

Definition at line 922 of file Transform.h.

{
  linearExt() *= internal::toRotationMatrix<Scalar,Dim>(rotation);
  return *this;
}
template<typename Scalar , int Dim, int Mode, int Options>
const Transform< Scalar, Dim, Mode, Options >::LinearMatrixType Eigen::Transform< Scalar, Dim, Mode, Options >::rotation ( ) const
Returns:
the rotation part of the transformation
See also:
computeRotationScaling(), computeScalingRotation(), class SVD

Definition at line 1038 of file Transform.h.

{
  LinearMatrixType result;
  computeRotationScaling(&result, (LinearMatrixType*)0);
  return result;
}
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Index Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::rows ( void  ) const [inline]

Definition at line 383 of file Transform.h.

{ return int(Mode)==int(Projective) ? m_matrix.cols() : (m_matrix.cols()-1); }
template<typename Scalar , int Dim, int Mode, int Options>
template<typename OtherDerived >
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::scale ( const MatrixBase< OtherDerived > &  other) [inline]

Applies on the right the non uniform scale transformation represented by the vector other to *this and returns a reference to *this.

See also:
prescale()

Definition at line 824 of file Transform.h.

{
  EIGEN_STATIC_ASSERT_VECTOR_SPECIFIC_SIZE(OtherDerived,int(Dim))
  EIGEN_STATIC_ASSERT(Mode!=int(Isometry), THIS_METHOD_IS_ONLY_FOR_SPECIFIC_TRANSFORMATIONS)
  linearExt().noalias() = (linearExt() * other.asDiagonal());
  return *this;
}
template<typename Scalar , int Dim, int Mode, int Options>
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::scale ( const Scalar &  s) [inline]

Applies on the right a uniform scale of a factor c to *this and returns a reference to *this.

See also:
prescale(Scalar)

Definition at line 837 of file Transform.h.

{
  EIGEN_STATIC_ASSERT(Mode!=int(Isometry), THIS_METHOD_IS_ONLY_FOR_SPECIFIC_TRANSFORMATIONS)
  linearExt() *= s;
  return *this;
}
template<typename _Scalar, int _Dim, int _Mode, int _Options>
void Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::setIdentity ( ) [inline]
See also:
MatrixBase::setIdentity()

Definition at line 532 of file Transform.h.

{ m_matrix.setIdentity(); }
template<typename Scalar , int Dim, int Mode, int Options>
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::shear ( const Scalar &  sx,
const Scalar &  sy 
)

Applies on the right the shear transformation represented by the vector other to *this and returns a reference to *this.

Warning:
2D only.
See also:
preshear()

Definition at line 952 of file Transform.h.

{
  EIGEN_STATIC_ASSERT(int(Dim)==2, YOU_MADE_A_PROGRAMMING_MISTAKE)
  EIGEN_STATIC_ASSERT(Mode!=int(Isometry), THIS_METHOD_IS_ONLY_FOR_SPECIFIC_TRANSFORMATIONS)
  VectorType tmp = linear().col(0)*sy + linear().col(1);
  linear() << linear().col(0) + linear().col(1)*sx, tmp;
  return *this;
}
template<typename Scalar , int Dim, int Mode, int Options>
template<typename OtherDerived >
Transform< Scalar, Dim, Mode, Options > & Eigen::Transform< Scalar, Dim, Mode, Options >::translate ( const MatrixBase< OtherDerived > &  other) [inline]

Applies on the right the translation matrix represented by the vector other to *this and returns a reference to *this.

See also:
pretranslate()

Definition at line 878 of file Transform.h.

{
  EIGEN_STATIC_ASSERT_VECTOR_SPECIFIC_SIZE(OtherDerived,int(Dim))
  translationExt() += linearExt() * other;
  return *this;
}
template<typename _Scalar, int _Dim, int _Mode, int _Options>
ConstTranslationPart Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::translation ( ) const [inline]
Returns:
a read-only expression of the translation vector of the transformation

Definition at line 409 of file Transform.h.

{ return ConstTranslationPart(m_matrix,0,Dim); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
TranslationPart Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::translation ( ) [inline]
Returns:
a writable expression of the translation vector of the transformation

Definition at line 411 of file Transform.h.

{ return TranslationPart(m_matrix,0,Dim); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
Block<MatrixType,int(Mode)==int(Projective)?HDim:Dim,1> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::translationExt ( ) [inline]
Returns:
the translation part if the transformation is affine, and the last column for projective transformations.

Definition at line 654 of file Transform.h.

                                                         :Dim,1> translationExt()
  { return m_matrix.template block<int(Mode)==int(Projective)?HDim:Dim,1>(0,Dim); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
const Block<MatrixType,int(Mode)==int(Projective)?HDim:Dim,1> Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::translationExt ( ) const [inline]
Returns:
the translation part if the transformation is affine, and the last column for projective transformations.

Definition at line 660 of file Transform.h.

                                                               :Dim,1> translationExt() const
  { return m_matrix.template block<int(Mode)==int(Projective)?HDim:Dim,1>(0,Dim); }

Friends And Related Function Documentation

template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename OtherDerived >
const internal::transform_left_product_impl<OtherDerived,Mode,Options,_Dim,_Dim+1>::ResultType operator* ( const EigenBase< OtherDerived > &  a,
const Transform< _Scalar, _Dim, _Mode, _Options > &  b 
) [friend]
Returns:
the product expression of a transformation matrix a times a transform b

The left hand side other can be either:

  • a linear transformation matrix of size Dim x Dim,
  • an affine transformation matrix of size Dim x Dim+1,
  • a general transformation matrix of size Dim+1 x Dim+1.

Definition at line 452 of file Transform.h.

  { return internal::transform_left_product_impl<OtherDerived,Mode,Options,Dim,HDim>::run(a.derived(),b); }
template<typename _Scalar, int _Dim, int _Mode, int _Options>
template<typename DiagonalDerived >
TransformTimeDiagonalReturnType operator* ( const DiagonalBase< DiagonalDerived > &  a,
const Transform< _Scalar, _Dim, _Mode, _Options > &  b 
) [friend]
Returns:
The product expression of a diagonal matrix a times a transform b

The lhs diagonal matrix is interpreted as an affine scaling transformation. The product results in a Transform of the same type (mode) as the lhs only if the lhs mode is no isometry. In that case, the returned transform is an affinity.

Definition at line 478 of file Transform.h.

  {
    TransformTimeDiagonalReturnType res;
    res.linear().noalias() = a*b.linear();
    res.translation().noalias() = a*b.translation();
    if (Mode!=int(AffineCompact))
      res.matrix().row(Dim) = b.matrix().row(Dim);
    return res;
  }

Member Data Documentation

template<typename _Scalar, int _Dim, int _Mode, int _Options>
MatrixType Eigen::Transform< _Scalar, _Dim, _Mode, _Options >::m_matrix [protected]

Definition at line 249 of file Transform.h.

The documentation for this class was generated from the following file:
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Defines