Modified Incomplete Cholesky with dual threshold. More...

#include <IncompleteCholesky.h>

Inheritance diagram for Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >:

Collaboration diagram for Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >:

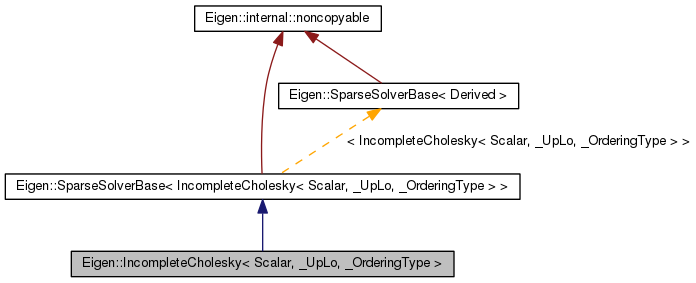
Public Types
enum	{ UpLo = _UpLo }
enum	{ ColsAtCompileTime = Dynamic, MaxColsAtCompileTime = Dynamic }
typedef NumTraits< Scalar >::Real	RealScalar
typedef _OrderingType	OrderingType
typedef OrderingType::PermutationType	PermutationType
typedef PermutationType::StorageIndex	StorageIndex
typedef SparseMatrix< Scalar, ColMajor, StorageIndex >	FactorType
typedef Matrix< Scalar, Dynamic, 1 >	VectorSx
typedef Matrix< RealScalar, Dynamic, 1 >	VectorRx
typedef Matrix< StorageIndex, Dynamic, 1 >	VectorIx
typedef std::vector< std::list < StorageIndex > >	VectorList
Public Member Functions
	IncompleteCholesky ()
template<typename MatrixType >
	IncompleteCholesky (const MatrixType &matrix)
Index	rows () const
Index	cols () const
ComputationInfo	info () const
	Reports whether previous computation was successful.
void	setInitialShift (RealScalar shift)
	Set the initial shift parameter 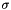$\sigma$ .
template<typename MatrixType >
void	analyzePattern (const MatrixType &mat)
	Computes the fill reducing permutation vector using the sparsity pattern of mat.
template<typename MatrixType >
void	factorize (const MatrixType &mat)
	Performs the numerical factorization of the input matrix mat.
template<typename MatrixType >
void	compute (const MatrixType &mat)
template<typename Rhs , typename Dest >
void	_solve_impl (const Rhs &b, Dest &x) const
const FactorType &	matrixL () const
const VectorRx &	scalingS () const
const PermutationType &	permutationP () const
template<typename _MatrixType >
void	factorize (const _MatrixType &mat)
Protected Types
typedef SparseSolverBase < IncompleteCholesky< Scalar, _UpLo, _OrderingType > >	Base
Protected Attributes
FactorType	m_L
VectorRx	m_scale
RealScalar	m_initialShift
bool	m_analysisIsOk
bool	m_factorizationIsOk
ComputationInfo	m_info
PermutationType	m_perm
Private Member Functions
void	updateList (Ref< const VectorIx > colPtr, Ref< VectorIx > rowIdx, Ref< VectorSx > vals, const Index &col, const Index &jk, VectorIx &firstElt, VectorList &listCol)

Detailed Description

template<typename Scalar, int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>
class Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >

Modified Incomplete Cholesky with dual threshold.

References : C-J. Lin and J. J. Moré, Incomplete Cholesky Factorizations with Limited memory, SIAM J. Sci. Comput. 21(1), pp. 24-45, 1999

Template Parameters:

Scalar	the scalar type of the input matrices
_UpLo	The triangular part that will be used for the computations. It can be Lower or Upper. Default is Lower.
_OrderingType	The ordering method to use, either AMDOrdering<> or NaturalOrdering<>. Default is AMDOrdering<int>, unless EIGEN_MPL2_ONLY is defined, in which case the default is NaturalOrdering<int>.

It performs the following incomplete factorization: 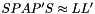$S P A P' S \approx L L'$ where L is a lower triangular factor, S is a diagonal scaling matrix, and P is a fill-in reducing permutation as computed by the ordering method.

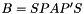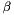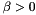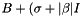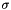Shifting strategy: Let $ B = S P A P' S $ be the scaled matrix on which the factorization is carried out, and $\beta$ be the minimum value of the diagonal. If $\beta > 0$ then, the factorization is directly performed on the matrix B. Otherwise, the factorization is performed on the shifted matrix $B + (\sigma+|\beta| I$ where $\sigma$ is the initial shift value as returned and set by setInitialShift() method. The default value is 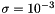$\sigma = 10^{-3}$ . If the factorization fails, then the shift in doubled until it succeed or a maximum of ten attempts. If it still fails, as returned by the info() method, then you can either increase the initial shift, or better use another preconditioning technique.

Definition at line 51 of file IncompleteCholesky.h.

Member Typedef Documentation

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

typedef SparseSolverBase<IncompleteCholesky<Scalar,_UpLo,_OrderingType> > Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::Base [protected]

Definition at line 54 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

typedef SparseMatrix<Scalar,ColMajor,StorageIndex> Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::FactorType

Definition at line 61 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

typedef _OrderingType Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::OrderingType

Definition at line 58 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

typedef OrderingType::PermutationType Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::PermutationType

Definition at line 59 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

typedef NumTraits<Scalar>::Real Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::RealScalar

Definition at line 57 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

typedef PermutationType::StorageIndex Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::StorageIndex

Definition at line 60 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

typedef Matrix<StorageIndex,Dynamic, 1> Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::VectorIx

Definition at line 64 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

typedef std::vector<std::list<StorageIndex> > Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::VectorList

Definition at line 65 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

typedef Matrix<RealScalar,Dynamic,1> Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::VectorRx

Definition at line 63 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

typedef Matrix<Scalar,Dynamic,1> Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::VectorSx

Definition at line 62 of file IncompleteCholesky.h.

Member Enumeration Documentation

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

anonymous enum

Enumerator:

UpLo

Definition at line 66 of file IncompleteCholesky.h.

{ UpLo = _UpLo };

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

anonymous enum

Enumerator:

ColsAtCompileTime
MaxColsAtCompileTime

Definition at line 67 of file IncompleteCholesky.h.

         {
      ColsAtCompileTime = Dynamic,
      MaxColsAtCompileTime = Dynamic
    };

Constructor & Destructor Documentation

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::IncompleteCholesky ( ) [inline]

Default constructor leaving the object in a partly non-initialized stage.

You must call compute() or the pair analyzePattern()/factorize() to make it valid.

See also:: IncompleteCholesky(const MatrixType&)

Definition at line 79 of file IncompleteCholesky.h.

: m_initialShift(1e-3),m_factorizationIsOk(false) {}

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

template<typename MatrixType >

Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::IncompleteCholesky ( const MatrixType & matrix ) [inline]

Constructor computing the incomplete factorization for the given matrix matrix.

Definition at line 84 of file IncompleteCholesky.h.

                                                 : m_initialShift(1e-3),m_factorizationIsOk(false)
    {
      compute(matrix);
    }

Member Function Documentation

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

template<typename Rhs , typename Dest >

void Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::_solve_impl	(	const Rhs &	b,
		Dest &	x
	)		const `[inline]`

Definition at line 155 of file IncompleteCholesky.h.

    {
      eigen_assert(m_factorizationIsOk && "factorize() should be called first");
      if (m_perm.rows() == b.rows())  x = m_perm * b;
      else                            x = b;
      x = m_scale.asDiagonal() * x;
      x = m_L.template triangularView<Lower>().solve(x);
      x = m_L.adjoint().template triangularView<Upper>().solve(x);
      x = m_scale.asDiagonal() * x;
      if (m_perm.rows() == b.rows())
        x = m_perm.inverse() * x;
    }

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

template<typename MatrixType >

void Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::analyzePattern ( const MatrixType & mat ) [inline]

Computes the fill reducing permutation vector using the sparsity pattern of mat.

Definition at line 117 of file IncompleteCholesky.h.

    {
      OrderingType ord; 
      PermutationType pinv;
      ord(mat.template selfadjointView<UpLo>(), pinv); 
      if(pinv.size()>0) m_perm = pinv.inverse();
      else              m_perm.resize(0);
      m_L.resize(mat.rows(), mat.cols());
      m_analysisIsOk = true;
      m_isInitialized = true;
      m_info = Success;
    }

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

Index Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::cols ( void ) const [inline]

Returns:: number of columns of the factored matrix

Definition at line 93 of file IncompleteCholesky.h.

{ return m_L.cols(); }

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

template<typename MatrixType >

void Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::compute ( const MatrixType & mat ) [inline]

Computes or re-computes the incomplete Cholesky factorization of the input matrix mat

It is a shortcut for a sequential call to the analyzePattern() and factorize() methods.

See also:: analyzePattern(), factorize()

Definition at line 147 of file IncompleteCholesky.h.

    {
      analyzePattern(mat);
      factorize(mat);
    }

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

template<typename MatrixType >

void Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::factorize ( const MatrixType & mat )

Performs the numerical factorization of the input matrix mat.

The method analyzePattern() or compute() must have been called beforehand with a matrix having the same pattern.

See also:: compute(), analyzePattern()

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

template<typename _MatrixType >

void Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::factorize ( const _MatrixType & mat )

Definition at line 196 of file IncompleteCholesky.h.

{
  using std::sqrt;
  eigen_assert(m_analysisIsOk && "analyzePattern() should be called first"); 
    
  // Dropping strategy : Keep only the p largest elements per column, where p is the number of elements in the column of the original matrix. Other strategies will be added
  
  // Apply the fill-reducing permutation computed in analyzePattern()
  if (m_perm.rows() == mat.rows() ) // To detect the null permutation
  {
    // The temporary is needed to make sure that the diagonal entry is properly sorted
    FactorType tmp(mat.rows(), mat.cols());
    tmp = mat.template selfadjointView<_UpLo>().twistedBy(m_perm);
    m_L.template selfadjointView<Lower>() = tmp.template selfadjointView<Lower>();
  }
  else
  {
    m_L.template selfadjointView<Lower>() = mat.template selfadjointView<_UpLo>();
  }
  
  Index n = m_L.cols(); 
  Index nnz = m_L.nonZeros();
  Map<VectorSx> vals(m_L.valuePtr(), nnz);         //values
  Map<VectorIx> rowIdx(m_L.innerIndexPtr(), nnz);  //Row indices
  Map<VectorIx> colPtr( m_L.outerIndexPtr(), n+1); // Pointer to the beginning of each row
  VectorIx firstElt(n-1); // for each j, points to the next entry in vals that will be used in the factorization
  VectorList listCol(n);  // listCol(j) is a linked list of columns to update column j
  VectorSx col_vals(n);   // Store a  nonzero values in each column
  VectorIx col_irow(n);   // Row indices of nonzero elements in each column
  VectorIx col_pattern(n);
  col_pattern.fill(-1);
  StorageIndex col_nnz;
  
  
  // Computes the scaling factors 
  m_scale.resize(n);
  m_scale.setZero();
  for (Index j = 0; j < n; j++)
    for (Index k = colPtr[j]; k < colPtr[j+1]; k++)
    {
      m_scale(j) += numext::abs2(vals(k));
      if(rowIdx[k]!=j)
        m_scale(rowIdx[k]) += numext::abs2(vals(k));
    }
  
  m_scale = m_scale.cwiseSqrt().cwiseSqrt();

  for (Index j = 0; j < n; ++j)
    if(m_scale(j)>(std::numeric_limits<RealScalar>::min)())
      m_scale(j) = RealScalar(1)/m_scale(j);
    else
      m_scale(j) = 1;

  // TODO disable scaling if not needed, i.e., if it is roughly uniform? (this will make solve() faster)
  
  // Scale and compute the shift for the matrix 
  RealScalar mindiag = NumTraits<RealScalar>::highest();
  for (Index j = 0; j < n; j++)
  {
    for (Index k = colPtr[j]; k < colPtr[j+1]; k++)
      vals[k] *= (m_scale(j)*m_scale(rowIdx[k]));
    eigen_internal_assert(rowIdx[colPtr[j]]==j && "IncompleteCholesky: only the lower triangular part must be stored");
    mindiag = numext::mini(numext::real(vals[colPtr[j]]), mindiag);
  }

  FactorType L_save = m_L;
  
  RealScalar shift = 0;
  if(mindiag <= RealScalar(0.))
    shift = m_initialShift - mindiag;

  m_info = NumericalIssue;

  // Try to perform the incomplete factorization using the current shift
  int iter = 0;
  do
  {
    // Apply the shift to the diagonal elements of the matrix
    for (Index j = 0; j < n; j++)
      vals[colPtr[j]] += shift;

    // jki version of the Cholesky factorization
    Index j=0;
    for (; j < n; ++j)
    {
      // Left-looking factorization of the j-th column
      // First, load the j-th column into col_vals
      Scalar diag = vals[colPtr[j]];  // It is assumed that only the lower part is stored
      col_nnz = 0;
      for (Index i = colPtr[j] + 1; i < colPtr[j+1]; i++)
      {
        StorageIndex l = rowIdx[i];
        col_vals(col_nnz) = vals[i];
        col_irow(col_nnz) = l;
        col_pattern(l) = col_nnz;
        col_nnz++;
      }
      {
        typename std::list<StorageIndex>::iterator k;
        // Browse all previous columns that will update column j
        for(k = listCol[j].begin(); k != listCol[j].end(); k++)
        {
          Index jk = firstElt(*k); // First element to use in the column
          eigen_internal_assert(rowIdx[jk]==j);
          Scalar v_j_jk = numext::conj(vals[jk]);

          jk += 1;
          for (Index i = jk; i < colPtr[*k+1]; i++)
          {
            StorageIndex l = rowIdx[i];
            if(col_pattern[l]<0)
            {
              col_vals(col_nnz) = vals[i] * v_j_jk;
              col_irow[col_nnz] = l;
              col_pattern(l) = col_nnz;
              col_nnz++;
            }
            else
              col_vals(col_pattern[l]) -= vals[i] * v_j_jk;
          }
          updateList(colPtr,rowIdx,vals, *k, jk, firstElt, listCol);
        }
      }

      // Scale the current column
      if(numext::real(diag) <= 0)
      {
        if(++iter>=10)
          return;

        // increase shift
        shift = numext::maxi(m_initialShift,RealScalar(2)*shift);
        // restore m_L, col_pattern, and listCol
        vals = Map<const VectorSx>(L_save.valuePtr(), nnz);
        rowIdx = Map<const VectorIx>(L_save.innerIndexPtr(), nnz);
        colPtr = Map<const VectorIx>(L_save.outerIndexPtr(), n+1);
        col_pattern.fill(-1);
        for(Index i=0; i<n; ++i)
          listCol[i].clear();

        break;
      }

      RealScalar rdiag = sqrt(numext::real(diag));
      vals[colPtr[j]] = rdiag;
      for (Index k = 0; k<col_nnz; ++k)
      {
        Index i = col_irow[k];
        //Scale
        col_vals(k) /= rdiag;
        //Update the remaining diagonals with col_vals
        vals[colPtr[i]] -= numext::abs2(col_vals(k));
      }
      // Select the largest p elements
      // p is the original number of elements in the column (without the diagonal)
      Index p = colPtr[j+1] - colPtr[j] - 1 ;
      Ref<VectorSx> cvals = col_vals.head(col_nnz);
      Ref<VectorIx> cirow = col_irow.head(col_nnz);
      internal::QuickSplit(cvals,cirow, p);
      // Insert the largest p elements in the matrix
      Index cpt = 0;
      for (Index i = colPtr[j]+1; i < colPtr[j+1]; i++)
      {
        vals[i] = col_vals(cpt);
        rowIdx[i] = col_irow(cpt);
        // restore col_pattern:
        col_pattern(col_irow(cpt)) = -1;
        cpt++;
      }
      // Get the first smallest row index and put it after the diagonal element
      Index jk = colPtr(j)+1;
      updateList(colPtr,rowIdx,vals,j,jk,firstElt,listCol);
    }

    if(j==n)
    {
      m_factorizationIsOk = true;
      m_info = Success;
    }
  } while(m_info!=Success);
}

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

ComputationInfo Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::info ( ) const [inline]

Reports whether previous computation was successful.

It triggers an assertion if *this has not been initialized through the respective constructor, or a call to compute() or analyzePattern().

Returns:: Success if computation was successful, NumericalIssue if the matrix appears to be negative.

Definition at line 104 of file IncompleteCholesky.h.

    {
      eigen_assert(m_isInitialized && "IncompleteCholesky is not initialized.");
      return m_info;
    }

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

const FactorType& Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::matrixL ( ) const [inline]

Returns:: the sparse lower triangular factor L

Definition at line 169 of file IncompleteCholesky.h.

{ eigen_assert("m_factorizationIsOk"); return m_L; }

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

const PermutationType& Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::permutationP ( ) const [inline]

Returns:: the fill-in reducing permutation P (can be empty for a natural ordering)

Definition at line 175 of file IncompleteCholesky.h.

{ eigen_assert("m_analysisIsOk"); return m_perm; }

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

Index Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::rows ( void ) const [inline]

Returns:: number of rows of the factored matrix

Definition at line 90 of file IncompleteCholesky.h.

{ return m_L.rows(); }

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

const VectorRx& Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::scalingS ( ) const [inline]

Returns:: a vector representing the scaling factor S

Definition at line 172 of file IncompleteCholesky.h.

{ eigen_assert("m_factorizationIsOk"); return m_scale; }

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

void Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::setInitialShift ( RealScalar shift ) [inline]

Set the initial shift parameter 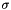$\sigma$ .

Definition at line 112 of file IncompleteCholesky.h.

{ m_initialShift = shift; }

template<typename Scalar , int _UpLo, typename OrderingType >

void Eigen::IncompleteCholesky< Scalar, _UpLo, OrderingType >::updateList	(	Ref< const VectorIx >	colPtr,
		Ref< VectorIx >	rowIdx,
		Ref< VectorSx >	vals,
		const Index &	col,
		const Index &	jk,
		VectorIx &	firstElt,
		VectorList &	listCol
	)		`[inline, private]`

Definition at line 379 of file IncompleteCholesky.h.

{
  if (jk < colPtr(col+1) )
  {
    Index p = colPtr(col+1) - jk;
    Index minpos; 
    rowIdx.segment(jk,p).minCoeff(&minpos);
    minpos += jk;
    if (rowIdx(minpos) != rowIdx(jk))
    {
      //Swap
      std::swap(rowIdx(jk),rowIdx(minpos));
      std::swap(vals(jk),vals(minpos));
    }
    firstElt(col) = internal::convert_index<StorageIndex,Index>(jk);
    listCol[rowIdx(jk)].push_back(internal::convert_index<StorageIndex,Index>(col));
  }
}

Member Data Documentation

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

bool Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::m_analysisIsOk [protected]

Definition at line 181 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

bool Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::m_factorizationIsOk [protected]

Definition at line 182 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

ComputationInfo Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::m_info [protected]

Definition at line 183 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

RealScalar Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::m_initialShift [protected]

Definition at line 180 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

FactorType Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::m_L [protected]

Definition at line 178 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

PermutationType Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::m_perm [protected]

Definition at line 184 of file IncompleteCholesky.h.

template<typename Scalar , int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>

VectorRx Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >::m_scale [protected]

Definition at line 179 of file IncompleteCholesky.h.

The documentation for this class was generated from the following file:

IncompleteCholesky.h

Public Types

Public Member Functions

Protected Types

Protected Attributes

Private Member Functions

Detailed Description

template<typename Scalar, int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>> class Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >

Member Typedef Documentation

Member Enumeration Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<typename Scalar, int _UpLo = Lower, typename _OrderingType = AMDOrdering<int>>
class Eigen::IncompleteCholesky< Scalar, _UpLo, _OrderingType >