|
MOAB
4.9.3pre
|
|
MOAB
4.9.3pre
|
Incomplete LU factorization with dual-threshold strategy. More...
#include <IncompleteLUT.h>

Classes | |
| struct | keep_diag |
Public Types | |
| enum | { ColsAtCompileTime = Dynamic, MaxColsAtCompileTime = Dynamic } |
| typedef _Scalar | Scalar |
| typedef _StorageIndex | StorageIndex |
| typedef NumTraits< Scalar >::Real | RealScalar |
| typedef Matrix< Scalar, Dynamic, 1 > | Vector |
| typedef Matrix< StorageIndex, Dynamic, 1 > | VectorI |
| typedef SparseMatrix< Scalar, RowMajor, StorageIndex > | FactorType |
Public Member Functions | |
| IncompleteLUT () | |
| template<typename MatrixType > | |
| IncompleteLUT (const MatrixType &mat, const RealScalar &droptol=NumTraits< Scalar >::dummy_precision(), int fillfactor=10) | |
| Index | rows () const |
| Index | cols () const |
| ComputationInfo | info () const |
| Reports whether previous computation was successful. | |
| template<typename MatrixType > | |
| void | analyzePattern (const MatrixType &amat) |
| template<typename MatrixType > | |
| void | factorize (const MatrixType &amat) |
| template<typename MatrixType > | |
| IncompleteLUT & | compute (const MatrixType &amat) |
| void | setDroptol (const RealScalar &droptol) |
| void | setFillfactor (int fillfactor) |
| template<typename Rhs , typename Dest > | |
| void | _solve_impl (const Rhs &b, Dest &x) const |
| template<typename _MatrixType > | |
| void | analyzePattern (const _MatrixType &amat) |
| template<typename _MatrixType > | |
| void | factorize (const _MatrixType &amat) |
Protected Types | |
| typedef SparseSolverBase < IncompleteLUT > | Base |
Protected Attributes | |
| FactorType | m_lu |
| RealScalar | m_droptol |
| int | m_fillfactor |
| bool | m_analysisIsOk |
| bool | m_factorizationIsOk |
| ComputationInfo | m_info |
| PermutationMatrix< Dynamic, Dynamic, StorageIndex > | m_P |
| PermutationMatrix< Dynamic, Dynamic, StorageIndex > | m_Pinv |
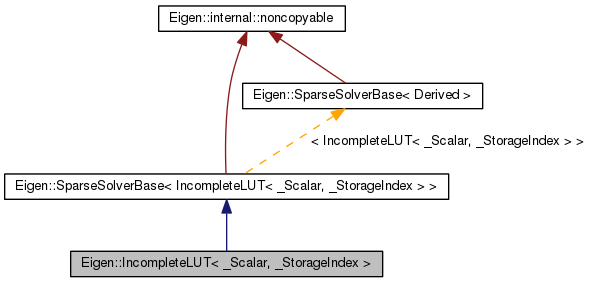
Incomplete LU factorization with dual-threshold strategy.
During the numerical factorization, two dropping rules are used : 1) any element whose magnitude is less than some tolerance is dropped. This tolerance is obtained by multiplying the input tolerance droptol by the average magnitude of all the original elements in the current row. 2) After the elimination of the row, only the fill largest elements in the L part and the fill largest elements in the U part are kept (in addition to the diagonal element ). Note that fill is computed from the input parameter fillfactor which is used the ratio to control the fill_in relatively to the initial number of nonzero elements.
The two extreme cases are when droptol=0 (to keep all the fill*2 largest elements) and when fill=n/2 with droptol being different to zero.
References : Yousef Saad, ILUT: A dual threshold incomplete LU factorization, Numerical Linear Algebra with Applications, 1(4), pp 387-402, 1994.
NOTE : The following implementation is derived from the ILUT implementation in the SPARSKIT package, Copyright (C) 2005, the Regents of the University of Minnesota released under the terms of the GNU LGPL: http://www-users.cs.umn.edu/~saad/software/SPARSKIT/README However, Yousef Saad gave us permission to relicense his ILUT code to MPL2. See the Eigen mailing list archive, thread: ILUT, date: July 8, 2012: http://listengine.tuxfamily.org/lists.tuxfamily.org/eigen/2012/07/msg00064.html alternatively, on GMANE: http://comments.gmane.org/gmane.comp.lib.eigen/3302
Definition at line 99 of file IncompleteLUT.h.
typedef SparseSolverBase<IncompleteLUT> Eigen::IncompleteLUT< _Scalar, _StorageIndex >::Base [protected] |
Definition at line 102 of file IncompleteLUT.h.
| typedef SparseMatrix<Scalar,RowMajor,StorageIndex> Eigen::IncompleteLUT< _Scalar, _StorageIndex >::FactorType |
Definition at line 110 of file IncompleteLUT.h.
| typedef NumTraits<Scalar>::Real Eigen::IncompleteLUT< _Scalar, _StorageIndex >::RealScalar |
Definition at line 107 of file IncompleteLUT.h.
| typedef _Scalar Eigen::IncompleteLUT< _Scalar, _StorageIndex >::Scalar |
Definition at line 105 of file IncompleteLUT.h.
| typedef _StorageIndex Eigen::IncompleteLUT< _Scalar, _StorageIndex >::StorageIndex |
Definition at line 106 of file IncompleteLUT.h.
| typedef Matrix<Scalar,Dynamic,1> Eigen::IncompleteLUT< _Scalar, _StorageIndex >::Vector |
Definition at line 108 of file IncompleteLUT.h.
| typedef Matrix<StorageIndex,Dynamic,1> Eigen::IncompleteLUT< _Scalar, _StorageIndex >::VectorI |
Definition at line 109 of file IncompleteLUT.h.
| anonymous enum |
Definition at line 112 of file IncompleteLUT.h.
{
ColsAtCompileTime = Dynamic,
MaxColsAtCompileTime = Dynamic
};
| Eigen::IncompleteLUT< _Scalar, _StorageIndex >::IncompleteLUT | ( | ) | [inline] |
Definition at line 119 of file IncompleteLUT.h.
: m_droptol(NumTraits<Scalar>::dummy_precision()), m_fillfactor(10), m_analysisIsOk(false), m_factorizationIsOk(false) {}
| Eigen::IncompleteLUT< _Scalar, _StorageIndex >::IncompleteLUT | ( | const MatrixType & | mat, |
| const RealScalar & | droptol = NumTraits<Scalar>::dummy_precision(), |
||
| int | fillfactor = 10 |
||
| ) | [inline, explicit] |
Definition at line 125 of file IncompleteLUT.h.
: m_droptol(droptol),m_fillfactor(fillfactor), m_analysisIsOk(false),m_factorizationIsOk(false) { eigen_assert(fillfactor != 0); compute(mat); }
| void Eigen::IncompleteLUT< _Scalar, _StorageIndex >::_solve_impl | ( | const Rhs & | b, |
| Dest & | x | ||
| ) | const [inline] |
| void Eigen::IncompleteLUT< _Scalar, _StorageIndex >::analyzePattern | ( | const MatrixType & | amat | ) |
| void Eigen::IncompleteLUT< _Scalar, _StorageIndex >::analyzePattern | ( | const _MatrixType & | amat | ) |
Definition at line 223 of file IncompleteLUT.h.
{
// Compute the Fill-reducing permutation
// Since ILUT does not perform any numerical pivoting,
// it is highly preferable to keep the diagonal through symmetric permutations.
#ifndef EIGEN_MPL2_ONLY
// To this end, let's symmetrize the pattern and perform AMD on it.
SparseMatrix<Scalar,ColMajor, StorageIndex> mat1 = amat;
SparseMatrix<Scalar,ColMajor, StorageIndex> mat2 = amat.transpose();
// FIXME for a matrix with nearly symmetric pattern, mat2+mat1 is the appropriate choice.
// on the other hand for a really non-symmetric pattern, mat2*mat1 should be prefered...
SparseMatrix<Scalar,ColMajor, StorageIndex> AtA = mat2 + mat1;
AMDOrdering<StorageIndex> ordering;
ordering(AtA,m_P);
m_Pinv = m_P.inverse(); // cache the inverse permutation
#else
// If AMD is not available, (MPL2-only), then let's use the slower COLAMD routine.
SparseMatrix<Scalar,ColMajor, StorageIndex> mat1 = amat;
COLAMDOrdering<StorageIndex> ordering;
ordering(mat1,m_Pinv);
m_P = m_Pinv.inverse();
#endif
m_analysisIsOk = true;
m_factorizationIsOk = false;
m_isInitialized = true;
}
| Index Eigen::IncompleteLUT< _Scalar, _StorageIndex >::cols | ( | void | ) | const [inline] |
Definition at line 135 of file IncompleteLUT.h.
| IncompleteLUT& Eigen::IncompleteLUT< _Scalar, _StorageIndex >::compute | ( | const MatrixType & | amat | ) | [inline] |
Compute an incomplete LU factorization with dual threshold on the matrix mat No pivoting is done in this version
Definition at line 160 of file IncompleteLUT.h.
{
analyzePattern(amat);
factorize(amat);
return *this;
}
| void Eigen::IncompleteLUT< _Scalar, _StorageIndex >::factorize | ( | const MatrixType & | amat | ) |
| void Eigen::IncompleteLUT< _Scalar, _StorageIndex >::factorize | ( | const _MatrixType & | amat | ) |
Definition at line 253 of file IncompleteLUT.h.
{
using std::sqrt;
using std::swap;
using std::abs;
using internal::convert_index;
eigen_assert((amat.rows() == amat.cols()) && "The factorization should be done on a square matrix");
Index n = amat.cols(); // Size of the matrix
m_lu.resize(n,n);
// Declare Working vectors and variables
Vector u(n) ; // real values of the row -- maximum size is n --
VectorI ju(n); // column position of the values in u -- maximum size is n
VectorI jr(n); // Indicate the position of the nonzero elements in the vector u -- A zero location is indicated by -1
// Apply the fill-reducing permutation
eigen_assert(m_analysisIsOk && "You must first call analyzePattern()");
SparseMatrix<Scalar,RowMajor, StorageIndex> mat;
mat = amat.twistedBy(m_Pinv);
// Initialization
jr.fill(-1);
ju.fill(0);
u.fill(0);
// number of largest elements to keep in each row:
Index fill_in = (amat.nonZeros()*m_fillfactor)/n + 1;
if (fill_in > n) fill_in = n;
// number of largest nonzero elements to keep in the L and the U part of the current row:
Index nnzL = fill_in/2;
Index nnzU = nnzL;
m_lu.reserve(n * (nnzL + nnzU + 1));
// global loop over the rows of the sparse matrix
for (Index ii = 0; ii < n; ii++)
{
// 1 - copy the lower and the upper part of the row i of mat in the working vector u
Index sizeu = 1; // number of nonzero elements in the upper part of the current row
Index sizel = 0; // number of nonzero elements in the lower part of the current row
ju(ii) = convert_index<StorageIndex>(ii);
u(ii) = 0;
jr(ii) = convert_index<StorageIndex>(ii);
RealScalar rownorm = 0;
typename FactorType::InnerIterator j_it(mat, ii); // Iterate through the current row ii
for (; j_it; ++j_it)
{
Index k = j_it.index();
if (k < ii)
{
// copy the lower part
ju(sizel) = convert_index<StorageIndex>(k);
u(sizel) = j_it.value();
jr(k) = convert_index<StorageIndex>(sizel);
++sizel;
}
else if (k == ii)
{
u(ii) = j_it.value();
}
else
{
// copy the upper part
Index jpos = ii + sizeu;
ju(jpos) = convert_index<StorageIndex>(k);
u(jpos) = j_it.value();
jr(k) = convert_index<StorageIndex>(jpos);
++sizeu;
}
rownorm += numext::abs2(j_it.value());
}
// 2 - detect possible zero row
if(rownorm==0)
{
m_info = NumericalIssue;
return;
}
// Take the 2-norm of the current row as a relative tolerance
rownorm = sqrt(rownorm);
// 3 - eliminate the previous nonzero rows
Index jj = 0;
Index len = 0;
while (jj < sizel)
{
// In order to eliminate in the correct order,
// we must select first the smallest column index among ju(jj:sizel)
Index k;
Index minrow = ju.segment(jj,sizel-jj).minCoeff(&k); // k is relative to the segment
k += jj;
if (minrow != ju(jj))
{
// swap the two locations
Index j = ju(jj);
swap(ju(jj), ju(k));
jr(minrow) = convert_index<StorageIndex>(jj);
jr(j) = convert_index<StorageIndex>(k);
swap(u(jj), u(k));
}
// Reset this location
jr(minrow) = -1;
// Start elimination
typename FactorType::InnerIterator ki_it(m_lu, minrow);
while (ki_it && ki_it.index() < minrow) ++ki_it;
eigen_internal_assert(ki_it && ki_it.col()==minrow);
Scalar fact = u(jj) / ki_it.value();
// drop too small elements
if(abs(fact) <= m_droptol)
{
jj++;
continue;
}
// linear combination of the current row ii and the row minrow
++ki_it;
for (; ki_it; ++ki_it)
{
Scalar prod = fact * ki_it.value();
Index j = ki_it.index();
Index jpos = jr(j);
if (jpos == -1) // fill-in element
{
Index newpos;
if (j >= ii) // dealing with the upper part
{
newpos = ii + sizeu;
sizeu++;
eigen_internal_assert(sizeu<=n);
}
else // dealing with the lower part
{
newpos = sizel;
sizel++;
eigen_internal_assert(sizel<=ii);
}
ju(newpos) = convert_index<StorageIndex>(j);
u(newpos) = -prod;
jr(j) = convert_index<StorageIndex>(newpos);
}
else
u(jpos) -= prod;
}
// store the pivot element
u(len) = fact;
ju(len) = convert_index<StorageIndex>(minrow);
++len;
jj++;
} // end of the elimination on the row ii
// reset the upper part of the pointer jr to zero
for(Index k = 0; k <sizeu; k++) jr(ju(ii+k)) = -1;
// 4 - partially sort and insert the elements in the m_lu matrix
// sort the L-part of the row
sizel = len;
len = (std::min)(sizel, nnzL);
typename Vector::SegmentReturnType ul(u.segment(0, sizel));
typename VectorI::SegmentReturnType jul(ju.segment(0, sizel));
internal::QuickSplit(ul, jul, len);
// store the largest m_fill elements of the L part
m_lu.startVec(ii);
for(Index k = 0; k < len; k++)
m_lu.insertBackByOuterInnerUnordered(ii,ju(k)) = u(k);
// store the diagonal element
// apply a shifting rule to avoid zero pivots (we are doing an incomplete factorization)
if (u(ii) == Scalar(0))
u(ii) = sqrt(m_droptol) * rownorm;
m_lu.insertBackByOuterInnerUnordered(ii, ii) = u(ii);
// sort the U-part of the row
// apply the dropping rule first
len = 0;
for(Index k = 1; k < sizeu; k++)
{
if(abs(u(ii+k)) > m_droptol * rownorm )
{
++len;
u(ii + len) = u(ii + k);
ju(ii + len) = ju(ii + k);
}
}
sizeu = len + 1; // +1 to take into account the diagonal element
len = (std::min)(sizeu, nnzU);
typename Vector::SegmentReturnType uu(u.segment(ii+1, sizeu-1));
typename VectorI::SegmentReturnType juu(ju.segment(ii+1, sizeu-1));
internal::QuickSplit(uu, juu, len);
// store the largest elements of the U part
for(Index k = ii + 1; k < ii + len; k++)
m_lu.insertBackByOuterInnerUnordered(ii,ju(k)) = u(k);
}
m_lu.finalize();
m_lu.makeCompressed();
m_factorizationIsOk = true;
m_info = Success;
}
| ComputationInfo Eigen::IncompleteLUT< _Scalar, _StorageIndex >::info | ( | ) | const [inline] |
Reports whether previous computation was successful.
Success if computation was succesful, NumericalIssue if the matrix.appears to be negative. Definition at line 142 of file IncompleteLUT.h.
{
eigen_assert(m_isInitialized && "IncompleteLUT is not initialized.");
return m_info;
}
| Index Eigen::IncompleteLUT< _Scalar, _StorageIndex >::rows | ( | void | ) | const [inline] |
Definition at line 133 of file IncompleteLUT.h.
| void Eigen::IncompleteLUT< Scalar, StorageIndex >::setDroptol | ( | const RealScalar & | droptol | ) |
Set control parameter droptol
| droptol | Drop any element whose magnitude is less than this tolerance |
Definition at line 206 of file IncompleteLUT.h.
{
this->m_droptol = droptol;
}
| void Eigen::IncompleteLUT< Scalar, StorageIndex >::setFillfactor | ( | int | fillfactor | ) |
Set control parameter fillfactor
| fillfactor | This is used to compute the number fill_in of largest elements to keep on each row. |
Definition at line 216 of file IncompleteLUT.h.
{
this->m_fillfactor = fillfactor;
}
bool Eigen::IncompleteLUT< _Scalar, _StorageIndex >::m_analysisIsOk [protected] |
Definition at line 194 of file IncompleteLUT.h.
RealScalar Eigen::IncompleteLUT< _Scalar, _StorageIndex >::m_droptol [protected] |
Definition at line 192 of file IncompleteLUT.h.
bool Eigen::IncompleteLUT< _Scalar, _StorageIndex >::m_factorizationIsOk [protected] |
Definition at line 195 of file IncompleteLUT.h.
int Eigen::IncompleteLUT< _Scalar, _StorageIndex >::m_fillfactor [protected] |
Definition at line 193 of file IncompleteLUT.h.
ComputationInfo Eigen::IncompleteLUT< _Scalar, _StorageIndex >::m_info [protected] |
Definition at line 196 of file IncompleteLUT.h.
FactorType Eigen::IncompleteLUT< _Scalar, _StorageIndex >::m_lu [protected] |
Definition at line 191 of file IncompleteLUT.h.
PermutationMatrix<Dynamic,Dynamic,StorageIndex> Eigen::IncompleteLUT< _Scalar, _StorageIndex >::m_P [protected] |
Definition at line 197 of file IncompleteLUT.h.
PermutationMatrix<Dynamic,Dynamic,StorageIndex> Eigen::IncompleteLUT< _Scalar, _StorageIndex >::m_Pinv [protected] |
Definition at line 198 of file IncompleteLUT.h.