Standard Cholesky decomposition (LL^T) of a matrix and associated features. More...

#include <LLT.h>

Public Types
enum	{ RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, Options = MatrixType::Options, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }
enum	{ PacketSize = internal::packet_traits<Scalar>::size, AlignmentMask = int(PacketSize)-1, UpLo = _UpLo }
typedef _MatrixType	MatrixType
typedef MatrixType::Scalar	Scalar
typedef NumTraits< typename MatrixType::Scalar >::Real	RealScalar
typedef Eigen::Index	Index
typedef MatrixType::StorageIndex	StorageIndex
typedef internal::LLT_Traits < MatrixType, UpLo >	Traits
Public Member Functions
	LLT ()
	Default Constructor.
	LLT (Index size)
	Default Constructor with memory preallocation.
template<typename InputType >
	LLT (const EigenBase< InputType > &matrix)
Traits::MatrixU	matrixU () const
Traits::MatrixL	matrixL () const
template<typename Rhs >
const Solve< LLT, Rhs >	solve (const MatrixBase< Rhs > &b) const
template<typename Derived >
void	solveInPlace (MatrixBase< Derived > &bAndX) const
template<typename InputType >
LLT &	compute (const EigenBase< InputType > &matrix)
const MatrixType &	matrixLLT () const
MatrixType	reconstructedMatrix () const
ComputationInfo	info () const
	Reports whether previous computation was successful.
Index	rows () const
Index	cols () const
template<typename VectorType >
LLT	rankUpdate (const VectorType &vec, const RealScalar &sigma=1)
template<typename RhsType , typename DstType >
EIGEN_DEVICE_FUNC void	_solve_impl (const RhsType &rhs, DstType &dst) const
Static Protected Member Functions
static void	check_template_parameters ()
Protected Attributes
MatrixType	m_matrix
bool	m_isInitialized
ComputationInfo	m_info

Detailed Description

template<typename _MatrixType, int _UpLo>
class Eigen::LLT< _MatrixType, _UpLo >

Standard Cholesky decomposition (LL^T) of a matrix and associated features.

Template Parameters:

_MatrixType	the type of the matrix of which we are computing the LL^T Cholesky decomposition
_UpLo	the triangular part that will be used for the decompositon: Lower (default) or Upper. The other triangular part won't be read.

This class performs a LL^T Cholesky decomposition of a symmetric, positive definite matrix A such that A = LL^* = U^*U, where L is lower triangular.

While the Cholesky decomposition is particularly useful to solve selfadjoint problems like D^*D x = b, for that purpose, we recommend the Cholesky decomposition without square root which is more stable and even faster. Nevertheless, this standard Cholesky decomposition remains useful in many other situations like generalised eigen problems with hermitian matrices.

Remember that Cholesky decompositions are not rank-revealing. This LLT decomposition is only stable on positive definite matrices, use LDLT instead for the semidefinite case. Also, do not use a Cholesky decomposition to determine whether a system of equations has a solution.

Example:

Output:

See also:: MatrixBase::llt(), SelfAdjointView::llt(), class LDLT

Definition at line 50 of file LLT.h.

Member Typedef Documentation

template<typename _MatrixType, int _UpLo>

typedef Eigen::Index Eigen::LLT< _MatrixType, _UpLo >::Index

Deprecated:: since Eigen 3.3

Definition at line 62 of file LLT.h.

template<typename _MatrixType, int _UpLo>

typedef _MatrixType Eigen::LLT< _MatrixType, _UpLo >::MatrixType

Definition at line 53 of file LLT.h.

template<typename _MatrixType, int _UpLo>

typedef NumTraits<typename MatrixType::Scalar>::Real Eigen::LLT< _MatrixType, _UpLo >::RealScalar

Definition at line 61 of file LLT.h.

template<typename _MatrixType, int _UpLo>

typedef MatrixType::Scalar Eigen::LLT< _MatrixType, _UpLo >::Scalar

Definition at line 60 of file LLT.h.

template<typename _MatrixType, int _UpLo>

typedef MatrixType::StorageIndex Eigen::LLT< _MatrixType, _UpLo >::StorageIndex

Definition at line 63 of file LLT.h.

template<typename _MatrixType, int _UpLo>

typedef internal::LLT_Traits<MatrixType,UpLo> Eigen::LLT< _MatrixType, _UpLo >::Traits

Definition at line 71 of file LLT.h.

Member Enumeration Documentation

template<typename _MatrixType, int _UpLo>

anonymous enum

Enumerator:

RowsAtCompileTime
ColsAtCompileTime
Options
MaxColsAtCompileTime

Definition at line 54 of file LLT.h.

         {
      RowsAtCompileTime = MatrixType::RowsAtCompileTime,
      ColsAtCompileTime = MatrixType::ColsAtCompileTime,
      Options = MatrixType::Options,
      MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime
    };

template<typename _MatrixType, int _UpLo>

anonymous enum

Enumerator:

PacketSize
AlignmentMask
UpLo

Definition at line 65 of file LLT.h.

         {
      PacketSize = internal::packet_traits<Scalar>::size,
      AlignmentMask = int(PacketSize)-1,
      UpLo = _UpLo
    };

Constructor & Destructor Documentation

template<typename _MatrixType, int _UpLo>

Eigen::LLT< _MatrixType, _UpLo >::LLT ( ) [inline]

Default Constructor.

The default constructor is useful in cases in which the user intends to perform decompositions via LLT::compute(const MatrixType&).

Definition at line 79 of file LLT.h.

: m_matrix(), m_isInitialized(false) {}

template<typename _MatrixType, int _UpLo>

Eigen::LLT< _MatrixType, _UpLo >::LLT ( Index size ) [inline, explicit]

Default Constructor with memory preallocation.

Like the default constructor but with preallocation of the internal data according to the specified problem size.

See also:: LLT()

Definition at line 87 of file LLT.h.

                             : m_matrix(size, size),
                    m_isInitialized(false) {}

template<typename _MatrixType, int _UpLo>

template<typename InputType >

Eigen::LLT< _MatrixType, _UpLo >::LLT ( const EigenBase< InputType > & matrix ) [inline, explicit]

Definition at line 91 of file LLT.h.

      : m_matrix(matrix.rows(), matrix.cols()),
        m_isInitialized(false)
    {
      compute(matrix.derived());
    }

Member Function Documentation

template<typename _MatrixType , int _UpLo>

template<typename RhsType , typename DstType >

void Eigen::LLT< _MatrixType, _UpLo >::_solve_impl	(	const RhsType &	rhs,
		DstType &	dst
	)		const

Definition at line 426 of file LLT.h.

{
  dst = rhs;
  solveInPlace(dst);
}

template<typename _MatrixType, int _UpLo>

static void Eigen::LLT< _MatrixType, _UpLo >::check_template_parameters ( ) [inline, static, protected]

Definition at line 176 of file LLT.h.

    {
      EIGEN_STATIC_ASSERT_NON_INTEGER(Scalar);
    }

template<typename _MatrixType, int _UpLo>

Index Eigen::LLT< _MatrixType, _UpLo >::cols ( ) const [inline]

Definition at line 163 of file LLT.h.

{ return m_matrix.cols(); }

template<typename MatrixType , int _UpLo>

template<typename InputType >

LLT< MatrixType, _UpLo > & Eigen::LLT< MatrixType, _UpLo >::compute ( const EigenBase< InputType > & a )

Computes / recomputes the Cholesky decomposition A = LL^* = U^*U of matrix

Returns:: a reference to *this

Example:

Output:

Definition at line 387 of file LLT.h.

{
  check_template_parameters();
  
  eigen_assert(a.rows()==a.cols());
  const Index size = a.rows();
  m_matrix.resize(size, size);
  m_matrix = a.derived();

  m_isInitialized = true;
  bool ok = Traits::inplace_decomposition(m_matrix);
  m_info = ok ? Success : NumericalIssue;

  return *this;
}

template<typename _MatrixType, int _UpLo>

ComputationInfo Eigen::LLT< _MatrixType, _UpLo >::info ( ) const [inline]

Reports whether previous computation was successful.

Returns:: Success if computation was succesful, NumericalIssue if the matrix.appears to be negative.

Definition at line 156 of file LLT.h.

    {
      eigen_assert(m_isInitialized && "LLT is not initialized.");
      return m_info;
    }

template<typename _MatrixType, int _UpLo>

Traits::MatrixL Eigen::LLT< _MatrixType, _UpLo >::matrixL ( ) const [inline]

Returns:: a view of the lower triangular matrix L

Definition at line 106 of file LLT.h.

    {
      eigen_assert(m_isInitialized && "LLT is not initialized.");
      return Traits::getL(m_matrix);
    }

template<typename _MatrixType, int _UpLo>

const MatrixType& Eigen::LLT< _MatrixType, _UpLo >::matrixLLT ( ) const [inline]

Returns:: the LLT decomposition matrix

TODO: document the storage layout

Definition at line 142 of file LLT.h.

    {
      eigen_assert(m_isInitialized && "LLT is not initialized.");
      return m_matrix;
    }

template<typename _MatrixType, int _UpLo>

Traits::MatrixU Eigen::LLT< _MatrixType, _UpLo >::matrixU ( ) const [inline]

Returns:: a view of the upper triangular matrix U

Definition at line 99 of file LLT.h.

    {
      eigen_assert(m_isInitialized && "LLT is not initialized.");
      return Traits::getU(m_matrix);
    }

template<typename _MatrixType , int _UpLo>

template<typename VectorType >

LLT< _MatrixType, _UpLo > Eigen::LLT< _MatrixType, _UpLo >::rankUpdate	(	const VectorType &	v,
		const RealScalar &	sigma = `1`
	)

Performs a rank one update (or dowdate) of the current decomposition. If A = LL^* before the rank one update, then after it we have LL^* = A + sigma * v v^* where v must be a vector of same dimension.

Definition at line 410 of file LLT.h.

{
  EIGEN_STATIC_ASSERT_VECTOR_ONLY(VectorType);
  eigen_assert(v.size()==m_matrix.cols());
  eigen_assert(m_isInitialized);
  if(internal::llt_inplace<typename MatrixType::Scalar, UpLo>::rankUpdate(m_matrix,v,sigma)>=0)
    m_info = NumericalIssue;
  else
    m_info = Success;

  return *this;
}

template<typename MatrixType , int _UpLo>

MatrixType Eigen::LLT< MatrixType, _UpLo >::reconstructedMatrix ( ) const

Returns:: the matrix represented by the decomposition, i.e., it returns the product: L L^*. This function is provided for debug purpose.

Definition at line 457 of file LLT.h.

{
  eigen_assert(m_isInitialized && "LLT is not initialized.");
  return matrixL() * matrixL().adjoint().toDenseMatrix();
}

template<typename _MatrixType, int _UpLo>

Index Eigen::LLT< _MatrixType, _UpLo >::rows ( ) const [inline]

Definition at line 162 of file LLT.h.

{ return m_matrix.rows(); }

template<typename _MatrixType, int _UpLo>

template<typename Rhs >

const Solve<LLT, Rhs> Eigen::LLT< _MatrixType, _UpLo >::solve ( const MatrixBase< Rhs > & b ) const [inline]

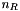Returns:: the solution x of using the current decomposition of A.

Since this LLT class assumes anyway that the matrix A is invertible, the solution theoretically exists and is unique regardless of b.

Example:

Output:

See also:: solveInPlace(), MatrixBase::llt(), SelfAdjointView::llt()

Definition at line 124 of file LLT.h.

    {
      eigen_assert(m_isInitialized && "LLT is not initialized.");
      eigen_assert(m_matrix.rows()==b.rows()
                && "LLT::solve(): invalid number of rows of the right hand side matrix b");
      return Solve<LLT, Rhs>(*this, b.derived());
    }

template<typename MatrixType , int _UpLo>

template<typename Derived >

void Eigen::LLT< MatrixType, _UpLo >::solveInPlace ( MatrixBase< Derived > & bAndX ) const

use x = llt_object.solve(x);

This is the in-place version of solve().

Parameters:

bAndX represents both the right-hand side matrix b and result x.

This version avoids a copy when the right hand side matrix b is not needed anymore.

See also:: LLT::solve(), MatrixBase::llt()

Definition at line 445 of file LLT.h.

{
  eigen_assert(m_isInitialized && "LLT is not initialized.");
  eigen_assert(m_matrix.rows()==bAndX.rows());
  matrixL().solveInPlace(bAndX);
  matrixU().solveInPlace(bAndX);
}

Member Data Documentation

template<typename _MatrixType, int _UpLo>

ComputationInfo Eigen::LLT< _MatrixType, _UpLo >::m_info [protected]

Definition at line 187 of file LLT.h.

template<typename _MatrixType, int _UpLo>

bool Eigen::LLT< _MatrixType, _UpLo >::m_isInitialized [protected]

Definition at line 186 of file LLT.h.

template<typename _MatrixType, int _UpLo>

MatrixType Eigen::LLT< _MatrixType, _UpLo >::m_matrix [protected]

Used to compute and store L The strict upper part is not used and even not initialized.

Definition at line 185 of file LLT.h.

The documentation for this class was generated from the following file:

LLT.h

Public Types

Public Member Functions

Static Protected Member Functions

Protected Attributes

Detailed Description

template<typename _MatrixType, int _UpLo> class Eigen::LLT< _MatrixType, _UpLo >

Member Typedef Documentation

Member Enumeration Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<typename _MatrixType, int _UpLo>
class Eigen::LLT< _MatrixType, _UpLo >