Expression of a selfadjoint matrix from a triangular part of a dense matrix. More...

#include <SelfAdjointView.h>

Inheritance diagram for Eigen::SelfAdjointView< _MatrixType, UpLo >:

Collaboration diagram for Eigen::SelfAdjointView< _MatrixType, UpLo >:

Public Types
enum	{ Mode = internal::traits<SelfAdjointView>::Mode, Flags = internal::traits<SelfAdjointView>::Flags }
typedef _MatrixType	MatrixType
typedef TriangularBase < SelfAdjointView >	Base
typedef internal::traits < SelfAdjointView > ::MatrixTypeNested	MatrixTypeNested
typedef internal::traits < SelfAdjointView > ::MatrixTypeNestedCleaned	MatrixTypeNestedCleaned
typedef internal::traits < SelfAdjointView >::Scalar	Scalar
	The type of coefficients in this matrix.
typedef MatrixType::StorageIndex	StorageIndex
typedef MatrixType::PlainObject	PlainObject
typedef NumTraits< Scalar >::Real	RealScalar
typedef Matrix< RealScalar, internal::traits< MatrixType > ::ColsAtCompileTime, 1 >	EigenvaluesReturnType
Public Member Functions
EIGEN_DEVICE_FUNC	SelfAdjointView (MatrixType &matrix)
EIGEN_DEVICE_FUNC Index	rows () const
EIGEN_DEVICE_FUNC Index	cols () const
EIGEN_DEVICE_FUNC Index	outerStride () const
EIGEN_DEVICE_FUNC Index	innerStride () const
EIGEN_DEVICE_FUNC Scalar	coeff (Index row, Index col) const
EIGEN_DEVICE_FUNC Scalar &	coeffRef (Index row, Index col)
EIGEN_DEVICE_FUNC const MatrixTypeNestedCleaned &	_expression () const
EIGEN_DEVICE_FUNC const MatrixTypeNestedCleaned &	nestedExpression () const
EIGEN_DEVICE_FUNC MatrixTypeNestedCleaned &	nestedExpression ()
template<typename OtherDerived >
EIGEN_DEVICE_FUNC const Product< SelfAdjointView, OtherDerived >	operator* (const MatrixBase< OtherDerived > &rhs) const
template<typename DerivedU , typename DerivedV >
EIGEN_DEVICE_FUNC SelfAdjointView &	rankUpdate (const MatrixBase< DerivedU > &u, const MatrixBase< DerivedV > &v, const Scalar &alpha=Scalar(1))
template<typename DerivedU >
EIGEN_DEVICE_FUNC SelfAdjointView &	rankUpdate (const MatrixBase< DerivedU > &u, const Scalar &alpha=Scalar(1))
const LLT< PlainObject, UpLo >	llt () const
const LDLT< PlainObject, UpLo >	ldlt () const
EIGEN_DEVICE_FUNC EigenvaluesReturnType	eigenvalues () const
	Computes the eigenvalues of a matrix.
EIGEN_DEVICE_FUNC RealScalar	operatorNorm () const
	Computes the L2 operator norm.
Protected Attributes
MatrixTypeNested	m_matrix
Friends
template<typename OtherDerived >
EIGEN_DEVICE_FUNC const Product< OtherDerived, SelfAdjointView >	operator* (const MatrixBase< OtherDerived > &lhs, const SelfAdjointView &rhs)
EIGEN_DEVICE_FUNC const SelfAdjointView< const CwiseUnaryOp < internal::scalar_multiple_op < Scalar >, MatrixType >, UpLo >	operator* (const Scalar &s, const SelfAdjointView &mat)

Detailed Description

template<typename _MatrixType, unsigned int UpLo>
class Eigen::SelfAdjointView< _MatrixType, UpLo >

Expression of a selfadjoint matrix from a triangular part of a dense matrix.

Parameters:

MatrixType	the type of the dense matrix storing the coefficients
TriangularPart	can be either `Lower` or `Upper`

This class is an expression of a sefladjoint matrix from a triangular part of a matrix with given dense storage of the coefficients. It is the return type of MatrixBase::selfadjointView() and most of the time this is the only way that it is used.

See also:: class TriangularBase, MatrixBase::selfadjointView()

Definition at line 49 of file SelfAdjointView.h.

Member Typedef Documentation

template<typename _MatrixType, unsigned int UpLo>

typedef TriangularBase<SelfAdjointView> Eigen::SelfAdjointView< _MatrixType, UpLo >::Base

Definition at line 55 of file SelfAdjointView.h.

template<typename _MatrixType, unsigned int UpLo>

typedef Matrix<RealScalar, internal::traits<MatrixType>::ColsAtCompileTime, 1> Eigen::SelfAdjointView< _MatrixType, UpLo >::EigenvaluesReturnType

Return type of eigenvalues()

Definition at line 175 of file SelfAdjointView.h.

template<typename _MatrixType, unsigned int UpLo>

typedef _MatrixType Eigen::SelfAdjointView< _MatrixType, UpLo >::MatrixType

Definition at line 54 of file SelfAdjointView.h.

template<typename _MatrixType, unsigned int UpLo>

typedef internal::traits<SelfAdjointView>::MatrixTypeNested Eigen::SelfAdjointView< _MatrixType, UpLo >::MatrixTypeNested

Definition at line 56 of file SelfAdjointView.h.

template<typename _MatrixType, unsigned int UpLo>

typedef internal::traits<SelfAdjointView>::MatrixTypeNestedCleaned Eigen::SelfAdjointView< _MatrixType, UpLo >::MatrixTypeNestedCleaned

Definition at line 57 of file SelfAdjointView.h.

template<typename _MatrixType, unsigned int UpLo>

typedef MatrixType::PlainObject Eigen::SelfAdjointView< _MatrixType, UpLo >::PlainObject

Definition at line 67 of file SelfAdjointView.h.

template<typename _MatrixType, unsigned int UpLo>

typedef NumTraits<Scalar>::Real Eigen::SelfAdjointView< _MatrixType, UpLo >::RealScalar

Real part of Scalar

Definition at line 173 of file SelfAdjointView.h.

template<typename _MatrixType, unsigned int UpLo>

typedef internal::traits<SelfAdjointView>::Scalar Eigen::SelfAdjointView< _MatrixType, UpLo >::Scalar

The type of coefficients in this matrix.

Reimplemented from Eigen::TriangularBase< SelfAdjointView< _MatrixType, UpLo > >.

Definition at line 60 of file SelfAdjointView.h.

template<typename _MatrixType, unsigned int UpLo>

typedef MatrixType::StorageIndex Eigen::SelfAdjointView< _MatrixType, UpLo >::StorageIndex

Reimplemented from Eigen::TriangularBase< SelfAdjointView< _MatrixType, UpLo > >.

Definition at line 61 of file SelfAdjointView.h.

Member Enumeration Documentation

template<typename _MatrixType, unsigned int UpLo>

anonymous enum

Enumerator:

Mode
Flags

Definition at line 63 of file SelfAdjointView.h.

         {
      Mode = internal::traits<SelfAdjointView>::Mode,
      Flags = internal::traits<SelfAdjointView>::Flags
    };

Constructor & Destructor Documentation

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC Eigen::SelfAdjointView< _MatrixType, UpLo >::SelfAdjointView ( MatrixType & matrix ) [inline, explicit]

Definition at line 70 of file SelfAdjointView.h.

                                                        : m_matrix(matrix)
    {}

Member Function Documentation

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC const MatrixTypeNestedCleaned& Eigen::SelfAdjointView< _MatrixType, UpLo >::_expression ( ) const [inline]

Definition at line 105 of file SelfAdjointView.h.

{ return m_matrix; }

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC Scalar Eigen::SelfAdjointView< _MatrixType, UpLo >::coeff	(	Index	row,
		Index	col
	)		const `[inline]`

See also:: MatrixBase::coeff()

Warning:: the coordinates must fit into the referenced triangular part

Reimplemented from Eigen::TriangularBase< SelfAdjointView< _MatrixType, UpLo > >.

Definition at line 86 of file SelfAdjointView.h.

    {
      Base::check_coordinates_internal(row, col);
      return m_matrix.coeff(row, col);
    }

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC Scalar& Eigen::SelfAdjointView< _MatrixType, UpLo >::coeffRef	(	Index	row,
		Index	col
	)		`[inline]`

See also:: MatrixBase::coeffRef()

Warning:: the coordinates must fit into the referenced triangular part

Reimplemented from Eigen::TriangularBase< SelfAdjointView< _MatrixType, UpLo > >.

Definition at line 96 of file SelfAdjointView.h.

    {
      EIGEN_STATIC_ASSERT_LVALUE(SelfAdjointView);
      Base::check_coordinates_internal(row, col);
      return m_matrix.coeffRef(row, col);
    }

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC Index Eigen::SelfAdjointView< _MatrixType, UpLo >::cols ( void ) const [inline]

Returns:: the number of columns.

See also:: rows(), ColsAtCompileTime

Reimplemented from Eigen::TriangularBase< SelfAdjointView< _MatrixType, UpLo > >.

Definition at line 76 of file SelfAdjointView.h.

{ return m_matrix.cols(); }

template<typename MatrixType , unsigned int UpLo>

SelfAdjointView< MatrixType, UpLo >::EigenvaluesReturnType Eigen::SelfAdjointView< MatrixType, UpLo >::eigenvalues ( ) const [inline]

Computes the eigenvalues of a matrix.

Returns:: Column vector containing the eigenvalues.

This function computes the eigenvalues with the help of the SelfAdjointEigenSolver class. The eigenvalues are repeated according to their algebraic multiplicity, so there are as many eigenvalues as rows in the matrix.

Example:

Output:

See also:: SelfAdjointEigenSolver::eigenvalues(), MatrixBase::eigenvalues()

Definition at line 89 of file MatrixBaseEigenvalues.h.

{
  typedef typename SelfAdjointView<MatrixType, UpLo>::PlainObject PlainObject;
  PlainObject thisAsMatrix(*this);
  return SelfAdjointEigenSolver<PlainObject>(thisAsMatrix, false).eigenvalues();
}

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC Index Eigen::SelfAdjointView< _MatrixType, UpLo >::innerStride ( ) const [inline]

Reimplemented from Eigen::TriangularBase< SelfAdjointView< _MatrixType, UpLo > >.

Definition at line 80 of file SelfAdjointView.h.

{ return m_matrix.innerStride(); }

template<typename MatrixType , unsigned int UpLo>

const LDLT< typename SelfAdjointView< MatrixType, UpLo >::PlainObject, UpLo > Eigen::SelfAdjointView< MatrixType, UpLo >::ldlt ( ) const [inline]

Returns:: the Cholesky decomposition with full pivoting without square root of *this

See also:: MatrixBase::ldlt()

Definition at line 582 of file LDLT.h.

{
  return LDLT<PlainObject,UpLo>(m_matrix);
}

template<typename MatrixType , unsigned int UpLo>

const LLT< typename SelfAdjointView< MatrixType, UpLo >::PlainObject, UpLo > Eigen::SelfAdjointView< MatrixType, UpLo >::llt ( ) const [inline]

Returns:: the LLT decomposition of *this

See also:: SelfAdjointView::llt()

Definition at line 481 of file LLT.h.

{
  return LLT<PlainObject,UpLo>(m_matrix);
}

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC const MatrixTypeNestedCleaned& Eigen::SelfAdjointView< _MatrixType, UpLo >::nestedExpression ( ) const [inline]

Definition at line 108 of file SelfAdjointView.h.

{ return m_matrix; }

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC MatrixTypeNestedCleaned& Eigen::SelfAdjointView< _MatrixType, UpLo >::nestedExpression ( ) [inline]

Definition at line 110 of file SelfAdjointView.h.

{ return m_matrix; }

template<typename _MatrixType, unsigned int UpLo>

template<typename OtherDerived >

EIGEN_DEVICE_FUNC const Product<SelfAdjointView,OtherDerived> Eigen::SelfAdjointView< _MatrixType, UpLo >::operator* ( const MatrixBase< OtherDerived > & rhs ) const [inline]

Efficient triangular matrix times vector/matrix product

Definition at line 116 of file SelfAdjointView.h.

    {
      return Product<SelfAdjointView,OtherDerived>(*this, rhs.derived());
    }

template<typename MatrixType , unsigned int UpLo>

SelfAdjointView< MatrixType, UpLo >::RealScalar Eigen::SelfAdjointView< MatrixType, UpLo >::operatorNorm ( ) const [inline]

Computes the L2 operator norm.

Returns:: Operator norm of the matrix.

This function computes the L2 operator norm of a self-adjoint matrix. For a self-adjoint matrix, the operator norm is the largest eigenvalue.

The current implementation uses the eigenvalues of the matrix, as computed by eigenvalues(), to compute the operator norm of the matrix.

Example:

Output:

See also:: eigenvalues(), MatrixBase::operatorNorm()

Definition at line 153 of file MatrixBaseEigenvalues.h.

{
  return eigenvalues().cwiseAbs().maxCoeff();
}

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC Index Eigen::SelfAdjointView< _MatrixType, UpLo >::outerStride ( ) const [inline]

Reimplemented from Eigen::TriangularBase< SelfAdjointView< _MatrixType, UpLo > >.

Definition at line 78 of file SelfAdjointView.h.

{ return m_matrix.outerStride(); }

template<typename MatrixType , unsigned int UpLo>

template<typename DerivedU , typename DerivedV >

SelfAdjointView< MatrixType, UpLo > & Eigen::SelfAdjointView< MatrixType, UpLo >::rankUpdate	(	const MatrixBase< DerivedU > &	u,
		const MatrixBase< DerivedV > &	v,
		const Scalar &	alpha = `Scalar(1)`
	)

Perform a symmetric rank 2 update of the selfadjoint matrix *this: 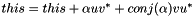$this = this + \alpha u v^* + conj(\alpha) v u^*$

Returns:: a reference to *this

The vectors u and v must be column vectors, however they can be a adjoint expression without any overhead. Only the meaningful triangular part of the matrix is updated, the rest is left unchanged.

See also:: rankUpdate(const MatrixBase<DerivedU>&, Scalar)

Definition at line 61 of file SelfadjointRank2Update.h.

{
  typedef internal::blas_traits<DerivedU> UBlasTraits;
  typedef typename UBlasTraits::DirectLinearAccessType ActualUType;
  typedef typename internal::remove_all<ActualUType>::type _ActualUType;
  typename internal::add_const_on_value_type<ActualUType>::type actualU = UBlasTraits::extract(u.derived());

  typedef internal::blas_traits<DerivedV> VBlasTraits;
  typedef typename VBlasTraits::DirectLinearAccessType ActualVType;
  typedef typename internal::remove_all<ActualVType>::type _ActualVType;
  typename internal::add_const_on_value_type<ActualVType>::type actualV = VBlasTraits::extract(v.derived());

  // If MatrixType is row major, then we use the routine for lower triangular in the upper triangular case and
  // vice versa, and take the complex conjugate of all coefficients and vector entries.

  enum { IsRowMajor = (internal::traits<MatrixType>::Flags&RowMajorBit) ? 1 : 0 };
  Scalar actualAlpha = alpha * UBlasTraits::extractScalarFactor(u.derived())
                             * numext::conj(VBlasTraits::extractScalarFactor(v.derived()));
  if (IsRowMajor)
    actualAlpha = numext::conj(actualAlpha);

  typedef typename internal::remove_all<typename internal::conj_expr_if<IsRowMajor ^ UBlasTraits::NeedToConjugate,_ActualUType>::type>::type UType;
  typedef typename internal::remove_all<typename internal::conj_expr_if<IsRowMajor ^ VBlasTraits::NeedToConjugate,_ActualVType>::type>::type VType;
  internal::selfadjoint_rank2_update_selector<Scalar, Index, UType, VType,
    (IsRowMajor ? int(UpLo==Upper ? Lower : Upper) : UpLo)>
    ::run(_expression().const_cast_derived().data(),_expression().outerStride(),UType(actualU),VType(actualV),actualAlpha);

  return *this;
}

template<typename MatrixType , unsigned int UpLo>

template<typename DerivedU >

SelfAdjointView< MatrixType, UpLo > & Eigen::SelfAdjointView< MatrixType, UpLo >::rankUpdate	(	const MatrixBase< DerivedU > &	u,
		const Scalar &	alpha = `Scalar(1)`
	)

Perform a symmetric rank K update of the selfadjoint matrix *this: 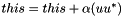$this = this + \alpha ( u u^* )$ where u is a vector or matrix.

Returns:: a reference to *this

Note that to perform 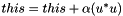$this = this + \alpha ( u^* u )$ you can simply call this function with u.adjoint().

See also:: rankUpdate(const MatrixBase<DerivedU>&, const MatrixBase<DerivedV>&, Scalar)

Definition at line 124 of file SelfadjointProduct.h.

{
  selfadjoint_product_selector<MatrixType,DerivedU,UpLo>::run(_expression().const_cast_derived(), u.derived(), alpha);

  return *this;
}

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC Index Eigen::SelfAdjointView< _MatrixType, UpLo >::rows ( void ) const [inline]

Returns:: the number of rows.

See also:: cols(), RowsAtCompileTime

Reimplemented from Eigen::TriangularBase< SelfAdjointView< _MatrixType, UpLo > >.

Definition at line 74 of file SelfAdjointView.h.

{ return m_matrix.rows(); }

Friends And Related Function Documentation

template<typename _MatrixType, unsigned int UpLo>

template<typename OtherDerived >

EIGEN_DEVICE_FUNC const Product<OtherDerived,SelfAdjointView> operator*	(	const MatrixBase< OtherDerived > &	lhs,
		const SelfAdjointView< _MatrixType, UpLo > &	rhs
	)		`[friend]`

Efficient vector/matrix times triangular matrix product

Definition at line 125 of file SelfAdjointView.h.

    {
      return Product<OtherDerived,SelfAdjointView>(lhs.derived(),rhs);
    }

template<typename _MatrixType, unsigned int UpLo>

EIGEN_DEVICE_FUNC const SelfAdjointView<const CwiseUnaryOp<internal::scalar_multiple_op<Scalar>,MatrixType>,UpLo> operator*	(	const Scalar &	s,
		const SelfAdjointView< _MatrixType, UpLo > &	mat
	)		`[friend]`

Definition at line 132 of file SelfAdjointView.h.

    {
      return (s*mat.nestedExpression()).template selfadjointView<UpLo>();
    }

Member Data Documentation

template<typename _MatrixType, unsigned int UpLo>

MatrixTypeNested Eigen::SelfAdjointView< _MatrixType, UpLo >::m_matrix [protected]

Definition at line 183 of file SelfAdjointView.h.

The documentation for this class was generated from the following files:

Public Types

Public Member Functions

Protected Attributes

Friends

Detailed Description

template<typename _MatrixType, unsigned int UpLo> class Eigen::SelfAdjointView< _MatrixType, UpLo >

Member Typedef Documentation

Member Enumeration Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Member Data Documentation

template<typename _MatrixType, unsigned int UpLo>
class Eigen::SelfAdjointView< _MatrixType, UpLo >