|
MOAB
4.9.3pre
|
|
MOAB
4.9.3pre
|
Base class of SVD algorithms. More...
#include <SVDBase.h>
Public Types | |
| enum | { RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, DiagSizeAtCompileTime = EIGEN_SIZE_MIN_PREFER_DYNAMIC(RowsAtCompileTime,ColsAtCompileTime), MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime, MaxDiagSizeAtCompileTime = EIGEN_SIZE_MIN_PREFER_FIXED(MaxRowsAtCompileTime,MaxColsAtCompileTime), MatrixOptions = MatrixType::Options } |
| typedef internal::traits < Derived >::MatrixType | MatrixType |
| typedef MatrixType::Scalar | Scalar |
| typedef NumTraits< typename MatrixType::Scalar >::Real | RealScalar |
| typedef MatrixType::StorageIndex | StorageIndex |
| typedef Eigen::Index | Index |
| typedef Matrix< Scalar, RowsAtCompileTime, RowsAtCompileTime, MatrixOptions, MaxRowsAtCompileTime, MaxRowsAtCompileTime > | MatrixUType |
| typedef Matrix< Scalar, ColsAtCompileTime, ColsAtCompileTime, MatrixOptions, MaxColsAtCompileTime, MaxColsAtCompileTime > | MatrixVType |
| typedef internal::plain_diag_type < MatrixType, RealScalar > ::type | SingularValuesType |
Public Member Functions | |
| Derived & | derived () |
| const Derived & | derived () const |
| const MatrixUType & | matrixU () const |
| const MatrixVType & | matrixV () const |
| const SingularValuesType & | singularValues () const |
| Index | nonzeroSingularValues () const |
| Index | rank () const |
| Derived & | setThreshold (const RealScalar &threshold) |
| Derived & | setThreshold (Default_t) |
| RealScalar | threshold () const |
| bool | computeU () const |
| bool | computeV () const |
| Index | rows () const |
| Index | cols () const |
| template<typename Rhs > | |
| const Solve< Derived, Rhs > | solve (const MatrixBase< Rhs > &b) const |
| template<typename RhsType , typename DstType > | |
| EIGEN_DEVICE_FUNC void | _solve_impl (const RhsType &rhs, DstType &dst) const |
Protected Member Functions | |
| bool | allocate (Index rows, Index cols, unsigned int computationOptions) |
| SVDBase () | |
| Default Constructor. | |
Static Protected Member Functions | |
| static void | check_template_parameters () |
Protected Attributes | |
| MatrixUType | m_matrixU |
| MatrixVType | m_matrixV |
| SingularValuesType | m_singularValues |
| bool | m_isInitialized |
| bool | m_isAllocated |
| bool | m_usePrescribedThreshold |
| bool | m_computeFullU |
| bool | m_computeThinU |
| bool | m_computeFullV |
| bool | m_computeThinV |
| unsigned int | m_computationOptions |
| Index | m_nonzeroSingularValues |
| Index | m_rows |
| Index | m_cols |
| Index | m_diagSize |
| RealScalar | m_prescribedThreshold |
Base class of SVD algorithms.
| Derived | the type of the actual SVD decomposition |
SVD decomposition consists in decomposing any n-by-p matrix A as a product
![\[ A = U S V^* \]](form_180.png)
where U is a n-by-n unitary, V is a p-by-p unitary, and S is a n-by-p real positive matrix which is zero outside of its main diagonal; the diagonal entries of S are known as the singular values of A and the columns of U and V are known as the left and right singular vectors of A respectively.
Singular values are always sorted in decreasing order.
You can ask for only thin U or V to be computed, meaning the following. In case of a rectangular n-by-p matrix, letting m be the smaller value among n and p, there are only m singular vectors; the remaining columns of U and V do not correspond to actual singular vectors. Asking for thin U or V means asking for only their m first columns to be formed. So U is then a n-by-m matrix, and V is then a p-by-m matrix. Notice that thin U and V are all you need for (least squares) solving.
If the input matrix has inf or nan coefficients, the result of the computation is undefined, but the computation is guaranteed to terminate in finite (and reasonable) time.
| typedef Eigen::Index Eigen::SVDBase< Derived >::Index |
| typedef internal::traits<Derived>::MatrixType Eigen::SVDBase< Derived >::MatrixType |
Reimplemented in Eigen::JacobiSVD< _MatrixType, QRPreconditioner >, and Eigen::BDCSVD< _MatrixType >.
| typedef Matrix<Scalar, RowsAtCompileTime, RowsAtCompileTime, MatrixOptions, MaxRowsAtCompileTime, MaxRowsAtCompileTime> Eigen::SVDBase< Derived >::MatrixUType |
Reimplemented in Eigen::JacobiSVD< _MatrixType, QRPreconditioner >, and Eigen::BDCSVD< _MatrixType >.
| typedef Matrix<Scalar, ColsAtCompileTime, ColsAtCompileTime, MatrixOptions, MaxColsAtCompileTime, MaxColsAtCompileTime> Eigen::SVDBase< Derived >::MatrixVType |
Reimplemented in Eigen::JacobiSVD< _MatrixType, QRPreconditioner >, and Eigen::BDCSVD< _MatrixType >.
| typedef NumTraits<typename MatrixType::Scalar>::Real Eigen::SVDBase< Derived >::RealScalar |
Reimplemented in Eigen::JacobiSVD< _MatrixType, QRPreconditioner >, and Eigen::BDCSVD< _MatrixType >.
| typedef MatrixType::Scalar Eigen::SVDBase< Derived >::Scalar |
Reimplemented in Eigen::JacobiSVD< _MatrixType, QRPreconditioner >, and Eigen::BDCSVD< _MatrixType >.
| typedef internal::plain_diag_type<MatrixType, RealScalar>::type Eigen::SVDBase< Derived >::SingularValuesType |
Reimplemented in Eigen::JacobiSVD< _MatrixType, QRPreconditioner >, and Eigen::BDCSVD< _MatrixType >.
| typedef MatrixType::StorageIndex Eigen::SVDBase< Derived >::StorageIndex |
| anonymous enum |
| RowsAtCompileTime | |
| ColsAtCompileTime | |
| DiagSizeAtCompileTime | |
| MaxRowsAtCompileTime | |
| MaxColsAtCompileTime | |
| MaxDiagSizeAtCompileTime | |
| MatrixOptions |
Definition at line 57 of file SVDBase.h.
{
RowsAtCompileTime = MatrixType::RowsAtCompileTime,
ColsAtCompileTime = MatrixType::ColsAtCompileTime,
DiagSizeAtCompileTime = EIGEN_SIZE_MIN_PREFER_DYNAMIC(RowsAtCompileTime,ColsAtCompileTime),
MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime,
MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime,
MaxDiagSizeAtCompileTime = EIGEN_SIZE_MIN_PREFER_FIXED(MaxRowsAtCompileTime,MaxColsAtCompileTime),
MatrixOptions = MatrixType::Options
};
| Eigen::SVDBase< Derived >::SVDBase | ( | ) | [inline, protected] |
Default Constructor.
Default constructor of SVDBase
Definition at line 244 of file SVDBase.h.
: m_isInitialized(false), m_isAllocated(false), m_usePrescribedThreshold(false), m_computationOptions(0), m_rows(-1), m_cols(-1), m_diagSize(0) { check_template_parameters(); }
| void Eigen::SVDBase< Derived >::_solve_impl | ( | const RhsType & | rhs, |
| DstType & | dst | ||
| ) | const |
Definition at line 260 of file SVDBase.h.
{
eigen_assert(rhs.rows() == rows());
// A = U S V^*
// So A^{-1} = V S^{-1} U^*
Matrix<Scalar, Dynamic, RhsType::ColsAtCompileTime, 0, MatrixType::MaxRowsAtCompileTime, RhsType::MaxColsAtCompileTime> tmp;
Index l_rank = rank();
tmp.noalias() = m_matrixU.leftCols(l_rank).adjoint() * rhs;
tmp = m_singularValues.head(l_rank).asDiagonal().inverse() * tmp;
dst = m_matrixV.leftCols(l_rank) * tmp;
}
| bool Eigen::SVDBase< MatrixType >::allocate | ( | Index | rows, |
| Index | cols, | ||
| unsigned int | computationOptions | ||
| ) | [protected] |
Reimplemented in Eigen::JacobiSVD< _MatrixType, QRPreconditioner >, and Eigen::BDCSVD< _MatrixType >.
Definition at line 276 of file SVDBase.h.
{
eigen_assert(rows >= 0 && cols >= 0);
if (m_isAllocated &&
rows == m_rows &&
cols == m_cols &&
computationOptions == m_computationOptions)
{
return true;
}
m_rows = rows;
m_cols = cols;
m_isInitialized = false;
m_isAllocated = true;
m_computationOptions = computationOptions;
m_computeFullU = (computationOptions & ComputeFullU) != 0;
m_computeThinU = (computationOptions & ComputeThinU) != 0;
m_computeFullV = (computationOptions & ComputeFullV) != 0;
m_computeThinV = (computationOptions & ComputeThinV) != 0;
eigen_assert(!(m_computeFullU && m_computeThinU) && "SVDBase: you can't ask for both full and thin U");
eigen_assert(!(m_computeFullV && m_computeThinV) && "SVDBase: you can't ask for both full and thin V");
eigen_assert(EIGEN_IMPLIES(m_computeThinU || m_computeThinV, MatrixType::ColsAtCompileTime==Dynamic) &&
"SVDBase: thin U and V are only available when your matrix has a dynamic number of columns.");
m_diagSize = (std::min)(m_rows, m_cols);
m_singularValues.resize(m_diagSize);
if(RowsAtCompileTime==Dynamic)
m_matrixU.resize(m_rows, m_computeFullU ? m_rows : m_computeThinU ? m_diagSize : 0);
if(ColsAtCompileTime==Dynamic)
m_matrixV.resize(m_cols, m_computeFullV ? m_cols : m_computeThinV ? m_diagSize : 0);
return false;
}
| static void Eigen::SVDBase< Derived >::check_template_parameters | ( | ) | [inline, static, protected] |
| Index Eigen::SVDBase< Derived >::cols | ( | void | ) | const [inline] |
| bool Eigen::SVDBase< Derived >::computeU | ( | ) | const [inline] |
Definition at line 189 of file SVDBase.h.
{ return m_computeFullU || m_computeThinU; }
| bool Eigen::SVDBase< Derived >::computeV | ( | ) | const [inline] |
Definition at line 191 of file SVDBase.h.
{ return m_computeFullV || m_computeThinV; }
| Derived& Eigen::SVDBase< Derived >::derived | ( | ) | [inline] |
| const Derived& Eigen::SVDBase< Derived >::derived | ( | ) | const [inline] |
| const MatrixUType& Eigen::SVDBase< Derived >::matrixU | ( | ) | const [inline] |
For the SVD decomposition of a n-by-p matrix, letting m be the minimum of n and p, the U matrix is n-by-n if you asked for ComputeFullU , and is n-by-m if you asked for ComputeThinU .
The m first columns of U are the left singular vectors of the matrix being decomposed.
This method asserts that you asked for U to be computed.
Definition at line 83 of file SVDBase.h.
{
eigen_assert(m_isInitialized && "SVD is not initialized.");
eigen_assert(computeU() && "This SVD decomposition didn't compute U. Did you ask for it?");
return m_matrixU;
}
| const MatrixVType& Eigen::SVDBase< Derived >::matrixV | ( | ) | const [inline] |
For the SVD decomposition of a n-by-p matrix, letting m be the minimum of n and p, the V matrix is p-by-p if you asked for ComputeFullV , and is p-by-m if you asked for ComputeThinV .
The m first columns of V are the right singular vectors of the matrix being decomposed.
This method asserts that you asked for V to be computed.
Definition at line 99 of file SVDBase.h.
{
eigen_assert(m_isInitialized && "SVD is not initialized.");
eigen_assert(computeV() && "This SVD decomposition didn't compute V. Did you ask for it?");
return m_matrixV;
}
| Index Eigen::SVDBase< Derived >::nonzeroSingularValues | ( | ) | const [inline] |
Definition at line 118 of file SVDBase.h.
{
eigen_assert(m_isInitialized && "SVD is not initialized.");
return m_nonzeroSingularValues;
}
| Index Eigen::SVDBase< Derived >::rank | ( | ) | const [inline] |
*this is the SVD.Definition at line 130 of file SVDBase.h.
{
using std::abs;
using std::max;
eigen_assert(m_isInitialized && "JacobiSVD is not initialized.");
if(m_singularValues.size()==0) return 0;
RealScalar premultiplied_threshold = (max)(m_singularValues.coeff(0) * threshold(), (std::numeric_limits<RealScalar>::min)());
Index i = m_nonzeroSingularValues-1;
while(i>=0 && m_singularValues.coeff(i) < premultiplied_threshold) --i;
return i+1;
}
| Index Eigen::SVDBase< Derived >::rows | ( | void | ) | const [inline] |
| Derived& Eigen::SVDBase< Derived >::setThreshold | ( | const RealScalar & | threshold | ) | [inline] |
Allows to prescribe a threshold to be used by certain methods, such as rank() and solve(), which need to determine when singular values are to be considered nonzero. This is not used for the SVD decomposition itself.
When it needs to get the threshold value, Eigen calls threshold(). The default is NumTraits<Scalar>::epsilon()
| threshold | The new value to use as the threshold. |
A singular value will be considered nonzero if its value is strictly greater than 
.
If you want to come back to the default behavior, call setThreshold(Default_t)
Definition at line 156 of file SVDBase.h.
{
m_usePrescribedThreshold = true;
m_prescribedThreshold = threshold;
return derived();
}
| Derived& Eigen::SVDBase< Derived >::setThreshold | ( | Default_t | ) | [inline] |
Allows to come back to the default behavior, letting Eigen use its default formula for determining the threshold.
You should pass the special object Eigen::Default as parameter here.
svd.setThreshold(Eigen::Default);
See the documentation of setThreshold(const RealScalar&).
Definition at line 171 of file SVDBase.h.
{
m_usePrescribedThreshold = false;
return derived();
}
| const SingularValuesType& Eigen::SVDBase< Derived >::singularValues | ( | ) | const [inline] |
For the SVD decomposition of a n-by-p matrix, letting m be the minimum of n and p, the returned vector has size m. Singular values are always sorted in decreasing order.
Definition at line 111 of file SVDBase.h.
{
eigen_assert(m_isInitialized && "SVD is not initialized.");
return m_singularValues;
}
| const Solve<Derived, Rhs> Eigen::SVDBase< Derived >::solve | ( | const MatrixBase< Rhs > & | b | ) | const [inline] |
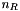using the current SVD decomposition of A.| b | the right-hand-side of the equation to solve. |
. Definition at line 207 of file SVDBase.h.
{
eigen_assert(m_isInitialized && "SVD is not initialized.");
eigen_assert(computeU() && computeV() && "SVD::solve() requires both unitaries U and V to be computed (thin unitaries suffice).");
return Solve<Derived, Rhs>(derived(), b.derived());
}
| RealScalar Eigen::SVDBase< Derived >::threshold | ( | ) | const [inline] |
Returns the threshold that will be used by certain methods such as rank().
See the documentation of setThreshold(const RealScalar&).
Definition at line 181 of file SVDBase.h.
{
eigen_assert(m_isInitialized || m_usePrescribedThreshold);
return m_usePrescribedThreshold ? m_prescribedThreshold
: (std::max<Index>)(1,m_diagSize)*NumTraits<Scalar>::epsilon();
}
Index Eigen::SVDBase< Derived >::m_cols [protected] |
unsigned int Eigen::SVDBase< Derived >::m_computationOptions [protected] |
bool Eigen::SVDBase< Derived >::m_computeFullU [protected] |
bool Eigen::SVDBase< Derived >::m_computeFullV [protected] |
bool Eigen::SVDBase< Derived >::m_computeThinU [protected] |
bool Eigen::SVDBase< Derived >::m_computeThinV [protected] |
Index Eigen::SVDBase< Derived >::m_diagSize [protected] |
bool Eigen::SVDBase< Derived >::m_isAllocated [protected] |
bool Eigen::SVDBase< Derived >::m_isInitialized [protected] |
MatrixUType Eigen::SVDBase< Derived >::m_matrixU [protected] |
MatrixVType Eigen::SVDBase< Derived >::m_matrixV [protected] |
Index Eigen::SVDBase< Derived >::m_nonzeroSingularValues [protected] |
RealScalar Eigen::SVDBase< Derived >::m_prescribedThreshold [protected] |
Index Eigen::SVDBase< Derived >::m_rows [protected] |
SingularValuesType Eigen::SVDBase< Derived >::m_singularValues [protected] |
bool Eigen::SVDBase< Derived >::m_usePrescribedThreshold [protected] |
1.7.6.1