|
MOAB
4.9.3pre
|
|
MOAB
4.9.3pre
|
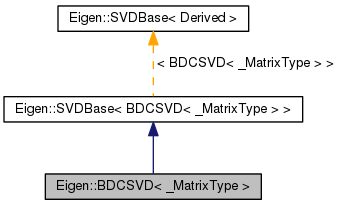
class Bidiagonal Divide and Conquer SVD More...
#include <BDCSVD.h>

Public Types | |
| enum | { RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, DiagSizeAtCompileTime = EIGEN_SIZE_MIN_PREFER_DYNAMIC(RowsAtCompileTime, ColsAtCompileTime), MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime, MaxDiagSizeAtCompileTime = EIGEN_SIZE_MIN_PREFER_FIXED(MaxRowsAtCompileTime, MaxColsAtCompileTime), MatrixOptions = MatrixType::Options } |
| typedef _MatrixType | MatrixType |
| typedef MatrixType::Scalar | Scalar |
| typedef NumTraits< typename MatrixType::Scalar >::Real | RealScalar |
| typedef Base::MatrixUType | MatrixUType |
| typedef Base::MatrixVType | MatrixVType |
| typedef Base::SingularValuesType | SingularValuesType |
| typedef Matrix< Scalar, Dynamic, Dynamic, ColMajor > | MatrixX |
| typedef Matrix< RealScalar, Dynamic, Dynamic, ColMajor > | MatrixXr |
| typedef Matrix< RealScalar, Dynamic, 1 > | VectorType |
| typedef Array< RealScalar, Dynamic, 1 > | ArrayXr |
| typedef Array< Index, 1, Dynamic > | ArrayXi |
| typedef Ref< ArrayXr > | ArrayRef |
| typedef Ref< ArrayXi > | IndicesRef |
Public Member Functions | |
| BDCSVD () | |
| Default Constructor. | |
| BDCSVD (Index p_rows, Index p_cols, unsigned int computationOptions=0) | |
| Default Constructor with memory preallocation. | |
| BDCSVD (const MatrixType &matrix, unsigned int computationOptions=0) | |
| Constructor performing the decomposition of given matrix. | |
| ~BDCSVD () | |
| BDCSVD & | compute (const MatrixType &matrix, unsigned int computationOptions) |
| Method performing the decomposition of given matrix using custom options. | |
| BDCSVD & | compute (const MatrixType &matrix) |
| Method performing the decomposition of given matrix using current options. | |
| void | setSwitchSize (int s) |
Public Attributes | |
| int | m_numIters |
Protected Attributes | |
| MatrixXr | m_naiveU |
| MatrixXr | m_naiveV |
| MatrixXr | m_computed |
| Index | m_nRec |
| ArrayXr | m_workspace |
| ArrayXi | m_workspaceI |
| int | m_algoswap |
| bool | m_isTranspose |
| bool | m_compU |
| bool | m_compV |
Private Types | |
| typedef SVDBase< BDCSVD > | Base |
Private Member Functions | |
| void | allocate (Index rows, Index cols, unsigned int computationOptions) |
| void | divide (Index firstCol, Index lastCol, Index firstRowW, Index firstColW, Index shift) |
| void | computeSVDofM (Index firstCol, Index n, MatrixXr &U, VectorType &singVals, MatrixXr &V) |
| void | computeSingVals (const ArrayRef &col0, const ArrayRef &diag, const IndicesRef &perm, VectorType &singVals, ArrayRef shifts, ArrayRef mus) |
| void | perturbCol0 (const ArrayRef &col0, const ArrayRef &diag, const IndicesRef &perm, const VectorType &singVals, const ArrayRef &shifts, const ArrayRef &mus, ArrayRef zhat) |
| void | computeSingVecs (const ArrayRef &zhat, const ArrayRef &diag, const IndicesRef &perm, const VectorType &singVals, const ArrayRef &shifts, const ArrayRef &mus, MatrixXr &U, MatrixXr &V) |
| void | deflation43 (Index firstCol, Index shift, Index i, Index size) |
| void | deflation44 (Index firstColu, Index firstColm, Index firstRowW, Index firstColW, Index i, Index j, Index size) |
| void | deflation (Index firstCol, Index lastCol, Index k, Index firstRowW, Index firstColW, Index shift) |
| template<typename HouseholderU , typename HouseholderV , typename NaiveU , typename NaiveV > | |
| void | copyUV (const HouseholderU &householderU, const HouseholderV &householderV, const NaiveU &naiveU, const NaiveV &naivev) |
| void | structured_update (Block< MatrixXr, Dynamic, Dynamic > A, const MatrixXr &B, Index n1) |
Static Private Member Functions | |
| static RealScalar | secularEq (RealScalar x, const ArrayRef &col0, const ArrayRef &diag, const IndicesRef &perm, const ArrayRef &diagShifted, RealScalar shift) |
class Bidiagonal Divide and Conquer SVD
| _MatrixType | the type of the matrix of which we are computing the SVD decomposition |
| typedef Ref<ArrayXr> Eigen::BDCSVD< _MatrixType >::ArrayRef |
| typedef Array<Index,1,Dynamic> Eigen::BDCSVD< _MatrixType >::ArrayXi |
| typedef Array<RealScalar, Dynamic, 1> Eigen::BDCSVD< _MatrixType >::ArrayXr |
typedef SVDBase<BDCSVD> Eigen::BDCSVD< _MatrixType >::Base [private] |
| typedef Ref<ArrayXi> Eigen::BDCSVD< _MatrixType >::IndicesRef |
| typedef _MatrixType Eigen::BDCSVD< _MatrixType >::MatrixType |
Reimplemented from Eigen::SVDBase< BDCSVD< _MatrixType > >.
| typedef Base::MatrixUType Eigen::BDCSVD< _MatrixType >::MatrixUType |
Reimplemented from Eigen::SVDBase< BDCSVD< _MatrixType > >.
| typedef Base::MatrixVType Eigen::BDCSVD< _MatrixType >::MatrixVType |
Reimplemented from Eigen::SVDBase< BDCSVD< _MatrixType > >.
| typedef Matrix<RealScalar, Dynamic, Dynamic, ColMajor> Eigen::BDCSVD< _MatrixType >::MatrixXr |
| typedef NumTraits<typename MatrixType::Scalar>::Real Eigen::BDCSVD< _MatrixType >::RealScalar |
Reimplemented from Eigen::SVDBase< BDCSVD< _MatrixType > >.
| typedef MatrixType::Scalar Eigen::BDCSVD< _MatrixType >::Scalar |
Reimplemented from Eigen::SVDBase< BDCSVD< _MatrixType > >.
| typedef Base::SingularValuesType Eigen::BDCSVD< _MatrixType >::SingularValuesType |
Reimplemented from Eigen::SVDBase< BDCSVD< _MatrixType > >.
| typedef Matrix<RealScalar, Dynamic, 1> Eigen::BDCSVD< _MatrixType >::VectorType |
| anonymous enum |
| RowsAtCompileTime | |
| ColsAtCompileTime | |
| DiagSizeAtCompileTime | |
| MaxRowsAtCompileTime | |
| MaxColsAtCompileTime | |
| MaxDiagSizeAtCompileTime | |
| MatrixOptions |
Definition at line 67 of file BDCSVD.h.
{
RowsAtCompileTime = MatrixType::RowsAtCompileTime,
ColsAtCompileTime = MatrixType::ColsAtCompileTime,
DiagSizeAtCompileTime = EIGEN_SIZE_MIN_PREFER_DYNAMIC(RowsAtCompileTime, ColsAtCompileTime),
MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime,
MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime,
MaxDiagSizeAtCompileTime = EIGEN_SIZE_MIN_PREFER_FIXED(MaxRowsAtCompileTime, MaxColsAtCompileTime),
MatrixOptions = MatrixType::Options
};
| Eigen::BDCSVD< _MatrixType >::BDCSVD | ( | ) | [inline] |
Default Constructor.
The default constructor is useful in cases in which the user intends to perform decompositions via BDCSVD::compute(const MatrixType&).
Definition at line 94 of file BDCSVD.h.
: m_algoswap(16), m_numIters(0) {}
| Eigen::BDCSVD< _MatrixType >::BDCSVD | ( | Index | p_rows, |
| Index | p_cols, | ||
| unsigned int | computationOptions = 0 |
||
| ) | [inline] |
Default Constructor with memory preallocation.
Like the default constructor but with preallocation of the internal data according to the specified problem size.
Definition at line 104 of file BDCSVD.h.
: m_algoswap(16), m_numIters(0) { allocate(p_rows, p_cols, computationOptions); }
| Eigen::BDCSVD< _MatrixType >::BDCSVD | ( | const MatrixType & | matrix, |
| unsigned int | computationOptions = 0 |
||
| ) | [inline] |
Constructor performing the decomposition of given matrix.
| matrix | the matrix to decompose |
| computationOptions | optional parameter allowing to specify if you want full or thin U or V unitaries to be computed. By default, none is computed. This is a bit - field, the possible bits are ComputeFullU, ComputeThinU, ComputeFullV, ComputeThinV. |
Thin unitaries are only available if your matrix type has a Dynamic number of columns (for example MatrixXf). They also are not available with the (non - default) FullPivHouseholderQR preconditioner.
Definition at line 120 of file BDCSVD.h.
: m_algoswap(16), m_numIters(0) { compute(matrix, computationOptions); }
| Eigen::BDCSVD< _MatrixType >::~BDCSVD | ( | ) | [inline] |
| void Eigen::BDCSVD< MatrixType >::allocate | ( | Index | rows, |
| Index | cols, | ||
| unsigned int | computationOptions | ||
| ) | [private] |
Reimplemented from Eigen::SVDBase< BDCSVD< _MatrixType > >.
Definition at line 201 of file BDCSVD.h.
{
m_isTranspose = (p_cols > p_rows);
if (Base::allocate(p_rows, p_cols, computationOptions))
return;
m_computed = MatrixXr::Zero(m_diagSize + 1, m_diagSize );
m_compU = computeV();
m_compV = computeU();
if (m_isTranspose)
std::swap(m_compU, m_compV);
if (m_compU) m_naiveU = MatrixXr::Zero(m_diagSize + 1, m_diagSize + 1 );
else m_naiveU = MatrixXr::Zero(2, m_diagSize + 1 );
if (m_compV) m_naiveV = MatrixXr::Zero(m_diagSize, m_diagSize);
m_workspace.resize((m_diagSize+1)*(m_diagSize+1)*3);
m_workspaceI.resize(3*m_diagSize);
}// end allocate
| BDCSVD< MatrixType > & Eigen::BDCSVD< MatrixType >::compute | ( | const MatrixType & | matrix, |
| unsigned int | computationOptions | ||
| ) |
Method performing the decomposition of given matrix using custom options.
| matrix | the matrix to decompose |
| computationOptions | optional parameter allowing to specify if you want full or thin U or V unitaries to be computed. By default, none is computed. This is a bit - field, the possible bits are ComputeFullU, ComputeThinU, ComputeFullV, ComputeThinV. |
Thin unitaries are only available if your matrix type has a Dynamic number of columns (for example MatrixXf). They also are not available with the (non - default) FullPivHouseholderQR preconditioner.
Definition at line 224 of file BDCSVD.h.
{
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "\n\n\n======================================================================================================================\n\n\n";
#endif
allocate(matrix.rows(), matrix.cols(), computationOptions);
using std::abs;
//**** step -1 - If the problem is too small, directly falls back to JacobiSVD and return
if(matrix.cols() < m_algoswap)
{
// FIXME this line involves temporaries
JacobiSVD<MatrixType> jsvd(matrix,computationOptions);
if(computeU()) m_matrixU = jsvd.matrixU();
if(computeV()) m_matrixV = jsvd.matrixV();
m_singularValues = jsvd.singularValues();
m_nonzeroSingularValues = jsvd.nonzeroSingularValues();
m_isInitialized = true;
return *this;
}
//**** step 0 - Copy the input matrix and apply scaling to reduce over/under-flows
RealScalar scale = matrix.cwiseAbs().maxCoeff();
if(scale==RealScalar(0)) scale = RealScalar(1);
MatrixX copy;
if (m_isTranspose) copy = matrix.adjoint()/scale;
else copy = matrix/scale;
//**** step 1 - Bidiagonalization
// FIXME this line involves temporaries
internal::UpperBidiagonalization<MatrixX> bid(copy);
//**** step 2 - Divide & Conquer
m_naiveU.setZero();
m_naiveV.setZero();
// FIXME this line involves a temporary matrix
m_computed.topRows(m_diagSize) = bid.bidiagonal().toDenseMatrix().transpose();
m_computed.template bottomRows<1>().setZero();
divide(0, m_diagSize - 1, 0, 0, 0);
//**** step 3 - Copy singular values and vectors
for (int i=0; i<m_diagSize; i++)
{
RealScalar a = abs(m_computed.coeff(i, i));
m_singularValues.coeffRef(i) = a * scale;
if (a == 0)
{
m_nonzeroSingularValues = i;
m_singularValues.tail(m_diagSize - i - 1).setZero();
break;
}
else if (i == m_diagSize - 1)
{
m_nonzeroSingularValues = i + 1;
break;
}
}
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
// std::cout << "m_naiveU\n" << m_naiveU << "\n\n";
// std::cout << "m_naiveV\n" << m_naiveV << "\n\n";
#endif
if(m_isTranspose) copyUV(bid.householderV(), bid.householderU(), m_naiveV, m_naiveU);
else copyUV(bid.householderU(), bid.householderV(), m_naiveU, m_naiveV);
m_isInitialized = true;
return *this;
}// end compute
| BDCSVD& Eigen::BDCSVD< _MatrixType >::compute | ( | const MatrixType & | matrix | ) | [inline] |
Method performing the decomposition of given matrix using current options.
| matrix | the matrix to decompose |
This method uses the current computationOptions, as already passed to the constructor or to compute(const MatrixType&, unsigned int).
Definition at line 148 of file BDCSVD.h.
{
return compute(matrix, this->m_computationOptions);
}
| void Eigen::BDCSVD< MatrixType >::computeSingVals | ( | const ArrayRef & | col0, |
| const ArrayRef & | diag, | ||
| const IndicesRef & | perm, | ||
| VectorType & | singVals, | ||
| ArrayRef | shifts, | ||
| ArrayRef | mus | ||
| ) | [private] |
Definition at line 686 of file BDCSVD.h.
{
using std::abs;
using std::swap;
Index n = col0.size();
Index actual_n = n;
while(actual_n>1 && col0(actual_n-1)==0) --actual_n;
for (Index k = 0; k < n; ++k)
{
if (col0(k) == 0 || actual_n==1)
{
// if col0(k) == 0, then entry is deflated, so singular value is on diagonal
// if actual_n==1, then the deflated problem is already diagonalized
singVals(k) = k==0 ? col0(0) : diag(k);
mus(k) = 0;
shifts(k) = k==0 ? col0(0) : diag(k);
continue;
}
// otherwise, use secular equation to find singular value
RealScalar left = diag(k);
RealScalar right; // was: = (k != actual_n-1) ? diag(k+1) : (diag(actual_n-1) + col0.matrix().norm());
if(k==actual_n-1)
right = (diag(actual_n-1) + col0.matrix().norm());
else
{
// Skip deflated singular values
Index l = k+1;
while(col0(l)==0) { ++l; eigen_internal_assert(l<actual_n); }
right = diag(l);
}
// first decide whether it's closer to the left end or the right end
RealScalar mid = left + (right-left) / 2;
RealScalar fMid = secularEq(mid, col0, diag, perm, diag, 0);
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << right-left << "\n";
std::cout << "fMid = " << fMid << " " << secularEq(mid-left, col0, diag, perm, diag-left, left) << " " << secularEq(mid-right, col0, diag, perm, diag-right, right) << "\n";
std::cout << " = " << secularEq(0.1*(left+right), col0, diag, perm, diag, 0)
<< " " << secularEq(0.2*(left+right), col0, diag, perm, diag, 0)
<< " " << secularEq(0.3*(left+right), col0, diag, perm, diag, 0)
<< " " << secularEq(0.4*(left+right), col0, diag, perm, diag, 0)
<< " " << secularEq(0.49*(left+right), col0, diag, perm, diag, 0)
<< " " << secularEq(0.5*(left+right), col0, diag, perm, diag, 0)
<< " " << secularEq(0.51*(left+right), col0, diag, perm, diag, 0)
<< " " << secularEq(0.6*(left+right), col0, diag, perm, diag, 0)
<< " " << secularEq(0.7*(left+right), col0, diag, perm, diag, 0)
<< " " << secularEq(0.8*(left+right), col0, diag, perm, diag, 0)
<< " " << secularEq(0.9*(left+right), col0, diag, perm, diag, 0) << "\n";
#endif
RealScalar shift = (k == actual_n-1 || fMid > 0) ? left : right;
// measure everything relative to shift
Map<ArrayXr> diagShifted(m_workspace.data()+4*n, n);
diagShifted = diag - shift;
// initial guess
RealScalar muPrev, muCur;
if (shift == left)
{
muPrev = (right - left) * 0.1;
if (k == actual_n-1) muCur = right - left;
else muCur = (right - left) * 0.5;
}
else
{
muPrev = -(right - left) * 0.1;
muCur = -(right - left) * 0.5;
}
RealScalar fPrev = secularEq(muPrev, col0, diag, perm, diagShifted, shift);
RealScalar fCur = secularEq(muCur, col0, diag, perm, diagShifted, shift);
if (abs(fPrev) < abs(fCur))
{
swap(fPrev, fCur);
swap(muPrev, muCur);
}
// rational interpolation: fit a function of the form a / mu + b through the two previous
// iterates and use its zero to compute the next iterate
bool useBisection = fPrev*fCur>0;
while (fCur!=0 && abs(muCur - muPrev) > 8 * NumTraits<RealScalar>::epsilon() * numext::maxi<RealScalar>(abs(muCur), abs(muPrev)) && abs(fCur - fPrev)>NumTraits<RealScalar>::epsilon() && !useBisection)
{
++m_numIters;
// Find a and b such that the function f(mu) = a / mu + b matches the current and previous samples.
RealScalar a = (fCur - fPrev) / (1/muCur - 1/muPrev);
RealScalar b = fCur - a / muCur;
// And find mu such that f(mu)==0:
RealScalar muZero = -a/b;
RealScalar fZero = secularEq(muZero, col0, diag, perm, diagShifted, shift);
muPrev = muCur;
fPrev = fCur;
muCur = muZero;
fCur = fZero;
if (shift == left && (muCur < 0 || muCur > right - left)) useBisection = true;
if (shift == right && (muCur < -(right - left) || muCur > 0)) useBisection = true;
if (abs(fCur)>abs(fPrev)) useBisection = true;
}
// fall back on bisection method if rational interpolation did not work
if (useBisection)
{
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "useBisection for k = " << k << ", actual_n = " << actual_n << "\n";
#endif
RealScalar leftShifted, rightShifted;
if (shift == left)
{
leftShifted = RealScalar(1)/NumTraits<RealScalar>::highest();
// I don't understand why the case k==0 would be special there:
// if (k == 0) rightShifted = right - left; else
rightShifted = (k==actual_n-1) ? right : ((right - left) * 0.6); // theoretically we can take 0.5, but let's be safe
}
else
{
leftShifted = -(right - left) * 0.6;
rightShifted = -RealScalar(1)/NumTraits<RealScalar>::highest();
}
RealScalar fLeft = secularEq(leftShifted, col0, diag, perm, diagShifted, shift);
#if defined EIGEN_INTERNAL_DEBUGGING || defined EIGEN_BDCSVD_DEBUG_VERBOSE
RealScalar fRight = secularEq(rightShifted, col0, diag, perm, diagShifted, shift);
#endif
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
if(!(fLeft * fRight<0))
std::cout << k << " : " << fLeft << " * " << fRight << " == " << fLeft * fRight << " ; " << left << " - " << right << " -> " << leftShifted << " " << rightShifted << " shift=" << shift << "\n";
#endif
eigen_internal_assert(fLeft * fRight < 0);
while (rightShifted - leftShifted > 2 * NumTraits<RealScalar>::epsilon() * numext::maxi<RealScalar>(abs(leftShifted), abs(rightShifted)))
{
RealScalar midShifted = (leftShifted + rightShifted) / 2;
fMid = secularEq(midShifted, col0, diag, perm, diagShifted, shift);
if (fLeft * fMid < 0)
{
rightShifted = midShifted;
}
else
{
leftShifted = midShifted;
fLeft = fMid;
}
}
muCur = (leftShifted + rightShifted) / 2;
}
singVals[k] = shift + muCur;
shifts[k] = shift;
mus[k] = muCur;
// perturb singular value slightly if it equals diagonal entry to avoid division by zero later
// (deflation is supposed to avoid this from happening)
// - this does no seem to be necessary anymore -
// if (singVals[k] == left) singVals[k] *= 1 + NumTraits<RealScalar>::epsilon();
// if (singVals[k] == right) singVals[k] *= 1 - NumTraits<RealScalar>::epsilon();
}
}
| void Eigen::BDCSVD< MatrixType >::computeSingVecs | ( | const ArrayRef & | zhat, |
| const ArrayRef & | diag, | ||
| const IndicesRef & | perm, | ||
| const VectorType & | singVals, | ||
| const ArrayRef & | shifts, | ||
| const ArrayRef & | mus, | ||
| MatrixXr & | U, | ||
| MatrixXr & | V | ||
| ) | [private] |
Definition at line 907 of file BDCSVD.h.
{
Index n = zhat.size();
Index m = perm.size();
for (Index k = 0; k < n; ++k)
{
if (zhat(k) == 0)
{
U.col(k) = VectorType::Unit(n+1, k);
if (m_compV) V.col(k) = VectorType::Unit(n, k);
}
else
{
U.col(k).setZero();
for(Index l=0;l<m;++l)
{
Index i = perm(l);
U(i,k) = zhat(i)/(((diag(i) - shifts(k)) - mus(k)) )/( (diag(i) + singVals[k]));
}
U(n,k) = 0;
U.col(k).normalize();
if (m_compV)
{
V.col(k).setZero();
for(Index l=1;l<m;++l)
{
Index i = perm(l);
V(i,k) = diag(i) * zhat(i) / (((diag(i) - shifts(k)) - mus(k)) )/( (diag(i) + singVals[k]));
}
V(0,k) = -1;
V.col(k).normalize();
}
}
}
U.col(n) = VectorType::Unit(n+1, n);
}
| void Eigen::BDCSVD< MatrixType >::computeSVDofM | ( | Index | firstCol, |
| Index | n, | ||
| MatrixXr & | U, | ||
| VectorType & | singVals, | ||
| MatrixXr & | V | ||
| ) | [private] |
Definition at line 554 of file BDCSVD.h.
{
ArrayRef col0 = m_computed.col(firstCol).segment(firstCol, n);
m_workspace.head(n) = m_computed.block(firstCol, firstCol, n, n).diagonal();
ArrayRef diag = m_workspace.head(n);
diag(0) = 0;
// Allocate space for singular values and vectors
singVals.resize(n);
U.resize(n+1, n+1);
if (m_compV) V.resize(n, n);
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
if (col0.hasNaN() || diag.hasNaN())
std::cout << "\n\nHAS NAN\n\n";
#endif
// Many singular values might have been deflated, the zero ones have been moved to the end,
// but others are interleaved and we must ignore them at this stage.
// To this end, let's compute a permutation skipping them:
Index actual_n = n;
while(actual_n>1 && diag(actual_n-1)==0) --actual_n;
Index m = 0; // size of the deflated problem
for(Index k=0;k<actual_n;++k)
if(col0(k)!=0)
m_workspaceI(m++) = k;
Map<ArrayXi> perm(m_workspaceI.data(),m);
Map<ArrayXr> shifts(m_workspace.data()+1*n, n);
Map<ArrayXr> mus(m_workspace.data()+2*n, n);
Map<ArrayXr> zhat(m_workspace.data()+3*n, n);
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "computeSVDofM using:\n";
std::cout << " z: " << col0.transpose() << "\n";
std::cout << " d: " << diag.transpose() << "\n";
#endif
// Compute singVals, shifts, and mus
computeSingVals(col0, diag, perm, singVals, shifts, mus);
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << " j: " << (m_computed.block(firstCol, firstCol, n, n)).jacobiSvd().singularValues().transpose().reverse() << "\n\n";
std::cout << " sing-val: " << singVals.transpose() << "\n";
std::cout << " mu: " << mus.transpose() << "\n";
std::cout << " shift: " << shifts.transpose() << "\n";
{
Index actual_n = n;
while(actual_n>1 && col0(actual_n-1)==0) --actual_n;
std::cout << "\n\n mus: " << mus.head(actual_n).transpose() << "\n\n";
std::cout << " check1 (expect0) : " << ((singVals.array()-(shifts+mus)) / singVals.array()).head(actual_n).transpose() << "\n\n";
std::cout << " check2 (>0) : " << ((singVals.array()-diag) / singVals.array()).head(actual_n).transpose() << "\n\n";
std::cout << " check3 (>0) : " << ((diag.segment(1,actual_n-1)-singVals.head(actual_n-1).array()) / singVals.head(actual_n-1).array()).transpose() << "\n\n\n";
std::cout << " check4 (>0) : " << ((singVals.segment(1,actual_n-1)-singVals.head(actual_n-1))).transpose() << "\n\n\n";
}
#endif
#ifdef EIGEN_BDCSVD_SANITY_CHECKS
assert(singVals.allFinite());
assert(mus.allFinite());
assert(shifts.allFinite());
#endif
// Compute zhat
perturbCol0(col0, diag, perm, singVals, shifts, mus, zhat);
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << " zhat: " << zhat.transpose() << "\n";
#endif
#ifdef EIGEN_BDCSVD_SANITY_CHECKS
assert(zhat.allFinite());
#endif
computeSingVecs(zhat, diag, perm, singVals, shifts, mus, U, V);
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "U^T U: " << (U.transpose() * U - MatrixXr(MatrixXr::Identity(U.cols(),U.cols()))).norm() << "\n";
std::cout << "V^T V: " << (V.transpose() * V - MatrixXr(MatrixXr::Identity(V.cols(),V.cols()))).norm() << "\n";
#endif
#ifdef EIGEN_BDCSVD_SANITY_CHECKS
assert(U.allFinite());
assert(V.allFinite());
assert((U.transpose() * U - MatrixXr(MatrixXr::Identity(U.cols(),U.cols()))).norm() < 1e-14 * n);
assert((V.transpose() * V - MatrixXr(MatrixXr::Identity(V.cols(),V.cols()))).norm() < 1e-14 * n);
assert(m_naiveU.allFinite());
assert(m_naiveV.allFinite());
assert(m_computed.allFinite());
#endif
// Because of deflation, the singular values might not be completely sorted.
// Fortunately, reordering them is a O(n) problem
for(Index i=0; i<actual_n-1; ++i)
{
if(singVals(i)>singVals(i+1))
{
using std::swap;
swap(singVals(i),singVals(i+1));
U.col(i).swap(U.col(i+1));
if(m_compV) V.col(i).swap(V.col(i+1));
}
}
// Reverse order so that singular values in increased order
// Because of deflation, the zeros singular-values are already at the end
singVals.head(actual_n).reverseInPlace();
U.leftCols(actual_n).rowwise().reverseInPlace();
if (m_compV) V.leftCols(actual_n).rowwise().reverseInPlace();
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
JacobiSVD<MatrixXr> jsvd(m_computed.block(firstCol, firstCol, n, n) );
std::cout << " * j: " << jsvd.singularValues().transpose() << "\n\n";
std::cout << " * sing-val: " << singVals.transpose() << "\n";
// std::cout << " * err: " << ((jsvd.singularValues()-singVals)>1e-13*singVals.norm()).transpose() << "\n";
#endif
}
| void Eigen::BDCSVD< MatrixType >::copyUV | ( | const HouseholderU & | householderU, |
| const HouseholderV & | householderV, | ||
| const NaiveU & | naiveU, | ||
| const NaiveV & | naivev | ||
| ) | [private] |
Definition at line 296 of file BDCSVD.h.
{
// Note exchange of U and V: m_matrixU is set from m_naiveV and vice versa
if (computeU())
{
Index Ucols = m_computeThinU ? m_diagSize : householderU.cols();
m_matrixU = MatrixX::Identity(householderU.cols(), Ucols);
m_matrixU.topLeftCorner(m_diagSize, m_diagSize) = naiveV.template cast<Scalar>().topLeftCorner(m_diagSize, m_diagSize);
householderU.applyThisOnTheLeft(m_matrixU); // FIXME this line involves a temporary buffer
}
if (computeV())
{
Index Vcols = m_computeThinV ? m_diagSize : householderV.cols();
m_matrixV = MatrixX::Identity(householderV.cols(), Vcols);
m_matrixV.topLeftCorner(m_diagSize, m_diagSize) = naiveU.template cast<Scalar>().topLeftCorner(m_diagSize, m_diagSize);
householderV.applyThisOnTheLeft(m_matrixV); // FIXME this line involves a temporary buffer
}
}
| void Eigen::BDCSVD< MatrixType >::deflation | ( | Index | firstCol, |
| Index | lastCol, | ||
| Index | k, | ||
| Index | firstRowW, | ||
| Index | firstColW, | ||
| Index | shift | ||
| ) | [private] |
Definition at line 1021 of file BDCSVD.h.
{
using std::sqrt;
using std::abs;
const Index length = lastCol + 1 - firstCol;
Block<MatrixXr,Dynamic,1> col0(m_computed, firstCol+shift, firstCol+shift, length, 1);
Diagonal<MatrixXr> fulldiag(m_computed);
VectorBlock<Diagonal<MatrixXr>,Dynamic> diag(fulldiag, firstCol+shift, length);
RealScalar maxDiag = diag.tail((std::max)(Index(1),length-1)).cwiseAbs().maxCoeff();
RealScalar epsilon_strict = NumTraits<RealScalar>::epsilon() * maxDiag;
RealScalar epsilon_coarse = 8 * NumTraits<RealScalar>::epsilon() * numext::maxi<RealScalar>(col0.cwiseAbs().maxCoeff(), maxDiag);
#ifdef EIGEN_BDCSVD_SANITY_CHECKS
assert(m_naiveU.allFinite());
assert(m_naiveV.allFinite());
assert(m_computed.allFinite());
#endif
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "\ndeflate:" << diag.head(k+1).transpose() << " | " << diag.segment(k+1,length-k-1).transpose() << "\n";
#endif
//condition 4.1
if (diag(0) < epsilon_coarse)
{
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "deflation 4.1, because " << diag(0) << " < " << epsilon_coarse << "\n";
#endif
diag(0) = epsilon_coarse;
}
//condition 4.2
for (Index i=1;i<length;++i)
if (abs(col0(i)) < epsilon_strict)
{
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "deflation 4.2, set z(" << i << ") to zero because " << abs(col0(i)) << " < " << epsilon_strict << " (diag(" << i << ")=" << diag(i) << ")\n";
#endif
col0(i) = 0;
}
//condition 4.3
for (Index i=1;i<length; i++)
if (diag(i) < epsilon_coarse)
{
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "deflation 4.3, cancel z(" << i << ")=" << col0(i) << " because diag(" << i << ")=" << diag(i) << " < " << epsilon_coarse << "\n";
#endif
deflation43(firstCol, shift, i, length);
}
#ifdef EIGEN_BDCSVD_SANITY_CHECKS
assert(m_naiveU.allFinite());
assert(m_naiveV.allFinite());
assert(m_computed.allFinite());
#endif
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "to be sorted: " << diag.transpose() << "\n\n";
#endif
{
// Check for total deflation
// If we have a total deflation, then we have to consider col0(0)==diag(0) as a singular value during sorting
bool total_deflation = (col0.tail(length-1).array()==RealScalar(0)).all();
// Sort the diagonal entries, since diag(1:k-1) and diag(k:length) are already sorted, let's do a sorted merge.
// First, compute the respective permutation.
Index *permutation = m_workspaceI.data();
{
permutation[0] = 0;
Index p = 1;
// Move deflated diagonal entries at the end.
for(Index i=1; i<length; ++i)
if(diag(i)==0)
permutation[p++] = i;
Index i=1, j=k+1;
for( ; p < length; ++p)
{
if (i > k) permutation[p] = j++;
else if (j >= length) permutation[p] = i++;
else if (diag(i) < diag(j)) permutation[p] = j++;
else permutation[p] = i++;
}
}
// If we have a total deflation, then we have to insert diag(0) at the right place
if(total_deflation)
{
for(Index i=1; i<length; ++i)
{
Index pi = permutation[i];
if(diag(pi)==0 || diag(0)<diag(pi))
permutation[i-1] = permutation[i];
else
{
permutation[i-1] = 0;
break;
}
}
}
// Current index of each col, and current column of each index
Index *realInd = m_workspaceI.data()+length;
Index *realCol = m_workspaceI.data()+2*length;
for(int pos = 0; pos< length; pos++)
{
realCol[pos] = pos;
realInd[pos] = pos;
}
for(Index i = total_deflation?0:1; i < length; i++)
{
const Index pi = permutation[length - (total_deflation ? i+1 : i)];
const Index J = realCol[pi];
using std::swap;
// swap diagonal and first column entries:
swap(diag(i), diag(J));
if(i!=0 && J!=0) swap(col0(i), col0(J));
// change columns
if (m_compU) m_naiveU.col(firstCol+i).segment(firstCol, length + 1).swap(m_naiveU.col(firstCol+J).segment(firstCol, length + 1));
else m_naiveU.col(firstCol+i).segment(0, 2) .swap(m_naiveU.col(firstCol+J).segment(0, 2));
if (m_compV) m_naiveV.col(firstColW + i).segment(firstRowW, length).swap(m_naiveV.col(firstColW + J).segment(firstRowW, length));
//update real pos
const Index realI = realInd[i];
realCol[realI] = J;
realCol[pi] = i;
realInd[J] = realI;
realInd[i] = pi;
}
}
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "sorted: " << diag.transpose().format(bdcsvdfmt) << "\n";
std::cout << " : " << col0.transpose() << "\n\n";
#endif
//condition 4.4
{
Index i = length-1;
while(i>0 && (diag(i)==0 || col0(i)==0)) --i;
for(; i>1;--i)
if( (diag(i) - diag(i-1)) < NumTraits<RealScalar>::epsilon()*maxDiag )
{
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "deflation 4.4 with i = " << i << " because " << (diag(i) - diag(i-1)) << " < " << NumTraits<RealScalar>::epsilon()*diag(i) << "\n";
#endif
eigen_internal_assert(abs(diag(i) - diag(i-1))<epsilon_coarse && " diagonal entries are not properly sorted");
deflation44(firstCol, firstCol + shift, firstRowW, firstColW, i-1, i, length);
}
}
#ifdef EIGEN_BDCSVD_SANITY_CHECKS
for(Index j=2;j<length;++j)
assert(diag(j-1)<=diag(j) || diag(j)==0);
#endif
#ifdef EIGEN_BDCSVD_SANITY_CHECKS
assert(m_naiveU.allFinite());
assert(m_naiveV.allFinite());
assert(m_computed.allFinite());
#endif
}//end deflation
| void Eigen::BDCSVD< MatrixType >::deflation43 | ( | Index | firstCol, |
| Index | shift, | ||
| Index | i, | ||
| Index | size | ||
| ) | [private] |
Definition at line 952 of file BDCSVD.h.
{
using std::abs;
using std::sqrt;
using std::pow;
Index start = firstCol + shift;
RealScalar c = m_computed(start, start);
RealScalar s = m_computed(start+i, start);
RealScalar r = sqrt(numext::abs2(c) + numext::abs2(s));
if (r == 0)
{
m_computed(start+i, start+i) = 0;
return;
}
m_computed(start,start) = r;
m_computed(start+i, start) = 0;
m_computed(start+i, start+i) = 0;
JacobiRotation<RealScalar> J(c/r,-s/r);
if (m_compU) m_naiveU.middleRows(firstCol, size+1).applyOnTheRight(firstCol, firstCol+i, J);
else m_naiveU.applyOnTheRight(firstCol, firstCol+i, J);
}// end deflation 43
| void Eigen::BDCSVD< MatrixType >::deflation44 | ( | Index | firstColu, |
| Index | firstColm, | ||
| Index | firstRowW, | ||
| Index | firstColW, | ||
| Index | i, | ||
| Index | j, | ||
| Index | size | ||
| ) | [private] |
Definition at line 981 of file BDCSVD.h.
{
using std::abs;
using std::sqrt;
using std::conj;
using std::pow;
RealScalar c = m_computed(firstColm+i, firstColm);
RealScalar s = m_computed(firstColm+j, firstColm);
RealScalar r = sqrt(numext::abs2(c) + numext::abs2(s));
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "deflation 4.4: " << i << "," << j << " -> " << c << " " << s << " " << r << " ; "
<< m_computed(firstColm + i-1, firstColm) << " "
<< m_computed(firstColm + i, firstColm) << " "
<< m_computed(firstColm + i+1, firstColm) << " "
<< m_computed(firstColm + i+2, firstColm) << "\n";
std::cout << m_computed(firstColm + i-1, firstColm + i-1) << " "
<< m_computed(firstColm + i, firstColm+i) << " "
<< m_computed(firstColm + i+1, firstColm+i+1) << " "
<< m_computed(firstColm + i+2, firstColm+i+2) << "\n";
#endif
if (r==0)
{
m_computed(firstColm + i, firstColm + i) = m_computed(firstColm + j, firstColm + j);
return;
}
c/=r;
s/=r;
m_computed(firstColm + i, firstColm) = r;
m_computed(firstColm + j, firstColm + j) = m_computed(firstColm + i, firstColm + i);
m_computed(firstColm + j, firstColm) = 0;
JacobiRotation<RealScalar> J(c,-s);
if (m_compU) m_naiveU.middleRows(firstColu, size+1).applyOnTheRight(firstColu + i, firstColu + j, J);
else m_naiveU.applyOnTheRight(firstColu+i, firstColu+j, J);
if (m_compV) m_naiveV.middleRows(firstRowW, size).applyOnTheRight(firstColW + i, firstColW + j, J);
}// end deflation 44
| void Eigen::BDCSVD< MatrixType >::divide | ( | Index | firstCol, |
| Index | lastCol, | ||
| Index | firstRowW, | ||
| Index | firstColW, | ||
| Index | shift | ||
| ) | [private] |
Definition at line 375 of file BDCSVD.h.
{
// requires rows = cols + 1;
using std::pow;
using std::sqrt;
using std::abs;
const Index n = lastCol - firstCol + 1;
const Index k = n/2;
RealScalar alphaK;
RealScalar betaK;
RealScalar r0;
RealScalar lambda, phi, c0, s0;
VectorType l, f;
// We use the other algorithm which is more efficient for small
// matrices.
if (n < m_algoswap)
{
// FIXME this line involves temporaries
JacobiSVD<MatrixXr> b(m_computed.block(firstCol, firstCol, n + 1, n), ComputeFullU | (m_compV ? ComputeFullV : 0));
if (m_compU)
m_naiveU.block(firstCol, firstCol, n + 1, n + 1).real() = b.matrixU();
else
{
m_naiveU.row(0).segment(firstCol, n + 1).real() = b.matrixU().row(0);
m_naiveU.row(1).segment(firstCol, n + 1).real() = b.matrixU().row(n);
}
if (m_compV) m_naiveV.block(firstRowW, firstColW, n, n).real() = b.matrixV();
m_computed.block(firstCol + shift, firstCol + shift, n + 1, n).setZero();
m_computed.diagonal().segment(firstCol + shift, n) = b.singularValues().head(n);
return;
}
// We use the divide and conquer algorithm
alphaK = m_computed(firstCol + k, firstCol + k);
betaK = m_computed(firstCol + k + 1, firstCol + k);
// The divide must be done in that order in order to have good results. Divide change the data inside the submatrices
// and the divide of the right submatrice reads one column of the left submatrice. That's why we need to treat the
// right submatrix before the left one.
divide(k + 1 + firstCol, lastCol, k + 1 + firstRowW, k + 1 + firstColW, shift);
divide(firstCol, k - 1 + firstCol, firstRowW, firstColW + 1, shift + 1);
if (m_compU)
{
lambda = m_naiveU(firstCol + k, firstCol + k);
phi = m_naiveU(firstCol + k + 1, lastCol + 1);
}
else
{
lambda = m_naiveU(1, firstCol + k);
phi = m_naiveU(0, lastCol + 1);
}
r0 = sqrt((abs(alphaK * lambda) * abs(alphaK * lambda)) + abs(betaK * phi) * abs(betaK * phi));
if (m_compU)
{
l = m_naiveU.row(firstCol + k).segment(firstCol, k);
f = m_naiveU.row(firstCol + k + 1).segment(firstCol + k + 1, n - k - 1);
}
else
{
l = m_naiveU.row(1).segment(firstCol, k);
f = m_naiveU.row(0).segment(firstCol + k + 1, n - k - 1);
}
if (m_compV) m_naiveV(firstRowW+k, firstColW) = 1;
if (r0 == 0)
{
c0 = 1;
s0 = 0;
}
else
{
c0 = alphaK * lambda / r0;
s0 = betaK * phi / r0;
}
#ifdef EIGEN_BDCSVD_SANITY_CHECKS
assert(m_naiveU.allFinite());
assert(m_naiveV.allFinite());
assert(m_computed.allFinite());
#endif
if (m_compU)
{
MatrixXr q1 (m_naiveU.col(firstCol + k).segment(firstCol, k + 1));
// we shiftW Q1 to the right
for (Index i = firstCol + k - 1; i >= firstCol; i--)
m_naiveU.col(i + 1).segment(firstCol, k + 1) = m_naiveU.col(i).segment(firstCol, k + 1);
// we shift q1 at the left with a factor c0
m_naiveU.col(firstCol).segment( firstCol, k + 1) = (q1 * c0);
// last column = q1 * - s0
m_naiveU.col(lastCol + 1).segment(firstCol, k + 1) = (q1 * ( - s0));
// first column = q2 * s0
m_naiveU.col(firstCol).segment(firstCol + k + 1, n - k) = m_naiveU.col(lastCol + 1).segment(firstCol + k + 1, n - k) * s0;
// q2 *= c0
m_naiveU.col(lastCol + 1).segment(firstCol + k + 1, n - k) *= c0;
}
else
{
RealScalar q1 = m_naiveU(0, firstCol + k);
// we shift Q1 to the right
for (Index i = firstCol + k - 1; i >= firstCol; i--)
m_naiveU(0, i + 1) = m_naiveU(0, i);
// we shift q1 at the left with a factor c0
m_naiveU(0, firstCol) = (q1 * c0);
// last column = q1 * - s0
m_naiveU(0, lastCol + 1) = (q1 * ( - s0));
// first column = q2 * s0
m_naiveU(1, firstCol) = m_naiveU(1, lastCol + 1) *s0;
// q2 *= c0
m_naiveU(1, lastCol + 1) *= c0;
m_naiveU.row(1).segment(firstCol + 1, k).setZero();
m_naiveU.row(0).segment(firstCol + k + 1, n - k - 1).setZero();
}
#ifdef EIGEN_BDCSVD_SANITY_CHECKS
assert(m_naiveU.allFinite());
assert(m_naiveV.allFinite());
assert(m_computed.allFinite());
#endif
m_computed(firstCol + shift, firstCol + shift) = r0;
m_computed.col(firstCol + shift).segment(firstCol + shift + 1, k) = alphaK * l.transpose().real();
m_computed.col(firstCol + shift).segment(firstCol + shift + k + 1, n - k - 1) = betaK * f.transpose().real();
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
ArrayXr tmp1 = (m_computed.block(firstCol+shift, firstCol+shift, n, n)).jacobiSvd().singularValues();
#endif
// Second part: try to deflate singular values in combined matrix
deflation(firstCol, lastCol, k, firstRowW, firstColW, shift);
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
ArrayXr tmp2 = (m_computed.block(firstCol+shift, firstCol+shift, n, n)).jacobiSvd().singularValues();
std::cout << "\n\nj1 = " << tmp1.transpose().format(bdcsvdfmt) << "\n";
std::cout << "j2 = " << tmp2.transpose().format(bdcsvdfmt) << "\n\n";
std::cout << "err: " << ((tmp1-tmp2).abs()>1e-12*tmp2.abs()).transpose() << "\n";
static int count = 0;
std::cout << "# " << ++count << "\n\n";
assert((tmp1-tmp2).matrix().norm() < 1e-14*tmp2.matrix().norm());
// assert(count<681);
// assert(((tmp1-tmp2).abs()<1e-13*tmp2.abs()).all());
#endif
// Third part: compute SVD of combined matrix
MatrixXr UofSVD, VofSVD;
VectorType singVals;
computeSVDofM(firstCol + shift, n, UofSVD, singVals, VofSVD);
#ifdef EIGEN_BDCSVD_SANITY_CHECKS
assert(UofSVD.allFinite());
assert(VofSVD.allFinite());
#endif
if (m_compU)
structured_update(m_naiveU.block(firstCol, firstCol, n + 1, n + 1), UofSVD, (n+2)/2);
else
{
Map<Matrix<RealScalar,2,Dynamic>,Aligned> tmp(m_workspace.data(),2,n+1);
tmp.noalias() = m_naiveU.middleCols(firstCol, n+1) * UofSVD;
m_naiveU.middleCols(firstCol, n + 1) = tmp;
}
if (m_compV) structured_update(m_naiveV.block(firstRowW, firstColW, n, n), VofSVD, (n+1)/2);
#ifdef EIGEN_BDCSVD_SANITY_CHECKS
assert(m_naiveU.allFinite());
assert(m_naiveV.allFinite());
assert(m_computed.allFinite());
#endif
m_computed.block(firstCol + shift, firstCol + shift, n, n).setZero();
m_computed.block(firstCol + shift, firstCol + shift, n, n).diagonal() = singVals;
}// end divide
| void Eigen::BDCSVD< MatrixType >::perturbCol0 | ( | const ArrayRef & | col0, |
| const ArrayRef & | diag, | ||
| const IndicesRef & | perm, | ||
| const VectorType & | singVals, | ||
| const ArrayRef & | shifts, | ||
| const ArrayRef & | mus, | ||
| ArrayRef | zhat | ||
| ) | [private] |
Definition at line 858 of file BDCSVD.h.
{
using std::sqrt;
Index n = col0.size();
Index m = perm.size();
if(m==0)
{
zhat.setZero();
return;
}
Index last = perm(m-1);
// The offset permits to skip deflated entries while computing zhat
for (Index k = 0; k < n; ++k)
{
if (col0(k) == 0) // deflated
zhat(k) = 0;
else
{
// see equation (3.6)
RealScalar dk = diag(k);
RealScalar prod = (singVals(last) + dk) * (mus(last) + (shifts(last) - dk));
for(Index l = 0; l<m; ++l)
{
Index i = perm(l);
if(i!=k)
{
Index j = i<k ? i : perm(l-1);
prod *= ((singVals(j)+dk) / ((diag(i)+dk))) * ((mus(j)+(shifts(j)-dk)) / ((diag(i)-dk)));
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
if(i!=k && std::abs(((singVals(j)+dk)*(mus(j)+(shifts(j)-dk)))/((diag(i)+dk)*(diag(i)-dk)) - 1) > 0.9 )
std::cout << " " << ((singVals(j)+dk)*(mus(j)+(shifts(j)-dk)))/((diag(i)+dk)*(diag(i)-dk)) << " == (" << (singVals(j)+dk) << " * " << (mus(j)+(shifts(j)-dk))
<< ") / (" << (diag(i)+dk) << " * " << (diag(i)-dk) << ")\n";
#endif
}
}
#ifdef EIGEN_BDCSVD_DEBUG_VERBOSE
std::cout << "zhat(" << k << ") = sqrt( " << prod << ") ; " << (singVals(last) + dk) << " * " << mus(last) + shifts(last) << " - " << dk << "\n";
#endif
RealScalar tmp = sqrt(prod);
zhat(k) = col0(k) > 0 ? tmp : -tmp;
}
}
}
| BDCSVD< MatrixType >::RealScalar Eigen::BDCSVD< MatrixType >::secularEq | ( | RealScalar | x, |
| const ArrayRef & | col0, | ||
| const ArrayRef & | diag, | ||
| const IndicesRef & | perm, | ||
| const ArrayRef & | diagShifted, | ||
| RealScalar | shift | ||
| ) | [static, private] |
Definition at line 673 of file BDCSVD.h.
{
Index m = perm.size();
RealScalar res = 1;
for(Index i=0; i<m; ++i)
{
Index j = perm(i);
res += numext::abs2(col0(j)) / ((diagShifted(j) - mu) * (diag(j) + shift + mu));
}
return res;
}
| void Eigen::BDCSVD< _MatrixType >::setSwitchSize | ( | int | s | ) | [inline] |
Definition at line 153 of file BDCSVD.h.
{
eigen_assert(s>3 && "BDCSVD the size of the algo switch has to be greater than 3");
m_algoswap = s;
}
| void Eigen::BDCSVD< MatrixType >::structured_update | ( | Block< MatrixXr, Dynamic, Dynamic > | A, |
| const MatrixXr & | B, | ||
| Index | n1 | ||
| ) | [private] |
Performs A = A * B exploiting the special structure of the matrix A. Splitting A as: A = [A1] [A2] such that A1.rows()==n1, then we assume that at least half of the columns of A1 and A2 are zeros. We can thus pack them prior to the the matrix product. However, this is only worth the effort if the matrix is large enough.
Definition at line 324 of file BDCSVD.h.
{
Index n = A.rows();
if(n>100)
{
// If the matrices are large enough, let's exploit the sparse structure of A by
// splitting it in half (wrt n1), and packing the non-zero columns.
Index n2 = n - n1;
Map<MatrixXr> A1(m_workspace.data() , n1, n);
Map<MatrixXr> A2(m_workspace.data()+ n1*n, n2, n);
Map<MatrixXr> B1(m_workspace.data()+ n*n, n, n);
Map<MatrixXr> B2(m_workspace.data()+2*n*n, n, n);
Index k1=0, k2=0;
for(Index j=0; j<n; ++j)
{
if( (A.col(j).head(n1).array()!=0).any() )
{
A1.col(k1) = A.col(j).head(n1);
B1.row(k1) = B.row(j);
++k1;
}
if( (A.col(j).tail(n2).array()!=0).any() )
{
A2.col(k2) = A.col(j).tail(n2);
B2.row(k2) = B.row(j);
++k2;
}
}
A.topRows(n1).noalias() = A1.leftCols(k1) * B1.topRows(k1);
A.bottomRows(n2).noalias() = A2.leftCols(k2) * B2.topRows(k2);
}
else
{
Map<MatrixXr,Aligned> tmp(m_workspace.data(),n,n);
tmp.noalias() = A*B;
A = tmp;
}
}
int Eigen::BDCSVD< _MatrixType >::m_algoswap [protected] |
bool Eigen::BDCSVD< _MatrixType >::m_compU [protected] |
MatrixXr Eigen::BDCSVD< _MatrixType >::m_computed [protected] |
bool Eigen::BDCSVD< _MatrixType >::m_compV [protected] |
bool Eigen::BDCSVD< _MatrixType >::m_isTranspose [protected] |
MatrixXr Eigen::BDCSVD< _MatrixType >::m_naiveU [protected] |
MatrixXr Eigen::BDCSVD< _MatrixType >::m_naiveV [protected] |
Index Eigen::BDCSVD< _MatrixType >::m_nRec [protected] |
| int Eigen::BDCSVD< _MatrixType >::m_numIters |
ArrayXr Eigen::BDCSVD< _MatrixType >::m_workspace [protected] |
ArrayXi Eigen::BDCSVD< _MatrixType >::m_workspaceI [protected] |