Householder rank-revealing QR decomposition of a matrix with full pivoting. More...

#include <FullPivHouseholderQR.h>

Inheritance diagram for Eigen::FullPivHouseholderQR< _MatrixType >:

Collaboration diagram for Eigen::FullPivHouseholderQR< _MatrixType >:

Public Types
enum	{ RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, Options = MatrixType::Options, MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }
typedef _MatrixType	MatrixType
typedef MatrixType::Scalar	Scalar
typedef MatrixType::RealScalar	RealScalar
typedef MatrixType::StorageIndex	StorageIndex
typedef internal::FullPivHouseholderQRMatrixQReturnType < MatrixType >	MatrixQReturnType
typedef internal::plain_diag_type < MatrixType >::type	HCoeffsType
typedef Matrix< StorageIndex, 1, EIGEN_SIZE_MIN_PREFER_DYNAMIC(ColsAtCompileTime, RowsAtCompileTime), RowMajor, 1, EIGEN_SIZE_MIN_PREFER_FIXED(MaxColsAtCompileTime, MaxRowsAtCompileTime)>	IntDiagSizeVectorType
typedef PermutationMatrix < ColsAtCompileTime, MaxColsAtCompileTime >	PermutationType
typedef internal::plain_row_type < MatrixType >::type	RowVectorType
typedef internal::plain_col_type < MatrixType >::type	ColVectorType
typedef MatrixType::PlainObject	PlainObject
Public Member Functions
	FullPivHouseholderQR ()
	Default Constructor.
	FullPivHouseholderQR (Index rows, Index cols)
	Default Constructor with memory preallocation.
template<typename InputType >
	FullPivHouseholderQR (const EigenBase< InputType > &matrix)
	Constructs a QR factorization from a given matrix.
template<typename Rhs >
const Solve < FullPivHouseholderQR, Rhs >	solve (const MatrixBase< Rhs > &b) const
MatrixQReturnType	matrixQ (void) const
const MatrixType &	matrixQR () const
template<typename InputType >
FullPivHouseholderQR &	compute (const EigenBase< InputType > &matrix)
const PermutationType &	colsPermutation () const
const IntDiagSizeVectorType &	rowsTranspositions () const
MatrixType::RealScalar	absDeterminant () const
MatrixType::RealScalar	logAbsDeterminant () const
Index	rank () const
Index	dimensionOfKernel () const
bool	isInjective () const
bool	isSurjective () const
bool	isInvertible () const
const Inverse < FullPivHouseholderQR >	inverse () const
Index	rows () const
Index	cols () const
const HCoeffsType &	hCoeffs () const
FullPivHouseholderQR &	setThreshold (const RealScalar &threshold)
FullPivHouseholderQR &	setThreshold (Default_t)
RealScalar	threshold () const
Index	nonzeroPivots () const
RealScalar	maxPivot () const
template<typename RhsType , typename DstType >
EIGEN_DEVICE_FUNC void	_solve_impl (const RhsType &rhs, DstType &dst) const
Protected Member Functions
void	computeInPlace ()
Static Protected Member Functions
static void	check_template_parameters ()
Protected Attributes
MatrixType	m_qr
HCoeffsType	m_hCoeffs
IntDiagSizeVectorType	m_rows_transpositions
IntDiagSizeVectorType	m_cols_transpositions
PermutationType	m_cols_permutation
RowVectorType	m_temp
bool	m_isInitialized
bool	m_usePrescribedThreshold
RealScalar	m_prescribedThreshold
RealScalar	m_maxpivot
Index	m_nonzero_pivots
RealScalar	m_precision
Index	m_det_pq

Detailed Description

template<typename _MatrixType>
class Eigen::FullPivHouseholderQR< _MatrixType >

Householder rank-revealing QR decomposition of a matrix with full pivoting.

Template Parameters:

_MatrixType the type of the matrix of which we are computing the QR decomposition

This class performs a rank-revealing QR decomposition of a matrix A into matrices P, P', Q and R such that

$\mathbf{P} \, \mathbf{A} \, \mathbf{P}' = \mathbf{Q} \, \mathbf{R}$

by using Householder transformations. Here, P and P' are permutation matrices, Q a unitary matrix and R an upper triangular matrix.

This decomposition performs a very prudent full pivoting in order to be rank-revealing and achieve optimal numerical stability. The trade-off is that it is slower than HouseholderQR and ColPivHouseholderQR.

See also:: MatrixBase::fullPivHouseholderQr()

Definition at line 55 of file FullPivHouseholderQR.h.

Member Typedef Documentation

template<typename _MatrixType>

typedef internal::plain_col_type<MatrixType>::type Eigen::FullPivHouseholderQR< _MatrixType >::ColVectorType

Definition at line 78 of file FullPivHouseholderQR.h.

template<typename _MatrixType>

typedef internal::plain_diag_type<MatrixType>::type Eigen::FullPivHouseholderQR< _MatrixType >::HCoeffsType

Definition at line 72 of file FullPivHouseholderQR.h.

template<typename _MatrixType>

typedef Matrix<StorageIndex, 1, EIGEN_SIZE_MIN_PREFER_DYNAMIC(ColsAtCompileTime,RowsAtCompileTime), RowMajor, 1, EIGEN_SIZE_MIN_PREFER_FIXED(MaxColsAtCompileTime,MaxRowsAtCompileTime)> Eigen::FullPivHouseholderQR< _MatrixType >::IntDiagSizeVectorType

Definition at line 75 of file FullPivHouseholderQR.h.

template<typename _MatrixType>

typedef internal::FullPivHouseholderQRMatrixQReturnType<MatrixType> Eigen::FullPivHouseholderQR< _MatrixType >::MatrixQReturnType

Definition at line 71 of file FullPivHouseholderQR.h.

template<typename _MatrixType>

typedef _MatrixType Eigen::FullPivHouseholderQR< _MatrixType >::MatrixType

Definition at line 59 of file FullPivHouseholderQR.h.

template<typename _MatrixType>

typedef PermutationMatrix<ColsAtCompileTime, MaxColsAtCompileTime> Eigen::FullPivHouseholderQR< _MatrixType >::PermutationType

Definition at line 76 of file FullPivHouseholderQR.h.

template<typename _MatrixType>

typedef MatrixType::PlainObject Eigen::FullPivHouseholderQR< _MatrixType >::PlainObject

Definition at line 79 of file FullPivHouseholderQR.h.

template<typename _MatrixType>

typedef MatrixType::RealScalar Eigen::FullPivHouseholderQR< _MatrixType >::RealScalar

Definition at line 68 of file FullPivHouseholderQR.h.

template<typename _MatrixType>

typedef internal::plain_row_type<MatrixType>::type Eigen::FullPivHouseholderQR< _MatrixType >::RowVectorType

Definition at line 77 of file FullPivHouseholderQR.h.

template<typename _MatrixType>

typedef MatrixType::Scalar Eigen::FullPivHouseholderQR< _MatrixType >::Scalar

Definition at line 67 of file FullPivHouseholderQR.h.

template<typename _MatrixType>

typedef MatrixType::StorageIndex Eigen::FullPivHouseholderQR< _MatrixType >::StorageIndex

Definition at line 70 of file FullPivHouseholderQR.h.

Member Enumeration Documentation

template<typename _MatrixType>

anonymous enum

Enumerator:

RowsAtCompileTime
ColsAtCompileTime
Options
MaxRowsAtCompileTime
MaxColsAtCompileTime

Definition at line 60 of file FullPivHouseholderQR.h.

         {
      RowsAtCompileTime = MatrixType::RowsAtCompileTime,
      ColsAtCompileTime = MatrixType::ColsAtCompileTime,
      Options = MatrixType::Options,
      MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime,
      MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime
    };

Constructor & Destructor Documentation

template<typename _MatrixType>

Eigen::FullPivHouseholderQR< _MatrixType >::FullPivHouseholderQR ( ) [inline]

Default Constructor.

The default constructor is useful in cases in which the user intends to perform decompositions via FullPivHouseholderQR::compute(const MatrixType&).

Definition at line 86 of file FullPivHouseholderQR.h.

      : m_qr(),
        m_hCoeffs(),
        m_rows_transpositions(),
        m_cols_transpositions(),
        m_cols_permutation(),
        m_temp(),
        m_isInitialized(false),
        m_usePrescribedThreshold(false) {}

template<typename _MatrixType>

Eigen::FullPivHouseholderQR< _MatrixType >::FullPivHouseholderQR	(	Index	rows,
		Index	cols
	)		`[inline]`

Default Constructor with memory preallocation.

Like the default constructor but with preallocation of the internal data according to the specified problem size.

See also:: FullPivHouseholderQR()

Definition at line 102 of file FullPivHouseholderQR.h.

      : m_qr(rows, cols),
        m_hCoeffs((std::min)(rows,cols)),
        m_rows_transpositions((std::min)(rows,cols)),
        m_cols_transpositions((std::min)(rows,cols)),
        m_cols_permutation(cols),
        m_temp(cols),
        m_isInitialized(false),
        m_usePrescribedThreshold(false) {}

template<typename _MatrixType>

template<typename InputType >

Eigen::FullPivHouseholderQR< _MatrixType >::FullPivHouseholderQR ( const EigenBase< InputType > & matrix ) [inline, explicit]

Constructs a QR factorization from a given matrix.

This constructor computes the QR factorization of the matrix matrix by calling the method compute(). It is a short cut for:

 FullPivHouseholderQR<MatrixType> qr(matrix.rows(), matrix.cols());
 qr.compute(matrix);

See also:: compute()

Definition at line 125 of file FullPivHouseholderQR.h.

      : m_qr(matrix.rows(), matrix.cols()),
        m_hCoeffs((std::min)(matrix.rows(), matrix.cols())),
        m_rows_transpositions((std::min)(matrix.rows(), matrix.cols())),
        m_cols_transpositions((std::min)(matrix.rows(), matrix.cols())),
        m_cols_permutation(matrix.cols()),
        m_temp(matrix.cols()),
        m_isInitialized(false),
        m_usePrescribedThreshold(false)
    {
      compute(matrix.derived());
    }

Member Function Documentation

template<typename _MatrixType >

template<typename RhsType , typename DstType >

void Eigen::FullPivHouseholderQR< _MatrixType >::_solve_impl	(	const RhsType &	rhs,
		DstType &	dst
	)		const

Definition at line 526 of file FullPivHouseholderQR.h.

{
  eigen_assert(rhs.rows() == rows());
  const Index l_rank = rank();

  // FIXME introduce nonzeroPivots() and use it here. and more generally,
  // make the same improvements in this dec as in FullPivLU.
  if(l_rank==0)
  {
    dst.setZero();
    return;
  }

  typename RhsType::PlainObject c(rhs);

  Matrix<Scalar,1,RhsType::ColsAtCompileTime> temp(rhs.cols());
  for (Index k = 0; k < l_rank; ++k)
  {
    Index remainingSize = rows()-k;
    c.row(k).swap(c.row(m_rows_transpositions.coeff(k)));
    c.bottomRightCorner(remainingSize, rhs.cols())
      .applyHouseholderOnTheLeft(m_qr.col(k).tail(remainingSize-1),
                               m_hCoeffs.coeff(k), &temp.coeffRef(0));
  }

  m_qr.topLeftCorner(l_rank, l_rank)
      .template triangularView<Upper>()
      .solveInPlace(c.topRows(l_rank));

  for(Index i = 0; i < l_rank; ++i) dst.row(m_cols_permutation.indices().coeff(i)) = c.row(i);
  for(Index i = l_rank; i < cols(); ++i) dst.row(m_cols_permutation.indices().coeff(i)).setZero();
}

template<typename MatrixType >

MatrixType::RealScalar Eigen::FullPivHouseholderQR< MatrixType >::absDeterminant ( ) const

Returns:: the absolute value of the determinant of the matrix of which *this is the QR decomposition. It has only linear complexity (that is, O(n) where n is the dimension of the square matrix) as the QR decomposition has already been computed.

Note:: This is only for square matrices.

Warning:: a determinant can be very big or small, so for matrices of large enough dimension, there is a risk of overflow/underflow. One way to work around that is to use logAbsDeterminant() instead.

See also:: logAbsDeterminant(), MatrixBase::determinant()

Definition at line 407 of file FullPivHouseholderQR.h.

{
  using std::abs;
  eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
  eigen_assert(m_qr.rows() == m_qr.cols() && "You can't take the determinant of a non-square matrix!");
  return abs(m_qr.diagonal().prod());
}

template<typename _MatrixType>

static void Eigen::FullPivHouseholderQR< _MatrixType >::check_template_parameters ( ) [inline, static, protected]

Definition at line 386 of file FullPivHouseholderQR.h.

    {
      EIGEN_STATIC_ASSERT_NON_INTEGER(Scalar);
    }

template<typename _MatrixType>

Index Eigen::FullPivHouseholderQR< _MatrixType >::cols ( void ) const [inline]

Definition at line 301 of file FullPivHouseholderQR.h.

{ return m_qr.cols(); }

template<typename _MatrixType>

const PermutationType& Eigen::FullPivHouseholderQR< _MatrixType >::colsPermutation ( ) const [inline]

Returns:: a const reference to the column permutation matrix

Definition at line 180 of file FullPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
      return m_cols_permutation;
    }

template<typename MatrixType >

template<typename InputType >

FullPivHouseholderQR< MatrixType > & Eigen::FullPivHouseholderQR< MatrixType >::compute ( const EigenBase< InputType > & matrix )

Performs the QR factorization of the given matrix matrix. The result of the factorization is stored into *this, and a reference to *this is returned.

See also:: class FullPivHouseholderQR, FullPivHouseholderQR(const MatrixType&)

Definition at line 431 of file FullPivHouseholderQR.h.

{
  check_template_parameters();
  
  m_qr = matrix.derived();
  
  computeInPlace();
  
  return *this;
}

template<typename MatrixType >

void Eigen::FullPivHouseholderQR< MatrixType >::computeInPlace ( ) [protected]

Definition at line 443 of file FullPivHouseholderQR.h.

{
  using std::abs;
  Index rows = m_qr.rows();
  Index cols = m_qr.cols();
  Index size = (std::min)(rows,cols);

  
  m_hCoeffs.resize(size);

  m_temp.resize(cols);

  m_precision = NumTraits<Scalar>::epsilon() * RealScalar(size);

  m_rows_transpositions.resize(size);
  m_cols_transpositions.resize(size);
  Index number_of_transpositions = 0;

  RealScalar biggest(0);

  m_nonzero_pivots = size; // the generic case is that in which all pivots are nonzero (invertible case)
  m_maxpivot = RealScalar(0);

  for (Index k = 0; k < size; ++k)
  {
    Index row_of_biggest_in_corner, col_of_biggest_in_corner;
    typedef internal::scalar_score_coeff_op<Scalar> Scoring;
    typedef typename Scoring::result_type Score;

    Score score = m_qr.bottomRightCorner(rows-k, cols-k)
                      .unaryExpr(Scoring())
                      .maxCoeff(&row_of_biggest_in_corner, &col_of_biggest_in_corner);
    row_of_biggest_in_corner += k;
    col_of_biggest_in_corner += k;
    RealScalar biggest_in_corner = internal::abs_knowing_score<Scalar>()(m_qr(row_of_biggest_in_corner, col_of_biggest_in_corner), score);
    if(k==0) biggest = biggest_in_corner;

    // if the corner is negligible, then we have less than full rank, and we can finish early
    if(internal::isMuchSmallerThan(biggest_in_corner, biggest, m_precision))
    {
      m_nonzero_pivots = k;
      for(Index i = k; i < size; i++)
      {
        m_rows_transpositions.coeffRef(i) = i;
        m_cols_transpositions.coeffRef(i) = i;
        m_hCoeffs.coeffRef(i) = Scalar(0);
      }
      break;
    }

    m_rows_transpositions.coeffRef(k) = row_of_biggest_in_corner;
    m_cols_transpositions.coeffRef(k) = col_of_biggest_in_corner;
    if(k != row_of_biggest_in_corner) {
      m_qr.row(k).tail(cols-k).swap(m_qr.row(row_of_biggest_in_corner).tail(cols-k));
      ++number_of_transpositions;
    }
    if(k != col_of_biggest_in_corner) {
      m_qr.col(k).swap(m_qr.col(col_of_biggest_in_corner));
      ++number_of_transpositions;
    }

    RealScalar beta;
    m_qr.col(k).tail(rows-k).makeHouseholderInPlace(m_hCoeffs.coeffRef(k), beta);
    m_qr.coeffRef(k,k) = beta;

    // remember the maximum absolute value of diagonal coefficients
    if(abs(beta) > m_maxpivot) m_maxpivot = abs(beta);

    m_qr.bottomRightCorner(rows-k, cols-k-1)
        .applyHouseholderOnTheLeft(m_qr.col(k).tail(rows-k-1), m_hCoeffs.coeffRef(k), &m_temp.coeffRef(k+1));
  }

  m_cols_permutation.setIdentity(cols);
  for(Index k = 0; k < size; ++k)
    m_cols_permutation.applyTranspositionOnTheRight(k, m_cols_transpositions.coeff(k));

  m_det_pq = (number_of_transpositions%2) ? -1 : 1;
  m_isInitialized = true;
}

template<typename _MatrixType>

Index Eigen::FullPivHouseholderQR< _MatrixType >::dimensionOfKernel ( ) const [inline]

Returns:: the dimension of the kernel of the matrix of which *this is the QR decomposition.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 245 of file FullPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
      return cols() - rank();
    }

template<typename _MatrixType>

const HCoeffsType& Eigen::FullPivHouseholderQR< _MatrixType >::hCoeffs ( ) const [inline]

Returns:: a const reference to the vector of Householder coefficients used to represent the factor Q.

For advanced uses only.

Definition at line 307 of file FullPivHouseholderQR.h.

{ return m_hCoeffs; }

template<typename _MatrixType>

const Inverse<FullPivHouseholderQR> Eigen::FullPivHouseholderQR< _MatrixType >::inverse ( ) const [inline]

Returns:: the inverse of the matrix of which *this is the QR decomposition.

Note:: If this matrix is not invertible, the returned matrix has undefined coefficients. Use isInvertible() to first determine whether this matrix is invertible.

Definition at line 294 of file FullPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
      return Inverse<FullPivHouseholderQR>(*this);
    }

template<typename _MatrixType>

bool Eigen::FullPivHouseholderQR< _MatrixType >::isInjective ( ) const [inline]

Returns:: true if the matrix of which *this is the QR decomposition represents an injective linear map, i.e. has trivial kernel; false otherwise.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 258 of file FullPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
      return rank() == cols();
    }

template<typename _MatrixType>

bool Eigen::FullPivHouseholderQR< _MatrixType >::isInvertible ( ) const [inline]

Returns:: true if the matrix of which *this is the QR decomposition is invertible.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 283 of file FullPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
      return isInjective() && isSurjective();
    }

template<typename _MatrixType>

bool Eigen::FullPivHouseholderQR< _MatrixType >::isSurjective ( ) const [inline]

Returns:: true if the matrix of which *this is the QR decomposition represents a surjective linear map; false otherwise.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 271 of file FullPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
      return rank() == rows();
    }

template<typename MatrixType >

MatrixType::RealScalar Eigen::FullPivHouseholderQR< MatrixType >::logAbsDeterminant ( ) const

Returns:: the natural log of the absolute value of the determinant of the matrix of which *this is the QR decomposition. It has only linear complexity (that is, O(n) where n is the dimension of the square matrix) as the QR decomposition has already been computed.

Note:: This is only for square matrices.; This method is useful to work around the risk of overflow/underflow that's inherent to determinant computation.

See also:: absDeterminant(), MatrixBase::determinant()

Definition at line 416 of file FullPivHouseholderQR.h.

{
  eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
  eigen_assert(m_qr.rows() == m_qr.cols() && "You can't take the determinant of a non-square matrix!");
  return m_qr.diagonal().cwiseAbs().array().log().sum();
}

template<typename MatrixType >

FullPivHouseholderQR< MatrixType >::MatrixQReturnType Eigen::FullPivHouseholderQR< MatrixType >::matrixQ ( void ) const [inline]

Returns:: Expression object representing the matrix Q

Definition at line 641 of file FullPivHouseholderQR.h.

{
  eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
  return MatrixQReturnType(m_qr, m_hCoeffs, m_rows_transpositions);
}

template<typename _MatrixType>

const MatrixType& Eigen::FullPivHouseholderQR< _MatrixType >::matrixQR ( ) const [inline]

Returns:: a reference to the matrix where the Householder QR decomposition is stored

Definition at line 170 of file FullPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
      return m_qr;
    }

template<typename _MatrixType>

RealScalar Eigen::FullPivHouseholderQR< _MatrixType >::maxPivot ( ) const [inline]

Returns:: the absolute value of the biggest pivot, i.e. the biggest diagonal coefficient of U.

Definition at line 376 of file FullPivHouseholderQR.h.

{ return m_maxpivot; }

template<typename _MatrixType>

Index Eigen::FullPivHouseholderQR< _MatrixType >::nonzeroPivots ( ) const [inline]

Returns:: the number of nonzero pivots in the QR decomposition. Here nonzero is meant in the exact sense, not in a fuzzy sense. So that notion isn't really intrinsically interesting, but it is still useful when implementing algorithms.

See also:: rank()

Definition at line 367 of file FullPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "LU is not initialized.");
      return m_nonzero_pivots;
    }

template<typename _MatrixType>

Index Eigen::FullPivHouseholderQR< _MatrixType >::rank ( ) const [inline]

Returns:: the rank of the matrix of which *this is the QR decomposition.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 228 of file FullPivHouseholderQR.h.

    {
      using std::abs;
      eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
      RealScalar premultiplied_threshold = abs(m_maxpivot) * threshold();
      Index result = 0;
      for(Index i = 0; i < m_nonzero_pivots; ++i)
        result += (abs(m_qr.coeff(i,i)) > premultiplied_threshold);
      return result;
    }

template<typename _MatrixType>

Index Eigen::FullPivHouseholderQR< _MatrixType >::rows ( void ) const [inline]

Definition at line 300 of file FullPivHouseholderQR.h.

{ return m_qr.rows(); }

template<typename _MatrixType>

const IntDiagSizeVectorType& Eigen::FullPivHouseholderQR< _MatrixType >::rowsTranspositions ( ) const [inline]

Returns:: a const reference to the vector of indices representing the rows transpositions

Definition at line 187 of file FullPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
      return m_rows_transpositions;
    }

template<typename _MatrixType>

FullPivHouseholderQR& Eigen::FullPivHouseholderQR< _MatrixType >::setThreshold ( const RealScalar & threshold ) [inline]

Allows to prescribe a threshold to be used by certain methods, such as rank(), who need to determine when pivots are to be considered nonzero. This is not used for the QR decomposition itself.

When it needs to get the threshold value, Eigen calls threshold(). By default, this uses a formula to automatically determine a reasonable threshold. Once you have called the present method setThreshold(const RealScalar&), your value is used instead.

Parameters:

threshold The new value to use as the threshold.

A pivot will be considered nonzero if its absolute value is strictly greater than 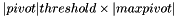$\vert pivot \vert \leqslant threshold \times \vert maxpivot \vert$ where maxpivot is the biggest pivot.

If you want to come back to the default behavior, call setThreshold(Default_t)

Definition at line 326 of file FullPivHouseholderQR.h.

    {
      m_usePrescribedThreshold = true;
      m_prescribedThreshold = threshold;
      return *this;
    }

template<typename _MatrixType>

FullPivHouseholderQR& Eigen::FullPivHouseholderQR< _MatrixType >::setThreshold ( Default_t ) [inline]

Allows to come back to the default behavior, letting Eigen use its default formula for determining the threshold.

You should pass the special object Eigen::Default as parameter here.

 qr.setThreshold(Eigen::Default);

See the documentation of setThreshold(const RealScalar&).

Definition at line 341 of file FullPivHouseholderQR.h.

    {
      m_usePrescribedThreshold = false;
      return *this;
    }

template<typename _MatrixType>

template<typename Rhs >

const Solve<FullPivHouseholderQR, Rhs> Eigen::FullPivHouseholderQR< _MatrixType >::solve ( const MatrixBase< Rhs > & b ) const [inline]

This method finds a solution x to the equation Ax=b, where A is the matrix of which *this is the QR decomposition.

Parameters:

b	the right-hand-side of the equation to solve.

Returns:: the exact or least-square solution if the rank is greater or equal to the number of columns of A, and an arbitrary solution otherwise.

Note:: The case where b is a matrix is not yet implemented. Also, this code is space inefficient.

Example:

Output:

Definition at line 158 of file FullPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "FullPivHouseholderQR is not initialized.");
      return Solve<FullPivHouseholderQR, Rhs>(*this, b.derived());
    }

template<typename _MatrixType>

RealScalar Eigen::FullPivHouseholderQR< _MatrixType >::threshold ( ) const [inline]

Returns the threshold that will be used by certain methods such as rank().

See the documentation of setThreshold(const RealScalar&).

Definition at line 351 of file FullPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized || m_usePrescribedThreshold);
      return m_usePrescribedThreshold ? m_prescribedThreshold
      // this formula comes from experimenting (see "LU precision tuning" thread on the list)
      // and turns out to be identical to Higham's formula used already in LDLt.
                                      : NumTraits<Scalar>::epsilon() * RealScalar(m_qr.diagonalSize());
    }