Householder rank-revealing QR decomposition of a matrix with column-pivoting. More...

#include <ColPivHouseholderQR.h>

Inheritance diagram for Eigen::ColPivHouseholderQR< _MatrixType >:

Collaboration diagram for Eigen::ColPivHouseholderQR< _MatrixType >:

Public Types
enum	{ RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, Options = MatrixType::Options, MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }
typedef _MatrixType	MatrixType
typedef MatrixType::Scalar	Scalar
typedef MatrixType::RealScalar	RealScalar
typedef MatrixType::StorageIndex	StorageIndex
typedef Matrix< Scalar, RowsAtCompileTime, RowsAtCompileTime, Options, MaxRowsAtCompileTime, MaxRowsAtCompileTime >	MatrixQType
typedef internal::plain_diag_type < MatrixType >::type	HCoeffsType
typedef PermutationMatrix < ColsAtCompileTime, MaxColsAtCompileTime >	PermutationType
typedef internal::plain_row_type < MatrixType, Index >::type	IntRowVectorType
typedef internal::plain_row_type < MatrixType >::type	RowVectorType
typedef internal::plain_row_type < MatrixType, RealScalar > ::type	RealRowVectorType
typedef HouseholderSequence < MatrixType, typename internal::remove_all< typename HCoeffsType::ConjugateReturnType > ::type >	HouseholderSequenceType
typedef MatrixType::PlainObject	PlainObject
Public Member Functions
	ColPivHouseholderQR ()
	Default Constructor.
	ColPivHouseholderQR (Index rows, Index cols)
	Default Constructor with memory preallocation.
template<typename InputType >
	ColPivHouseholderQR (const EigenBase< InputType > &matrix)
	Constructs a QR factorization from a given matrix.
template<typename Rhs >
const Solve < ColPivHouseholderQR, Rhs >	solve (const MatrixBase< Rhs > &b) const
HouseholderSequenceType	householderQ () const
HouseholderSequenceType	matrixQ () const
const MatrixType &	matrixQR () const
const MatrixType &	matrixR () const
template<typename InputType >
ColPivHouseholderQR &	compute (const EigenBase< InputType > &matrix)
const PermutationType &	colsPermutation () const
MatrixType::RealScalar	absDeterminant () const
MatrixType::RealScalar	logAbsDeterminant () const
Index	rank () const
Index	dimensionOfKernel () const
bool	isInjective () const
bool	isSurjective () const
bool	isInvertible () const
const Inverse < ColPivHouseholderQR >	inverse () const
Index	rows () const
Index	cols () const
const HCoeffsType &	hCoeffs () const
ColPivHouseholderQR &	setThreshold (const RealScalar &threshold)
ColPivHouseholderQR &	setThreshold (Default_t)
RealScalar	threshold () const
Index	nonzeroPivots () const
RealScalar	maxPivot () const
ComputationInfo	info () const
	Reports whether the QR factorization was succesful.
template<typename RhsType , typename DstType >
EIGEN_DEVICE_FUNC void	_solve_impl (const RhsType &rhs, DstType &dst) const
Protected Member Functions
void	computeInPlace ()
Static Protected Member Functions
static void	check_template_parameters ()
Protected Attributes
MatrixType	m_qr
HCoeffsType	m_hCoeffs
PermutationType	m_colsPermutation
IntRowVectorType	m_colsTranspositions
RowVectorType	m_temp
RealRowVectorType	m_colNormsUpdated
RealRowVectorType	m_colNormsDirect
bool	m_isInitialized
bool	m_usePrescribedThreshold
RealScalar	m_prescribedThreshold
RealScalar	m_maxpivot
Index	m_nonzero_pivots
Index	m_det_pq
Private Types
typedef PermutationType::StorageIndex	PermIndexType
Friends
class	CompleteOrthogonalDecomposition< MatrixType >

Detailed Description

template<typename _MatrixType>
class Eigen::ColPivHouseholderQR< _MatrixType >

Householder rank-revealing QR decomposition of a matrix with column-pivoting.

Template Parameters:

_MatrixType the type of the matrix of which we are computing the QR decomposition

This class performs a rank-revealing QR decomposition of a matrix A into matrices P, Q and R such that

$\mathbf{A} \, \mathbf{P} = \mathbf{Q} \, \mathbf{R}$

by using Householder transformations. Here, P is a permutation matrix, Q a unitary matrix and R an upper triangular matrix.

This decomposition performs column pivoting in order to be rank-revealing and improve numerical stability. It is slower than HouseholderQR, and faster than FullPivHouseholderQR.

See also:: MatrixBase::colPivHouseholderQr()

Definition at line 46 of file ColPivHouseholderQR.h.

Member Typedef Documentation

template<typename _MatrixType>

typedef internal::plain_diag_type<MatrixType>::type Eigen::ColPivHouseholderQR< _MatrixType >::HCoeffsType

Definition at line 63 of file ColPivHouseholderQR.h.

template<typename _MatrixType>

typedef HouseholderSequence<MatrixType,typename internal::remove_all<typename HCoeffsType::ConjugateReturnType>::type> Eigen::ColPivHouseholderQR< _MatrixType >::HouseholderSequenceType

Definition at line 68 of file ColPivHouseholderQR.h.

template<typename _MatrixType>

typedef internal::plain_row_type<MatrixType, Index>::type Eigen::ColPivHouseholderQR< _MatrixType >::IntRowVectorType

Definition at line 65 of file ColPivHouseholderQR.h.

template<typename _MatrixType>

typedef Matrix<Scalar, RowsAtCompileTime, RowsAtCompileTime, Options, MaxRowsAtCompileTime, MaxRowsAtCompileTime> Eigen::ColPivHouseholderQR< _MatrixType >::MatrixQType

Definition at line 62 of file ColPivHouseholderQR.h.

template<typename _MatrixType>

typedef _MatrixType Eigen::ColPivHouseholderQR< _MatrixType >::MatrixType

Definition at line 50 of file ColPivHouseholderQR.h.

template<typename _MatrixType>

typedef PermutationType::StorageIndex Eigen::ColPivHouseholderQR< _MatrixType >::PermIndexType [private]

Definition at line 73 of file ColPivHouseholderQR.h.

template<typename _MatrixType>

typedef PermutationMatrix<ColsAtCompileTime, MaxColsAtCompileTime> Eigen::ColPivHouseholderQR< _MatrixType >::PermutationType

Definition at line 64 of file ColPivHouseholderQR.h.

template<typename _MatrixType>

typedef MatrixType::PlainObject Eigen::ColPivHouseholderQR< _MatrixType >::PlainObject

Definition at line 69 of file ColPivHouseholderQR.h.

template<typename _MatrixType>

typedef internal::plain_row_type<MatrixType, RealScalar>::type Eigen::ColPivHouseholderQR< _MatrixType >::RealRowVectorType

Definition at line 67 of file ColPivHouseholderQR.h.

template<typename _MatrixType>

typedef MatrixType::RealScalar Eigen::ColPivHouseholderQR< _MatrixType >::RealScalar

Definition at line 59 of file ColPivHouseholderQR.h.

template<typename _MatrixType>

typedef internal::plain_row_type<MatrixType>::type Eigen::ColPivHouseholderQR< _MatrixType >::RowVectorType

Definition at line 66 of file ColPivHouseholderQR.h.

template<typename _MatrixType>

typedef MatrixType::Scalar Eigen::ColPivHouseholderQR< _MatrixType >::Scalar

Definition at line 58 of file ColPivHouseholderQR.h.

template<typename _MatrixType>

typedef MatrixType::StorageIndex Eigen::ColPivHouseholderQR< _MatrixType >::StorageIndex

Definition at line 61 of file ColPivHouseholderQR.h.

Member Enumeration Documentation

template<typename _MatrixType>

anonymous enum

Enumerator:

RowsAtCompileTime
ColsAtCompileTime
Options
MaxRowsAtCompileTime
MaxColsAtCompileTime

Definition at line 51 of file ColPivHouseholderQR.h.

         {
      RowsAtCompileTime = MatrixType::RowsAtCompileTime,
      ColsAtCompileTime = MatrixType::ColsAtCompileTime,
      Options = MatrixType::Options,
      MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime,
      MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime
    };

Constructor & Destructor Documentation

template<typename _MatrixType>

Eigen::ColPivHouseholderQR< _MatrixType >::ColPivHouseholderQR ( ) [inline]

Default Constructor.

The default constructor is useful in cases in which the user intends to perform decompositions via ColPivHouseholderQR::compute(const MatrixType&).

Definition at line 83 of file ColPivHouseholderQR.h.

      : m_qr(),
        m_hCoeffs(),
        m_colsPermutation(),
        m_colsTranspositions(),
        m_temp(),
        m_colNormsUpdated(),
        m_colNormsDirect(),
        m_isInitialized(false),
        m_usePrescribedThreshold(false) {}

template<typename _MatrixType>

Eigen::ColPivHouseholderQR< _MatrixType >::ColPivHouseholderQR	(	Index	rows,
		Index	cols
	)		`[inline]`

Default Constructor with memory preallocation.

Like the default constructor but with preallocation of the internal data according to the specified problem size.

See also:: ColPivHouseholderQR()

Definition at line 100 of file ColPivHouseholderQR.h.

      : m_qr(rows, cols),
        m_hCoeffs((std::min)(rows,cols)),
        m_colsPermutation(PermIndexType(cols)),
        m_colsTranspositions(cols),
        m_temp(cols),
        m_colNormsUpdated(cols),
        m_colNormsDirect(cols),
        m_isInitialized(false),
        m_usePrescribedThreshold(false) {}

template<typename _MatrixType>

template<typename InputType >

Eigen::ColPivHouseholderQR< _MatrixType >::ColPivHouseholderQR ( const EigenBase< InputType > & matrix ) [inline, explicit]

Constructs a QR factorization from a given matrix.

This constructor computes the QR factorization of the matrix matrix by calling the method compute(). It is a short cut for:

 ColPivHouseholderQR<MatrixType> qr(matrix.rows(), matrix.cols());
 qr.compute(matrix);

See also:: compute()

Definition at line 124 of file ColPivHouseholderQR.h.

      : m_qr(matrix.rows(), matrix.cols()),
        m_hCoeffs((std::min)(matrix.rows(),matrix.cols())),
        m_colsPermutation(PermIndexType(matrix.cols())),
        m_colsTranspositions(matrix.cols()),
        m_temp(matrix.cols()),
        m_colNormsUpdated(matrix.cols()),
        m_colNormsDirect(matrix.cols()),
        m_isInitialized(false),
        m_usePrescribedThreshold(false)
    {
      compute(matrix.derived());
    }

Member Function Documentation

template<typename _MatrixType >

template<typename RhsType , typename DstType >

void Eigen::ColPivHouseholderQR< _MatrixType >::_solve_impl	(	const RhsType &	rhs,
		DstType &	dst
	)		const

Definition at line 569 of file ColPivHouseholderQR.h.

{
  eigen_assert(rhs.rows() == rows());

  const Index nonzero_pivots = nonzeroPivots();

  if(nonzero_pivots == 0)
  {
    dst.setZero();
    return;
  }

  typename RhsType::PlainObject c(rhs);

  // Note that the matrix Q = H_0^* H_1^*... so its inverse is Q^* = (H_0 H_1 ...)^T
  c.applyOnTheLeft(householderSequence(m_qr, m_hCoeffs)
                    .setLength(nonzero_pivots)
                    .transpose()
    );

  m_qr.topLeftCorner(nonzero_pivots, nonzero_pivots)
      .template triangularView<Upper>()
      .solveInPlace(c.topRows(nonzero_pivots));

  for(Index i = 0; i < nonzero_pivots; ++i) dst.row(m_colsPermutation.indices().coeff(i)) = c.row(i);
  for(Index i = nonzero_pivots; i < cols(); ++i) dst.row(m_colsPermutation.indices().coeff(i)).setZero();
}

template<typename MatrixType >

MatrixType::RealScalar Eigen::ColPivHouseholderQR< MatrixType >::absDeterminant ( ) const

Returns:: the absolute value of the determinant of the matrix of which *this is the QR decomposition. It has only linear complexity (that is, O(n) where n is the dimension of the square matrix) as the QR decomposition has already been computed.

Note:: This is only for square matrices.

Warning:: a determinant can be very big or small, so for matrices of large enough dimension, there is a risk of overflow/underflow. One way to work around that is to use logAbsDeterminant() instead.

See also:: logAbsDeterminant(), MatrixBase::determinant()

Definition at line 430 of file ColPivHouseholderQR.h.

{
  using std::abs;
  eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
  eigen_assert(m_qr.rows() == m_qr.cols() && "You can't take the determinant of a non-square matrix!");
  return abs(m_qr.diagonal().prod());
}

template<typename _MatrixType>

static void Eigen::ColPivHouseholderQR< _MatrixType >::check_template_parameters ( ) [inline, static, protected]

Definition at line 409 of file ColPivHouseholderQR.h.

    {
      EIGEN_STATIC_ASSERT_NON_INTEGER(Scalar);
    }

template<typename _MatrixType>

Index Eigen::ColPivHouseholderQR< _MatrixType >::cols ( void ) const [inline]

Definition at line 310 of file ColPivHouseholderQR.h.

{ return m_qr.cols(); }

template<typename _MatrixType>

const PermutationType& Eigen::ColPivHouseholderQR< _MatrixType >::colsPermutation ( ) const [inline]

Returns:: a const reference to the column permutation matrix

Definition at line 196 of file ColPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
      return m_colsPermutation;
    }

template<typename MatrixType >

template<typename InputType >

ColPivHouseholderQR< MatrixType > & Eigen::ColPivHouseholderQR< MatrixType >::compute ( const EigenBase< InputType > & matrix )

Performs the QR factorization of the given matrix matrix. The result of the factorization is stored into *this, and a reference to *this is returned.

See also:: class ColPivHouseholderQR, ColPivHouseholderQR(const MatrixType&)

Definition at line 454 of file ColPivHouseholderQR.h.

{
  check_template_parameters();

  // the column permutation is stored as int indices, so just to be sure:
  eigen_assert(matrix.cols()<=NumTraits<int>::highest());

  m_qr = matrix;

  computeInPlace();

  return *this;
}

template<typename MatrixType >

void Eigen::ColPivHouseholderQR< MatrixType >::computeInPlace ( ) [protected]

Definition at line 469 of file ColPivHouseholderQR.h.

{
  using std::abs;

  Index rows = m_qr.rows();
  Index cols = m_qr.cols();
  Index size = m_qr.diagonalSize();

  m_hCoeffs.resize(size);

  m_temp.resize(cols);

  m_colsTranspositions.resize(m_qr.cols());
  Index number_of_transpositions = 0;

  m_colNormsUpdated.resize(cols);
  m_colNormsDirect.resize(cols);
  for (Index k = 0; k < cols; ++k) {
    // colNormsDirect(k) caches the most recent directly computed norm of
    // column k.
    m_colNormsDirect.coeffRef(k) = m_qr.col(k).norm();
    m_colNormsUpdated.coeffRef(k) = m_colNormsDirect.coeffRef(k);
  }

  RealScalar threshold_helper =  numext::abs2(m_colNormsUpdated.maxCoeff() * NumTraits<Scalar>::epsilon()) / RealScalar(rows);
  RealScalar norm_downdate_threshold = numext::sqrt(NumTraits<Scalar>::epsilon());

  m_nonzero_pivots = size; // the generic case is that in which all pivots are nonzero (invertible case)
  m_maxpivot = RealScalar(0);

  for(Index k = 0; k < size; ++k)
  {
    // first, we look up in our table m_colNormsUpdated which column has the biggest norm
    Index biggest_col_index;
    RealScalar biggest_col_sq_norm = numext::abs2(m_colNormsUpdated.tail(cols-k).maxCoeff(&biggest_col_index));
    biggest_col_index += k;

    // Track the number of meaningful pivots but do not stop the decomposition to make
    // sure that the initial matrix is properly reproduced. See bug 941.
    if(m_nonzero_pivots==size && biggest_col_sq_norm < threshold_helper * RealScalar(rows-k))
      m_nonzero_pivots = k;

    // apply the transposition to the columns
    m_colsTranspositions.coeffRef(k) = biggest_col_index;
    if(k != biggest_col_index) {
      m_qr.col(k).swap(m_qr.col(biggest_col_index));
      std::swap(m_colNormsUpdated.coeffRef(k), m_colNormsUpdated.coeffRef(biggest_col_index));
      std::swap(m_colNormsDirect.coeffRef(k), m_colNormsDirect.coeffRef(biggest_col_index));
      ++number_of_transpositions;
    }

    // generate the householder vector, store it below the diagonal
    RealScalar beta;
    m_qr.col(k).tail(rows-k).makeHouseholderInPlace(m_hCoeffs.coeffRef(k), beta);

    // apply the householder transformation to the diagonal coefficient
    m_qr.coeffRef(k,k) = beta;

    // remember the maximum absolute value of diagonal coefficients
    if(abs(beta) > m_maxpivot) m_maxpivot = abs(beta);

    // apply the householder transformation
    m_qr.bottomRightCorner(rows-k, cols-k-1)
        .applyHouseholderOnTheLeft(m_qr.col(k).tail(rows-k-1), m_hCoeffs.coeffRef(k), &m_temp.coeffRef(k+1));

    // update our table of norms of the columns
    for (Index j = k + 1; j < cols; ++j) {
      // The following implements the stable norm downgrade step discussed in
      // http://www.netlib.org/lapack/lawnspdf/lawn176.pdf
      // and used in LAPACK routines xGEQPF and xGEQP3.
      // See lines 278-297 in http://www.netlib.org/lapack/explore-html/dc/df4/sgeqpf_8f_source.html
      if (m_colNormsUpdated.coeffRef(j) != 0) {
        RealScalar temp = abs(m_qr.coeffRef(k, j)) / m_colNormsUpdated.coeffRef(j);
        temp = (RealScalar(1) + temp) * (RealScalar(1) - temp);
        temp = temp < 0 ? 0 : temp;
        RealScalar temp2 = temp * numext::abs2(m_colNormsUpdated.coeffRef(j) /
                                               m_colNormsDirect.coeffRef(j));
        if (temp2 <= norm_downdate_threshold) {
          // The updated norm has become too inaccurate so re-compute the column
          // norm directly.
          m_colNormsDirect.coeffRef(j) = m_qr.col(j).tail(rows - k - 1).norm();
          m_colNormsUpdated.coeffRef(j) = m_colNormsDirect.coeffRef(j);
        } else {
          m_colNormsUpdated.coeffRef(j) *= numext::sqrt(temp);
        }
      }
    }
  }

  m_colsPermutation.setIdentity(PermIndexType(cols));
  for(PermIndexType k = 0; k < size/*m_nonzero_pivots*/; ++k)
    m_colsPermutation.applyTranspositionOnTheRight(k, PermIndexType(m_colsTranspositions.coeff(k)));

  m_det_pq = (number_of_transpositions%2) ? -1 : 1;
  m_isInitialized = true;
}

template<typename _MatrixType>

Index Eigen::ColPivHouseholderQR< _MatrixType >::dimensionOfKernel ( ) const [inline]

Returns:: the dimension of the kernel of the matrix of which *this is the QR decomposition.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 254 of file ColPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
      return cols() - rank();
    }

template<typename _MatrixType>

const HCoeffsType& Eigen::ColPivHouseholderQR< _MatrixType >::hCoeffs ( ) const [inline]

Returns:: a const reference to the vector of Householder coefficients used to represent the factor Q.

For advanced uses only.

Definition at line 316 of file ColPivHouseholderQR.h.

{ return m_hCoeffs; }

template<typename MatrixType >

ColPivHouseholderQR< MatrixType >::HouseholderSequenceType Eigen::ColPivHouseholderQR< MatrixType >::householderQ ( ) const

Returns:

the matrix Q as a sequence of householder transformations. You can extract the meaningful part only by using:

 qr.householderQ().setLength(qr.nonzeroPivots())

Definition at line 618 of file ColPivHouseholderQR.h.

{
  eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
  return HouseholderSequenceType(m_qr, m_hCoeffs.conjugate());
}

template<typename _MatrixType>

ComputationInfo Eigen::ColPivHouseholderQR< _MatrixType >::info ( ) const [inline]

Reports whether the QR factorization was succesful.

Note:: This function always returns Success. It is provided for compatibility with other factorization routines.

Returns:: Success

Definition at line 393 of file ColPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "Decomposition is not initialized.");
      return Success;
    }

template<typename _MatrixType>

const Inverse<ColPivHouseholderQR> Eigen::ColPivHouseholderQR< _MatrixType >::inverse ( ) const [inline]

Returns:: the inverse of the matrix of which *this is the QR decomposition.

Note:: If this matrix is not invertible, the returned matrix has undefined coefficients. Use isInvertible() to first determine whether this matrix is invertible.

Definition at line 303 of file ColPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
      return Inverse<ColPivHouseholderQR>(*this);
    }

template<typename _MatrixType>

bool Eigen::ColPivHouseholderQR< _MatrixType >::isInjective ( ) const [inline]

Returns:: true if the matrix of which *this is the QR decomposition represents an injective linear map, i.e. has trivial kernel; false otherwise.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 267 of file ColPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
      return rank() == cols();
    }

template<typename _MatrixType>

bool Eigen::ColPivHouseholderQR< _MatrixType >::isInvertible ( ) const [inline]

Returns:: true if the matrix of which *this is the QR decomposition is invertible.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 292 of file ColPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
      return isInjective() && isSurjective();
    }

template<typename _MatrixType>

bool Eigen::ColPivHouseholderQR< _MatrixType >::isSurjective ( ) const [inline]

Returns:: true if the matrix of which *this is the QR decomposition represents a surjective linear map; false otherwise.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 280 of file ColPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
      return rank() == rows();
    }

template<typename MatrixType >

MatrixType::RealScalar Eigen::ColPivHouseholderQR< MatrixType >::logAbsDeterminant ( ) const

Returns:: the natural log of the absolute value of the determinant of the matrix of which *this is the QR decomposition. It has only linear complexity (that is, O(n) where n is the dimension of the square matrix) as the QR decomposition has already been computed.

Note:: This is only for square matrices.; This method is useful to work around the risk of overflow/underflow that's inherent to determinant computation.

See also:: absDeterminant(), MatrixBase::determinant()

Definition at line 439 of file ColPivHouseholderQR.h.

{
  eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
  eigen_assert(m_qr.rows() == m_qr.cols() && "You can't take the determinant of a non-square matrix!");
  return m_qr.diagonal().cwiseAbs().array().log().sum();
}

template<typename _MatrixType>

HouseholderSequenceType Eigen::ColPivHouseholderQR< _MatrixType >::matrixQ ( ) const [inline]

Definition at line 164 of file ColPivHouseholderQR.h.

    {
      return householderQ();
    }

template<typename _MatrixType>

const MatrixType& Eigen::ColPivHouseholderQR< _MatrixType >::matrixQR ( ) const [inline]

Returns:: a reference to the matrix where the Householder QR decomposition is stored

Definition at line 171 of file ColPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
      return m_qr;
    }

template<typename _MatrixType>

const MatrixType& Eigen::ColPivHouseholderQR< _MatrixType >::matrixR ( ) const [inline]

Returns:: a reference to the matrix where the result Householder QR is stored

Warning:

The strict lower part of this matrix contains internal values. Only the upper triangular part should be referenced. To get it, use

 matrixR().template triangularView<Upper>()

For rank-deficient matrices, use

 matrixR().topLeftCorner(rank(), rank()).template triangularView<Upper>()

Definition at line 186 of file ColPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
      return m_qr;
    }

template<typename _MatrixType>

RealScalar Eigen::ColPivHouseholderQR< _MatrixType >::maxPivot ( ) const [inline]

Returns:: the absolute value of the biggest pivot, i.e. the biggest diagonal coefficient of R.

Definition at line 385 of file ColPivHouseholderQR.h.

{ return m_maxpivot; }

template<typename _MatrixType>

Index Eigen::ColPivHouseholderQR< _MatrixType >::nonzeroPivots ( ) const [inline]

Returns:: the number of nonzero pivots in the QR decomposition. Here nonzero is meant in the exact sense, not in a fuzzy sense. So that notion isn't really intrinsically interesting, but it is still useful when implementing algorithms.

See also:: rank()

Definition at line 376 of file ColPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
      return m_nonzero_pivots;
    }

template<typename _MatrixType>

Index Eigen::ColPivHouseholderQR< _MatrixType >::rank ( ) const [inline]

Returns:: the rank of the matrix of which *this is the QR decomposition.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 237 of file ColPivHouseholderQR.h.

    {
      using std::abs;
      eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
      RealScalar premultiplied_threshold = abs(m_maxpivot) * threshold();
      Index result = 0;
      for(Index i = 0; i < m_nonzero_pivots; ++i)
        result += (abs(m_qr.coeff(i,i)) > premultiplied_threshold);
      return result;
    }

template<typename _MatrixType>

Index Eigen::ColPivHouseholderQR< _MatrixType >::rows ( void ) const [inline]

Definition at line 309 of file ColPivHouseholderQR.h.

{ return m_qr.rows(); }

template<typename _MatrixType>

ColPivHouseholderQR& Eigen::ColPivHouseholderQR< _MatrixType >::setThreshold ( const RealScalar & threshold ) [inline]

Allows to prescribe a threshold to be used by certain methods, such as rank(), who need to determine when pivots are to be considered nonzero. This is not used for the QR decomposition itself.

When it needs to get the threshold value, Eigen calls threshold(). By default, this uses a formula to automatically determine a reasonable threshold. Once you have called the present method setThreshold(const RealScalar&), your value is used instead.

Parameters:

threshold The new value to use as the threshold.

A pivot will be considered nonzero if its absolute value is strictly greater than 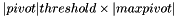$\vert pivot \vert \leqslant threshold \times \vert maxpivot \vert$ where maxpivot is the biggest pivot.

If you want to come back to the default behavior, call setThreshold(Default_t)

Definition at line 335 of file ColPivHouseholderQR.h.

    {
      m_usePrescribedThreshold = true;
      m_prescribedThreshold = threshold;
      return *this;
    }

template<typename _MatrixType>

ColPivHouseholderQR& Eigen::ColPivHouseholderQR< _MatrixType >::setThreshold ( Default_t ) [inline]

Allows to come back to the default behavior, letting Eigen use its default formula for determining the threshold.

You should pass the special object Eigen::Default as parameter here.

 qr.setThreshold(Eigen::Default);

See the documentation of setThreshold(const RealScalar&).

Definition at line 350 of file ColPivHouseholderQR.h.

    {
      m_usePrescribedThreshold = false;
      return *this;
    }

template<typename _MatrixType>

template<typename Rhs >

const Solve<ColPivHouseholderQR, Rhs> Eigen::ColPivHouseholderQR< _MatrixType >::solve ( const MatrixBase< Rhs > & b ) const [inline]

This method finds a solution x to the equation Ax=b, where A is the matrix of which *this is the QR decomposition, if any exists.

Parameters:

b	the right-hand-side of the equation to solve.

Returns:: a solution.

Note:: The case where b is a matrix is not yet implemented. Also, this code is space inefficient.

Example:

Output:

Definition at line 157 of file ColPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized && "ColPivHouseholderQR is not initialized.");
      return Solve<ColPivHouseholderQR, Rhs>(*this, b.derived());
    }

template<typename _MatrixType>

RealScalar Eigen::ColPivHouseholderQR< _MatrixType >::threshold ( ) const [inline]

Returns the threshold that will be used by certain methods such as rank().

See the documentation of setThreshold(const RealScalar&).

Definition at line 360 of file ColPivHouseholderQR.h.

    {
      eigen_assert(m_isInitialized || m_usePrescribedThreshold);
      return m_usePrescribedThreshold ? m_prescribedThreshold
      // this formula comes from experimenting (see "LU precision tuning" thread on the list)
      // and turns out to be identical to Higham's formula used already in LDLt.
                                      : NumTraits<Scalar>::epsilon() * RealScalar(m_qr.diagonalSize());
    }