MOAB  4.9.3pre
Public Types | Public Member Functions | Protected Member Functions | Protected Attributes | Private Types | Friends
Eigen::HouseholderSequence< VectorsType, CoeffsType, Side > Class Template Reference

Sequence of Householder reflections acting on subspaces with decreasing size. More...

#include <HouseholderSequence.h>

Inheritance diagram for Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >:
Inheritance graph
[legend]
Collaboration diagram for Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >:
Collaboration graph
[legend]

List of all members.

Public Types

enum  { RowsAtCompileTime = internal::traits<HouseholderSequence>::RowsAtCompileTime, ColsAtCompileTime = internal::traits<HouseholderSequence>::ColsAtCompileTime, MaxRowsAtCompileTime = internal::traits<HouseholderSequence>::MaxRowsAtCompileTime, MaxColsAtCompileTime = internal::traits<HouseholderSequence>::MaxColsAtCompileTime }
typedef internal::traits
< HouseholderSequence >
::Scalar 		Scalar
typedef HouseholderSequence
< typename
internal::conditional
< NumTraits< Scalar >
::IsComplex, typename
internal::remove_all< typename
VectorsType::ConjugateReturnType >
::type, VectorsType >::type,
typename internal::conditional
< NumTraits< Scalar >
::IsComplex, typename
internal::remove_all< typename
CoeffsType::ConjugateReturnType >
::type, CoeffsType >::type,
Side > 		ConjugateReturnType

Public Member Functions

 HouseholderSequence (const VectorsType &v, const CoeffsType &h)
 Constructor.
 HouseholderSequence (const HouseholderSequence &other)
 Copy constructor.
Index rows () const
 Number of rows of transformation viewed as a matrix.
Index cols () const
 Number of columns of transformation viewed as a matrix.
const EssentialVectorType essentialVector (Index k) const
 Essential part of a Householder vector.
HouseholderSequence transpose () const
 Transpose of the Householder sequence.
ConjugateReturnType conjugate () const
 Complex conjugate of the Householder sequence.
ConjugateReturnType adjoint () const
 Adjoint (conjugate transpose) of the Householder sequence.
ConjugateReturnType inverse () const
 Inverse of the Householder sequence (equals the adjoint).
template<typename DestType >
void evalTo (DestType &dst) const
template<typename Dest , typename Workspace >
void evalTo (Dest &dst, Workspace &workspace) const
template<typename Dest >
void applyThisOnTheRight (Dest &dst) const
template<typename Dest , typename Workspace >
void applyThisOnTheRight (Dest &dst, Workspace &workspace) const
template<typename Dest >
void applyThisOnTheLeft (Dest &dst) const
template<typename Dest , typename Workspace >
void applyThisOnTheLeft (Dest &dst, Workspace &workspace) const
template<typename OtherDerived >
internal::matrix_type_times_scalar_type
< Scalar, OtherDerived >::Type 		operator* (const MatrixBase< OtherDerived > &other) const
 Computes the product of a Householder sequence with a matrix.
HouseholderSequence & setLength (Index length)
 Sets the length of the Householder sequence.
HouseholderSequence & setShift (Index shift)
 Sets the shift of the Householder sequence.
Index length () const
 Returns the length of the Householder sequence.
Index shift () const
 Returns the shift of the Householder sequence.

Protected Member Functions

HouseholderSequence & setTrans (bool trans)
 Sets the transpose flag.
bool trans () const
 Returns the transpose flag.

Protected Attributes

VectorsType::Nested m_vectors
CoeffsType::Nested m_coeffs
bool m_trans
Index m_length
Index m_shift

Private Types

typedef
internal::hseq_side_dependent_impl
< VectorsType, CoeffsType,
Side >::EssentialVectorType 		EssentialVectorType

Friends

struct internal::hseq_side_dependent_impl
class HouseholderSequence

Detailed Description

template<typename VectorsType, typename CoeffsType, int Side>
class Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >

Sequence of Householder reflections acting on subspaces with decreasing size.

Template Parameters:
VectorsTypetype of matrix containing the Householder vectors
CoeffsTypetype of vector containing the Householder coefficients
Sideeither OnTheLeft (the default) or OnTheRight

This class represents a product sequence of Householder reflections where the first Householder reflection acts on the whole space, the second Householder reflection leaves the one-dimensional subspace spanned by the first unit vector invariant, the third Householder reflection leaves the two-dimensional subspace spanned by the first two unit vectors invariant, and so on up to the last reflection which leaves all but one dimensions invariant and acts only on the last dimension. Such sequences of Householder reflections are used in several algorithms to zero out certain parts of a matrix. Indeed, the methods HessenbergDecomposition::matrixQ(), Tridiagonalization::matrixQ(), HouseholderQR::householderQ(), and ColPivHouseholderQR::householderQ() all return a HouseholderSequence.

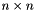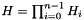More precisely, the class HouseholderSequence represents an $ n \times n $ matrix $ H $ of the form $ H = \prod_{i=0}^{n-1} H_i $ where the i-th Householder reflection is 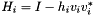$ H_i = I - h_i v_i v_i^* $. The i-th Householder coefficient 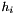$ h_i $ is a scalar and the i-th Householder vector $ v_i $ is a vector of the form

\[ v_i = [\underbrace{0, \ldots, 0}_{i-1\mbox{ zeros}}, 1, \underbrace{*, \ldots,*}_{n-i\mbox{ arbitrary entries}} ]. \]

The last $ n-i $ entries of $ v_i $ are called the essential part of the Householder vector.

Typical usages are listed below, where H is a HouseholderSequence: 

 A.applyOnTheRight(H);             // A = A * H
 A.applyOnTheLeft(H);              // A = H * A
 A.applyOnTheRight(H.adjoint());   // A = A * H^*
 A.applyOnTheLeft(H.adjoint());    // A = H^* * A
 MatrixXd Q = H;                   // conversion to a dense matrix

In addition to the adjoint, you can also apply the inverse (=adjoint), the transpose, and the conjugate operators.

See the documentation for HouseholderSequence(const VectorsType&, const CoeffsType&) for an example.

See also:
MatrixBase::applyOnTheLeft(), MatrixBase::applyOnTheRight()

Definition at line 119 of file HouseholderSequence.h.

Member Typedef Documentation

template<typename VectorsType, typename CoeffsType, int Side>
typedef HouseholderSequence< typename internal::conditional<NumTraits<Scalar>::IsComplex, typename internal::remove_all<typename VectorsType::ConjugateReturnType>::type, VectorsType>::type, typename internal::conditional<NumTraits<Scalar>::IsComplex, typename internal::remove_all<typename CoeffsType::ConjugateReturnType>::type, CoeffsType>::type, Side > Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::ConjugateReturnType

Definition at line 141 of file HouseholderSequence.h.

template<typename VectorsType, typename CoeffsType, int Side>
typedef internal::hseq_side_dependent_impl<VectorsType,CoeffsType,Side>::EssentialVectorType Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::EssentialVectorType [private]

Definition at line 122 of file HouseholderSequence.h.

template<typename VectorsType, typename CoeffsType, int Side>
typedef internal::traits<HouseholderSequence>::Scalar Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::Scalar

Definition at line 131 of file HouseholderSequence.h.

Member Enumeration Documentation

template<typename VectorsType, typename CoeffsType, int Side>
anonymous enum
Enumerator:
RowsAtCompileTime 
ColsAtCompileTime 
MaxRowsAtCompileTime 
MaxColsAtCompileTime 

Definition at line 125 of file HouseholderSequence.h.

         {
      RowsAtCompileTime = internal::traits<HouseholderSequence>::RowsAtCompileTime,
      ColsAtCompileTime = internal::traits<HouseholderSequence>::ColsAtCompileTime,
      MaxRowsAtCompileTime = internal::traits<HouseholderSequence>::MaxRowsAtCompileTime,
      MaxColsAtCompileTime = internal::traits<HouseholderSequence>::MaxColsAtCompileTime
    };

Constructor & Destructor Documentation

template<typename VectorsType, typename CoeffsType, int Side>
Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::HouseholderSequence ( const VectorsType &  v,
const CoeffsType &  h 
) [inline]

Constructor.

Parameters:
[in]vMatrix containing the essential parts of the Householder vectors
[in]hVector containing the Householder coefficients

Constructs the Householder sequence with coefficients given by h and vectors given by v. The i-th Householder coefficient 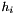$ h_i $ is given by h(i) and the essential part of the i-th Householder vector $ v_i $ is given by v(k,i) with k > i (the subdiagonal part of the i-th column). If v has fewer columns than rows, then the Householder sequence contains as many Householder reflections as there are columns.

Note:
The HouseholderSequence object stores v and h by reference.

Example: 

 Output: 


See also:
setLength(), setShift() 



Definition at line 160 of file HouseholderSequence.h.


      : m_vectors(v), m_coeffs(h), m_trans(false), m_length(v.diagonalSize()),
        m_shift(0)
    {
    }













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::HouseholderSequence 
          (
          const HouseholderSequence< VectorsType, CoeffsType, Side > & 
          other)
           [inline]
        

      







Copy constructor. 



Definition at line 167 of file HouseholderSequence.h.


      : m_vectors(other.m_vectors),
        m_coeffs(other.m_coeffs),
        m_trans(other.m_trans),
        m_length(other.m_length),
        m_shift(other.m_shift)
    {
    }







Member Function Documentation








template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          ConjugateReturnType Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::adjoint 
          (
          )
           const [inline]
        

      







Adjoint (conjugate transpose) of the Householder sequence. 



Definition at line 224 of file HouseholderSequence.h.


    {
      return conjugate().setTrans(!m_trans);
    }













template<typename VectorsType, typename CoeffsType, int Side> 



template<typename Dest > 

      

        

          void Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::applyThisOnTheLeft 
          (
          Dest & 
          dst)
           const [inline]
        

      







Reimplemented from Eigen::EigenBase< HouseholderSequence< VectorsType, CoeffsType, Side > >.



Definition at line 306 of file HouseholderSequence.h.


    {
      Matrix<Scalar,1,Dest::ColsAtCompileTime,RowMajor,1,Dest::MaxColsAtCompileTime> workspace(dst.cols());
      applyThisOnTheLeft(dst, workspace);
    }













template<typename VectorsType, typename CoeffsType, int Side> 



template<typename Dest , typename Workspace > 

      

        

          void Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::applyThisOnTheLeft 
          (
          Dest & 
          dst, 
        

        

          
          
          Workspace & 
          workspace 
        

        

          
          )
           const [inline]
        

      







Definition at line 314 of file HouseholderSequence.h.


    {
      const Index BlockSize = 48;
      // if the entries are large enough, then apply the reflectors by block
      if(m_length>=BlockSize && dst.cols()>1)
      {
        for(Index i = 0; i < m_length; i+=BlockSize)
        {
          Index end = m_trans ? (std::min)(m_length,i+BlockSize) : m_length-i;
          Index k = m_trans ? i : (std::max)(Index(0),end-BlockSize);
          Index bs = end-k;
          Index start = k + m_shift;
          
          typedef Block<typename internal::remove_all<VectorsType>::type,Dynamic,Dynamic> SubVectorsType;
          SubVectorsType sub_vecs1(m_vectors.const_cast_derived(), Side==OnTheRight ? k : start,
                                                                   Side==OnTheRight ? start : k,
                                                                   Side==OnTheRight ? bs : m_vectors.rows()-start,
                                                                   Side==OnTheRight ? m_vectors.cols()-start : bs);
          typename internal::conditional<Side==OnTheRight, Transpose<SubVectorsType>, SubVectorsType&>::type sub_vecs(sub_vecs1);
          Block<Dest,Dynamic,Dynamic> sub_dst(dst,dst.rows()-rows()+m_shift+k,0, rows()-m_shift-k,dst.cols());
          apply_block_householder_on_the_left(sub_dst, sub_vecs, m_coeffs.segment(k, bs), !m_trans);
        }
      }
      else
      {
        workspace.resize(dst.cols());
        for(Index k = 0; k < m_length; ++k)
        {
          Index actual_k = m_trans ? k : m_length-k-1;
          dst.bottomRows(rows()-m_shift-actual_k)
            .applyHouseholderOnTheLeft(essentialVector(actual_k), m_coeffs.coeff(actual_k), workspace.data());
        }
      }
    }













template<typename VectorsType, typename CoeffsType, int Side> 



template<typename Dest > 

      

        

          void Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::applyThisOnTheRight 
          (
          Dest & 
          dst)
           const [inline]
        

      







Reimplemented from Eigen::EigenBase< HouseholderSequence< VectorsType, CoeffsType, Side > >.



Definition at line 286 of file HouseholderSequence.h.


    {
      Matrix<Scalar,1,Dest::RowsAtCompileTime,RowMajor,1,Dest::MaxRowsAtCompileTime> workspace(dst.rows());
      applyThisOnTheRight(dst, workspace);
    }













template<typename VectorsType, typename CoeffsType, int Side> 



template<typename Dest , typename Workspace > 

      

        

          void Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::applyThisOnTheRight 
          (
          Dest & 
          dst, 
        

        

          
          
          Workspace & 
          workspace 
        

        

          
          )
           const [inline]
        

      







Definition at line 294 of file HouseholderSequence.h.


    {
      workspace.resize(dst.rows());
      for(Index k = 0; k < m_length; ++k)
      {
        Index actual_k = m_trans ? m_length-k-1 : k;
        dst.rightCols(rows()-m_shift-actual_k)
           .applyHouseholderOnTheRight(essentialVector(actual_k), m_coeffs.coeff(actual_k), workspace.data());
      }
    }













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          Index Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::cols 
          (
          void 
          )
           const [inline]
        

      







Number of columns of transformation viewed as a matrix. 


Returns:
Number of columns


This equals the dimension of the space that the transformation acts on. 



Reimplemented from Eigen::EigenBase< HouseholderSequence< VectorsType, CoeffsType, Side > >.



Definition at line 186 of file HouseholderSequence.h.


{ return rows(); }













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          ConjugateReturnType Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::conjugate 
          (
          )
           const [inline]
        

      







Complex conjugate of the Householder sequence. 



Definition at line 215 of file HouseholderSequence.h.


    {
      return ConjugateReturnType(m_vectors.conjugate(), m_coeffs.conjugate())
             .setTrans(m_trans)
             .setLength(m_length)
             .setShift(m_shift);
    }













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          const EssentialVectorType Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::essentialVector 
          (
          Index 
          k)
           const [inline]
        

      







Essential part of a Householder vector. 


Parameters:

  

    
[in]kIndex of Householder reflection 

  

  




Returns:
Vector containing non-trivial entries of k-th Householder vector


This function returns the essential part of the Householder vector $ v_i $. This is a vector of length $ n-i $ containing the last $ n-i $ entries of the vector 



\[ v_i = [\underbrace{0, \ldots, 0}_{i-1\mbox{ zeros}}, 1, \underbrace{*, \ldots,*}_{n-i\mbox{ arbitrary entries}} ]. \]



 The index $ i $ equals k + shift(), corresponding to the k-th column of the matrix v passed to the constructor.


See also:
setShift(), shift() 



Definition at line 202 of file HouseholderSequence.h.


    {
      eigen_assert(k >= 0 && k < m_length);
      return internal::hseq_side_dependent_impl<VectorsType,CoeffsType,Side>::essentialVector(*this, k);
    }













template<typename VectorsType, typename CoeffsType, int Side> 



template<typename DestType > 

      

        

          void Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::evalTo 
          (
          DestType & 
          dst)
           const [inline]
        

      







Definition at line 233 of file HouseholderSequence.h.


    {
      Matrix<Scalar, DestType::RowsAtCompileTime, 1,
             AutoAlign|ColMajor, DestType::MaxRowsAtCompileTime, 1> workspace(rows());
      evalTo(dst, workspace);
    }













template<typename VectorsType, typename CoeffsType, int Side> 



template<typename Dest , typename Workspace > 

      

        

          void Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::evalTo 
          (
          Dest & 
          dst, 
        

        

          
          
          Workspace & 
          workspace 
        

        

          
          )
           const [inline]
        

      







Definition at line 242 of file HouseholderSequence.h.


    {
      workspace.resize(rows());
      Index vecs = m_length;
      if(    internal::is_same<typename internal::remove_all<VectorsType>::type,Dest>::value
          && internal::extract_data(dst) == internal::extract_data(m_vectors))
      {
        // in-place
        dst.diagonal().setOnes();
        dst.template triangularView<StrictlyUpper>().setZero();
        for(Index k = vecs-1; k >= 0; --k)
        {
          Index cornerSize = rows() - k - m_shift;
          if(m_trans)
            dst.bottomRightCorner(cornerSize, cornerSize)
               .applyHouseholderOnTheRight(essentialVector(k), m_coeffs.coeff(k), workspace.data());
          else
            dst.bottomRightCorner(cornerSize, cornerSize)
               .applyHouseholderOnTheLeft(essentialVector(k), m_coeffs.coeff(k), workspace.data());

          // clear the off diagonal vector
          dst.col(k).tail(rows()-k-1).setZero();
        }
        // clear the remaining columns if needed
        for(Index k = 0; k<cols()-vecs ; ++k)
          dst.col(k).tail(rows()-k-1).setZero();
      }
      else
      {
        dst.setIdentity(rows(), rows());
        for(Index k = vecs-1; k >= 0; --k)
        {
          Index cornerSize = rows() - k - m_shift;
          if(m_trans)
            dst.bottomRightCorner(cornerSize, cornerSize)
               .applyHouseholderOnTheRight(essentialVector(k), m_coeffs.coeff(k), &workspace.coeffRef(0));
          else
            dst.bottomRightCorner(cornerSize, cornerSize)
               .applyHouseholderOnTheLeft(essentialVector(k), m_coeffs.coeff(k), &workspace.coeffRef(0));
        }
      }
    }













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          ConjugateReturnType Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::inverse 
          (
          )
           const [inline]
        

      







Inverse of the Householder sequence (equals the adjoint). 



Definition at line 230 of file HouseholderSequence.h.


{ return adjoint(); }













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          Index Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::length 
          (
          )
           const [inline]
        

      







Returns the length of the Householder sequence. 



Definition at line 399 of file HouseholderSequence.h.













template<typename VectorsType, typename CoeffsType, int Side> 



template<typename OtherDerived > 

      

        

          internal::matrix_type_times_scalar_type<Scalar, OtherDerived>::Type Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::operator* 
          (
          const MatrixBase< OtherDerived > & 
          other)
           const [inline]
        

      







Computes the product of a Householder sequence with a matrix. 


Parameters:

  

    
[in]otherMatrix being multiplied. 

  

  




Returns:
Expression object representing the product.


This function computes 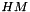$ HM $ where $ H $ is the Householder sequence represented by *this and $ M $ is the matrix other. 



Definition at line 357 of file HouseholderSequence.h.


    {
      typename internal::matrix_type_times_scalar_type<Scalar, OtherDerived>::Type
        res(other.template cast<typename internal::matrix_type_times_scalar_type<Scalar,OtherDerived>::ResultScalar>());
      applyThisOnTheLeft(res);
      return res;
    }













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          Index Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::rows 
          (
          void 
          )
           const [inline]
        

      







Number of rows of transformation viewed as a matrix. 


Returns:
Number of rows


This equals the dimension of the space that the transformation acts on. 



Reimplemented from Eigen::EigenBase< HouseholderSequence< VectorsType, CoeffsType, Side > >.



Definition at line 180 of file HouseholderSequence.h.


{ return Side==OnTheLeft ? m_vectors.rows() : m_vectors.cols(); }













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          HouseholderSequence& Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::setLength 
          (
          Index 
          length)
           [inline]
        

      







Sets the length of the Householder sequence. 


Parameters:

  

    
[in]lengthNew value for the length.

  

  




By default, the length 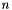$ n $ of the Householder sequence 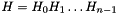$ H = H_0 H_1 \ldots H_{n-1} $ is set to the number of columns of the matrix v passed to the constructor, or the number of rows if that is smaller. After this function is called, the length equals length.


See also:
length() 



Definition at line 376 of file HouseholderSequence.h.


    {
      m_length = length;
      return *this;
    }













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          HouseholderSequence& Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::setShift 
          (
          Index 
          shift)
           [inline]
        

      







Sets the shift of the Householder sequence. 


Parameters:

  

    
[in]shiftNew value for the shift.

  

  




By default, a HouseholderSequence object represents 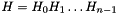$ H = H_0 H_1 \ldots H_{n-1} $ and the i-th column of the matrix v passed to the constructor corresponds to the i-th Householder reflection. After this function is called, the object represents 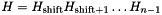$ H = H_{\mathrm{shift}} H_{\mathrm{shift}+1} \ldots H_{n-1} $ and the i-th column of v corresponds to the (shift+i)-th Householder reflection.


See also:
shift() 



Definition at line 393 of file HouseholderSequence.h.


    {
      m_shift = shift;
      return *this;
    }













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          HouseholderSequence& Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::setTrans 
          (
          bool 
          trans)
           [inline, protected]
        

      







Sets the transpose flag. 


Parameters:

  

    
[in]transNew value of the transpose flag.

  

  




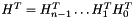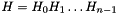By default, the transpose flag is not set. If the transpose flag is set, then this object represents $ H^T = H_{n-1}^T \ldots H_1^T H_0^T $ instead of $ H = H_0 H_1 \ldots H_{n-1} $.


See also:
trans() 



Definition at line 415 of file HouseholderSequence.h.


    {
      m_trans = trans;
      return *this;
    }













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          Index Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::shift 
          (
          )
           const [inline]
        

      







Returns the shift of the Householder sequence. 



Definition at line 400 of file HouseholderSequence.h.













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          bool Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::trans 
          (
          )
           const [inline, protected]
        

      







Returns the transpose flag. 



Definition at line 421 of file HouseholderSequence.h.













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          HouseholderSequence Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::transpose 
          (
          )
           const [inline]
        

      







Transpose of the Householder sequence. 



Definition at line 209 of file HouseholderSequence.h.


    {
      return HouseholderSequence(*this).setTrans(!m_trans);
    }







Friends And Related Function Documentation








template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          friend class HouseholderSequence [friend]
        

      







Definition at line 403 of file HouseholderSequence.h.













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          friend struct internal::hseq_side_dependent_impl [friend]
        

      







Definition at line 365 of file HouseholderSequence.h.







Member Data Documentation








template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          CoeffsType::Nested Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::m_coeffs [protected]
        

      







Definition at line 424 of file HouseholderSequence.h.













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          Index Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::m_length [protected]
        

      







Definition at line 426 of file HouseholderSequence.h.













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          Index Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::m_shift [protected]
        

      







Definition at line 427 of file HouseholderSequence.h.













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          bool Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::m_trans [protected]
        

      







Definition at line 425 of file HouseholderSequence.h.













template<typename VectorsType, typename CoeffsType, int Side> 

      

        

          VectorsType::Nested Eigen::HouseholderSequence< VectorsType, CoeffsType, Side >::m_vectors [protected]
        

      







Definition at line 423 of file HouseholderSequence.h.







The documentation for this class was generated from the following file:







 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Defines