Complete orthogonal decomposition (COD) of a matrix. More...

#include <CompleteOrthogonalDecomposition.h>

Collaboration diagram for Eigen::CompleteOrthogonalDecomposition< _MatrixType >:

Public Types
enum	{ RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, Options = MatrixType::Options, MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }
typedef _MatrixType	MatrixType
typedef MatrixType::Scalar	Scalar
typedef MatrixType::RealScalar	RealScalar
typedef MatrixType::StorageIndex	StorageIndex
typedef Matrix< Scalar, RowsAtCompileTime, RowsAtCompileTime, Options, MaxRowsAtCompileTime, MaxRowsAtCompileTime >	MatrixQType
typedef internal::plain_diag_type < MatrixType >::type	HCoeffsType
typedef PermutationMatrix < ColsAtCompileTime, MaxColsAtCompileTime >	PermutationType
typedef internal::plain_row_type < MatrixType, Index >::type	IntRowVectorType
typedef internal::plain_row_type < MatrixType >::type	RowVectorType
typedef internal::plain_row_type < MatrixType, RealScalar > ::type	RealRowVectorType
typedef HouseholderSequence < MatrixType, typename internal::remove_all< typename HCoeffsType::ConjugateReturnType > ::type >	HouseholderSequenceType
typedef MatrixType::PlainObject	PlainObject
Public Member Functions
	CompleteOrthogonalDecomposition ()
	Default Constructor.
	CompleteOrthogonalDecomposition (Index rows, Index cols)
	Default Constructor with memory preallocation.
template<typename InputType >
	CompleteOrthogonalDecomposition (const EigenBase< InputType > &matrix)
	Constructs a complete orthogonal decomposition from a given matrix.
template<typename Rhs >
const Solve < CompleteOrthogonalDecomposition, Rhs >	solve (const MatrixBase< Rhs > &b) const
HouseholderSequenceType	householderQ (void) const
HouseholderSequenceType	matrixQ (void) const
MatrixType	matrixZ () const
const MatrixType &	matrixQTZ () const
const MatrixType &	matrixT () const
template<typename InputType >
CompleteOrthogonalDecomposition &	compute (const EigenBase< InputType > &matrix)
const PermutationType &	colsPermutation () const
MatrixType::RealScalar	absDeterminant () const
MatrixType::RealScalar	logAbsDeterminant () const
Index	rank () const
Index	dimensionOfKernel () const
bool	isInjective () const
bool	isSurjective () const
bool	isInvertible () const
const Inverse < CompleteOrthogonalDecomposition >	pseudoInverse () const
Index	rows () const
Index	cols () const
const HCoeffsType &	hCoeffs () const
const HCoeffsType &	zCoeffs () const
CompleteOrthogonalDecomposition &	setThreshold (const RealScalar &threshold)
CompleteOrthogonalDecomposition &	setThreshold (Default_t)
RealScalar	threshold () const
Index	nonzeroPivots () const
RealScalar	maxPivot () const
ComputationInfo	info () const
	Reports whether the complete orthogonal decomposition was succesful.
template<typename RhsType , typename DstType >
EIGEN_DEVICE_FUNC void	_solve_impl (const RhsType &rhs, DstType &dst) const
Protected Member Functions
template<typename Rhs >
void	applyZAdjointOnTheLeftInPlace (Rhs &rhs) const
Static Protected Member Functions
static void	check_template_parameters ()
Protected Attributes
ColPivHouseholderQR< MatrixType >	m_cpqr
HCoeffsType	m_zCoeffs
RowVectorType	m_temp
Private Types
typedef PermutationType::Index	PermIndexType

Detailed Description

template<typename _MatrixType>
class Eigen::CompleteOrthogonalDecomposition< _MatrixType >

Complete orthogonal decomposition (COD) of a matrix.

Parameters:

MatrixType the type of the matrix of which we are computing the COD.

This class performs a rank-revealing complete ortogonal decomposition of a matrix A into matrices P, Q, T, and Z such that

$\mathbf{A} \, \mathbf{P} = \mathbf{Q} \, \begin{matrix} \mathbf{T} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \end{matrix} \, \mathbf{Z}$

by using Householder transformations. Here, P is a permutation matrix, Q and Z are unitary matrices and T an upper triangular matrix of size rank-by-rank. A may be rank deficient.

See also:: MatrixBase::completeOrthogonalDecomposition()

Definition at line 45 of file CompleteOrthogonalDecomposition.h.

Member Typedef Documentation

template<typename _MatrixType>

typedef internal::plain_diag_type<MatrixType>::type Eigen::CompleteOrthogonalDecomposition< _MatrixType >::HCoeffsType

Definition at line 61 of file CompleteOrthogonalDecomposition.h.

template<typename _MatrixType>

typedef HouseholderSequence< MatrixType, typename internal::remove_all< typename HCoeffsType::ConjugateReturnType>::type> Eigen::CompleteOrthogonalDecomposition< _MatrixType >::HouseholderSequenceType

Definition at line 72 of file CompleteOrthogonalDecomposition.h.

template<typename _MatrixType>

typedef internal::plain_row_type<MatrixType, Index>::type Eigen::CompleteOrthogonalDecomposition< _MatrixType >::IntRowVectorType

Definition at line 65 of file CompleteOrthogonalDecomposition.h.

template<typename _MatrixType>

typedef Matrix<Scalar, RowsAtCompileTime, RowsAtCompileTime, Options, MaxRowsAtCompileTime, MaxRowsAtCompileTime> Eigen::CompleteOrthogonalDecomposition< _MatrixType >::MatrixQType

Definition at line 60 of file CompleteOrthogonalDecomposition.h.

template<typename _MatrixType>

typedef _MatrixType Eigen::CompleteOrthogonalDecomposition< _MatrixType >::MatrixType

Definition at line 47 of file CompleteOrthogonalDecomposition.h.

template<typename _MatrixType>

typedef PermutationType::Index Eigen::CompleteOrthogonalDecomposition< _MatrixType >::PermIndexType [private]

Definition at line 76 of file CompleteOrthogonalDecomposition.h.

template<typename _MatrixType>

typedef PermutationMatrix<ColsAtCompileTime, MaxColsAtCompileTime> Eigen::CompleteOrthogonalDecomposition< _MatrixType >::PermutationType

Definition at line 63 of file CompleteOrthogonalDecomposition.h.

template<typename _MatrixType>

typedef MatrixType::PlainObject Eigen::CompleteOrthogonalDecomposition< _MatrixType >::PlainObject

Definition at line 73 of file CompleteOrthogonalDecomposition.h.

template<typename _MatrixType>

typedef internal::plain_row_type<MatrixType, RealScalar>::type Eigen::CompleteOrthogonalDecomposition< _MatrixType >::RealRowVectorType

Definition at line 68 of file CompleteOrthogonalDecomposition.h.

template<typename _MatrixType>

typedef MatrixType::RealScalar Eigen::CompleteOrthogonalDecomposition< _MatrixType >::RealScalar

Definition at line 56 of file CompleteOrthogonalDecomposition.h.

template<typename _MatrixType>

typedef internal::plain_row_type<MatrixType>::type Eigen::CompleteOrthogonalDecomposition< _MatrixType >::RowVectorType

Definition at line 66 of file CompleteOrthogonalDecomposition.h.

template<typename _MatrixType>

typedef MatrixType::Scalar Eigen::CompleteOrthogonalDecomposition< _MatrixType >::Scalar

Definition at line 55 of file CompleteOrthogonalDecomposition.h.

template<typename _MatrixType>

typedef MatrixType::StorageIndex Eigen::CompleteOrthogonalDecomposition< _MatrixType >::StorageIndex

Definition at line 57 of file CompleteOrthogonalDecomposition.h.

Member Enumeration Documentation

template<typename _MatrixType>

anonymous enum

Enumerator:

RowsAtCompileTime
ColsAtCompileTime
Options
MaxRowsAtCompileTime
MaxColsAtCompileTime

Definition at line 48 of file CompleteOrthogonalDecomposition.h.

       {
    RowsAtCompileTime = MatrixType::RowsAtCompileTime,
    ColsAtCompileTime = MatrixType::ColsAtCompileTime,
    Options = MatrixType::Options,
    MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime,
    MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime
  };

Constructor & Destructor Documentation

template<typename _MatrixType>

Eigen::CompleteOrthogonalDecomposition< _MatrixType >::CompleteOrthogonalDecomposition ( ) [inline]

Default Constructor.

The default constructor is useful in cases in which the user intends to perform decompositions via CompleteOrthogonalDecomposition::compute(const* MatrixType&).

Definition at line 86 of file CompleteOrthogonalDecomposition.h.

: m_cpqr(), m_zCoeffs(), m_temp() {}

template<typename _MatrixType>

Eigen::CompleteOrthogonalDecomposition< _MatrixType >::CompleteOrthogonalDecomposition	(	Index	rows,
		Index	cols
	)		`[inline]`

Default Constructor with memory preallocation.

Like the default constructor but with preallocation of the internal data according to the specified problem size.

See also:: CompleteOrthogonalDecomposition()

Definition at line 94 of file CompleteOrthogonalDecomposition.h.

      : m_cpqr(rows, cols), m_zCoeffs((std::min)(rows, cols)), m_temp(cols) {}

template<typename _MatrixType>

template<typename InputType >

Eigen::CompleteOrthogonalDecomposition< _MatrixType >::CompleteOrthogonalDecomposition ( const EigenBase< InputType > & matrix ) [inline, explicit]

Constructs a complete orthogonal decomposition from a given matrix.

This constructor computes the complete orthogonal decomposition of the matrix matrix by calling the method compute(). The default threshold for rank determination will be used. It is a short cut for:

 CompleteOrthogonalDecomposition<MatrixType> cod(matrix.rows(),
                                                 matrix.cols());
 cod.setThreshold(Default);
 cod.compute(matrix);

See also:: compute()

Definition at line 114 of file CompleteOrthogonalDecomposition.h.

      : m_cpqr(matrix.rows(), matrix.cols()),
        m_zCoeffs((std::min)(matrix.rows(), matrix.cols())),
        m_temp(matrix.cols()) {
    compute(matrix.derived());
  }

Member Function Documentation

template<typename _MatrixType >

template<typename RhsType , typename DstType >

void Eigen::CompleteOrthogonalDecomposition< _MatrixType >::_solve_impl	(	const RhsType &	rhs,
		DstType &	dst
	)		const

Definition at line 470 of file CompleteOrthogonalDecomposition.h.

                                            {
  eigen_assert(rhs.rows() == this->rows());

  const Index rank = this->rank();
  if (rank == 0) {
    dst.setZero();
    return;
  }

  // Compute c = Q^* * rhs
  // Note that the matrix Q = H_0^* H_1^*... so its inverse is
  // Q^* = (H_0 H_1 ...)^T
  typename RhsType::PlainObject c(rhs);
  c.applyOnTheLeft(
      householderSequence(matrixQTZ(), hCoeffs()).setLength(rank).transpose());

  // Solve T z = c(1:rank, :)
  dst.topRows(rank) = matrixT()
                          .topLeftCorner(rank, rank)
                          .template triangularView<Upper>()
                          .solve(c.topRows(rank));

  const Index cols = this->cols();
  if (rank < cols) {
    // Compute y = Z^* * [ z ]
    //                   [ 0 ]
    dst.bottomRows(cols - rank).setZero();
    applyZAdjointOnTheLeftInPlace(dst);
  }

  // Undo permutation to get x = P^{-1} * y.
  dst = colsPermutation() * dst;
}

template<typename MatrixType >

MatrixType::RealScalar Eigen::CompleteOrthogonalDecomposition< MatrixType >::absDeterminant ( ) const

Returns:: the absolute value of the determinant of the matrix of which *this is the complete orthogonal decomposition. It has only linear complexity (that is, O(n) where n is the dimension of the square matrix) as the complete orthogonal decomposition has already been computed.

Note:: This is only for square matrices.

Warning:: a determinant can be very big or small, so for matrices of large enough dimension, there is a risk of overflow/underflow. One way to work around that is to use logAbsDeterminant() instead.

See also:: logAbsDeterminant(), MatrixBase::determinant()

Definition at line 369 of file CompleteOrthogonalDecomposition.h.

                                                                  {
  return m_cpqr.absDeterminant();
}

template<typename MatrixType >

template<typename Rhs >

void Eigen::CompleteOrthogonalDecomposition< MatrixType >::applyZAdjointOnTheLeftInPlace ( Rhs & rhs ) const [protected]

Overwrites rhs with $\mathbf{Z}^* * \mathbf{rhs}$ .

Definition at line 447 of file CompleteOrthogonalDecomposition.h.

                    {
  const Index cols = this->cols();
  const Index nrhs = rhs.cols();
  const Index rank = this->rank();
  Matrix<typename MatrixType::Scalar, Dynamic, 1> temp((std::max)(cols, nrhs));
  for (Index k = 0; k < rank; ++k) {
    if (k != rank - 1) {
      rhs.row(k).swap(rhs.row(rank - 1));
    }
    rhs.middleRows(rank - 1, cols - rank + 1)
        .applyHouseholderOnTheLeft(
            matrixQTZ().row(k).tail(cols - rank).adjoint(), zCoeffs()(k),
            &temp(0));
    if (k != rank - 1) {
      rhs.row(k).swap(rhs.row(rank - 1));
    }
  }
}

template<typename _MatrixType>

static void Eigen::CompleteOrthogonalDecomposition< _MatrixType >::check_template_parameters ( ) [inline, static, protected]

Definition at line 353 of file CompleteOrthogonalDecomposition.h.

                                          {
    EIGEN_STATIC_ASSERT_NON_INTEGER(Scalar);
  }

template<typename _MatrixType>

Index Eigen::CompleteOrthogonalDecomposition< _MatrixType >::cols ( void ) const [inline]

Definition at line 261 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.cols(); }

template<typename _MatrixType>

const PermutationType& Eigen::CompleteOrthogonalDecomposition< _MatrixType >::colsPermutation ( ) const [inline]

Returns:: a const reference to the column permutation matrix

Definition at line 171 of file CompleteOrthogonalDecomposition.h.

                                                 {
    return m_cpqr.colsPermutation();
  }

template<typename MatrixType >

template<typename InputType >

CompleteOrthogonalDecomposition< MatrixType > & Eigen::CompleteOrthogonalDecomposition< MatrixType >::compute ( const EigenBase< InputType > & matrix )

Performs the complete orthogonal decomposition of the given matrix matrix. The result of the factorization is stored into *this, and a reference to *this is returned.

See also:: class CompleteOrthogonalDecomposition, CompleteOrthogonalDecomposition(const MatrixType&)

Definition at line 389 of file CompleteOrthogonalDecomposition.h.

                                                           {
  check_template_parameters();

  // the column permutation is stored as int indices, so just to be sure:
  eigen_assert(matrix.cols() <= NumTraits<int>::highest());

  // Compute the column pivoted QR factorization A P = Q R.
  m_cpqr.compute(matrix);

  const Index rank = m_cpqr.rank();
  const Index cols = matrix.cols();
  if (rank < cols) {
    // We have reduced the (permuted) matrix to the form
    //   [R11 R12]
    //   [ 0  R22]
    // where R11 is r-by-r (r = rank) upper triangular, R12 is
    // r-by-(n-r), and R22 is empty or the norm of R22 is negligible.
    // We now compute the complete orthogonal decomposition by applying
    // Householder transformations from the right to the upper trapezoidal
    // matrix X = [R11 R12] to zero out R12 and obtain the factorization
    // [R11 R12] = [T11 0] * Z, where T11 is r-by-r upper triangular and
    // Z = Z(0) * Z(1) ... Z(r-1) is an n-by-n orthogonal matrix.
    // We store the data representing Z in R12 and m_zCoeffs.
    for (Index k = rank - 1; k >= 0; --k) {
      if (k != rank - 1) {
        // Given the API for Householder reflectors, it is more convenient if
        // we swap the leading parts of columns k and r-1 (zero-based) to form
        // the matrix X_k = [X(0:k, k), X(0:k, r:n)]
        m_cpqr.m_qr.col(k).head(k + 1).swap(
            m_cpqr.m_qr.col(rank - 1).head(k + 1));
      }
      // Construct Householder reflector Z(k) to zero out the last row of X_k,
      // i.e. choose Z(k) such that
      // [X(k, k), X(k, r:n)] * Z(k) = [beta, 0, .., 0].
      RealScalar beta;
      m_cpqr.m_qr.row(k)
          .tail(cols - rank + 1)
          .makeHouseholderInPlace(m_zCoeffs(k), beta);
      m_cpqr.m_qr(k, rank - 1) = beta;
      if (k > 0) {
        // Apply Z(k) to the first k rows of X_k
        m_cpqr.m_qr.topRightCorner(k, cols - rank + 1)
            .applyHouseholderOnTheRight(
                m_cpqr.m_qr.row(k).tail(cols - rank).transpose(), m_zCoeffs(k),
                &m_temp(0));
      }
      if (k != rank - 1) {
        // Swap X(0:k,k) back to its proper location.
        m_cpqr.m_qr.col(k).head(k + 1).swap(
            m_cpqr.m_qr.col(rank - 1).head(k + 1));
      }
    }
  }
  return *this;
}

template<typename _MatrixType>

Index Eigen::CompleteOrthogonalDecomposition< _MatrixType >::dimensionOfKernel ( ) const [inline]

Returns:: the dimension of the kernel of the matrix of which *this is the complete orthogonal decomposition.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 221 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.dimensionOfKernel(); }

template<typename _MatrixType>

const HCoeffsType& Eigen::CompleteOrthogonalDecomposition< _MatrixType >::hCoeffs ( ) const [inline]

Returns:: a const reference to the vector of Householder coefficients used to represent the factor Q.

For advanced uses only.

Definition at line 268 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.hCoeffs(); }

template<typename MatrixType >

CompleteOrthogonalDecomposition< MatrixType >::HouseholderSequenceType Eigen::CompleteOrthogonalDecomposition< MatrixType >::householderQ ( void ) const

Returns:: the matrix Q as a sequence of householder transformations

Definition at line 524 of file CompleteOrthogonalDecomposition.h.

                                                                {
  return m_cpqr.householderQ();
}

template<typename _MatrixType>

ComputationInfo Eigen::CompleteOrthogonalDecomposition< _MatrixType >::info ( ) const [inline]

Reports whether the complete orthogonal decomposition was succesful.

Note:: This function always returns Success. It is provided for compatibility with other factorization routines.

Returns:: Success

Definition at line 342 of file CompleteOrthogonalDecomposition.h.

                               {
    eigen_assert(m_cpqr.m_isInitialized && "Decomposition is not initialized.");
    return Success;
  }

template<typename _MatrixType>

bool Eigen::CompleteOrthogonalDecomposition< _MatrixType >::isInjective ( ) const [inline]

Returns:: true if the matrix of which *this is the decomposition represents an injective linear map, i.e. has trivial kernel; false otherwise.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 230 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.isInjective(); }

template<typename _MatrixType>

bool Eigen::CompleteOrthogonalDecomposition< _MatrixType >::isInvertible ( ) const [inline]

Returns:: true if the matrix of which *this is the complete orthogonal decomposition is invertible.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 248 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.isInvertible(); }

template<typename _MatrixType>

bool Eigen::CompleteOrthogonalDecomposition< _MatrixType >::isSurjective ( ) const [inline]

Returns:: true if the matrix of which *this is the decomposition represents a surjective linear map; false otherwise.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 239 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.isSurjective(); }

template<typename MatrixType >

MatrixType::RealScalar Eigen::CompleteOrthogonalDecomposition< MatrixType >::logAbsDeterminant ( ) const

Returns:: the natural log of the absolute value of the determinant of the matrix of which *this is the complete orthogonal decomposition. It has only linear complexity (that is, O(n) where n is the dimension of the square matrix) as the complete orthogonal decomposition has already been computed.

Note:: This is only for square matrices.; This method is useful to work around the risk of overflow/underflow that's inherent to determinant computation.

See also:: absDeterminant(), MatrixBase::determinant()

Definition at line 375 of file CompleteOrthogonalDecomposition.h.

                                                                     {
  return m_cpqr.logAbsDeterminant();
}

template<typename _MatrixType>

HouseholderSequenceType Eigen::CompleteOrthogonalDecomposition< _MatrixType >::matrixQ ( void ) const [inline]

Definition at line 139 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.householderQ(); }

template<typename _MatrixType>

const MatrixType& Eigen::CompleteOrthogonalDecomposition< _MatrixType >::matrixQTZ ( ) const [inline]

Returns:: a reference to the matrix where the complete orthogonal decomposition is stored

Definition at line 152 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.matrixQR(); }

template<typename _MatrixType>

const MatrixType& Eigen::CompleteOrthogonalDecomposition< _MatrixType >::matrixT ( ) const [inline]

Returns:: a reference to the matrix where the complete orthogonal decomposition is stored.

Warning:

The strict lower part and

 cols() - rank()

right columns of this matrix contains internal values. Only the upper triangular part should be referenced. To get it, use

 matrixT().template triangularView<Upper>()

For rank-deficient matrices, use

 matrixR().topLeftCorner(rank(), rank()).template triangularView<Upper>()

Definition at line 165 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.matrixQR(); }

template<typename _MatrixType>

MatrixType Eigen::CompleteOrthogonalDecomposition< _MatrixType >::matrixZ ( ) const [inline]

Returns:: the matrix Z.

Definition at line 143 of file CompleteOrthogonalDecomposition.h.

                             {
    MatrixType Z = MatrixType::Identity(m_cpqr.cols(), m_cpqr.cols());
    applyZAdjointOnTheLeftInPlace(Z);
    return Z.adjoint();
  }

template<typename _MatrixType>

RealScalar Eigen::CompleteOrthogonalDecomposition< _MatrixType >::maxPivot ( ) const [inline]

Returns:: the absolute value of the biggest pivot, i.e. the biggest diagonal coefficient of R.

Definition at line 332 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.maxPivot(); }

template<typename _MatrixType>

Index Eigen::CompleteOrthogonalDecomposition< _MatrixType >::nonzeroPivots ( ) const [inline]

Returns:: the number of nonzero pivots in the complete orthogonal decomposition. Here nonzero is meant in the exact sense, not in a fuzzy sense. So that notion isn't really intrinsically interesting, but it is still useful when implementing algorithms.

See also:: rank()

Definition at line 327 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.nonzeroPivots(); }

template<typename _MatrixType>

const Inverse<CompleteOrthogonalDecomposition> Eigen::CompleteOrthogonalDecomposition< _MatrixType >::pseudoInverse ( ) const [inline]

Returns:: the pseudo-inverse of the matrix of which *this is the complete orthogonal decomposition.

Warning:: : Do not compute this->pseudoInverse()*rhs to solve a linear systems. It is more efficient and numerically stable to call this->solve(rhs).

Definition at line 255 of file CompleteOrthogonalDecomposition.h.

  {
    return Inverse<CompleteOrthogonalDecomposition>(*this);
  }

template<typename _MatrixType>

Index Eigen::CompleteOrthogonalDecomposition< _MatrixType >::rank ( ) const [inline]

Returns:: the rank of the matrix of which *this is the complete orthogonal decomposition.

Note:: This method has to determine which pivots should be considered nonzero. For that, it uses the threshold value that you can control by calling setThreshold(const RealScalar&).

Definition at line 212 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.rank(); }

template<typename _MatrixType>

Index Eigen::CompleteOrthogonalDecomposition< _MatrixType >::rows ( void ) const [inline]

Definition at line 260 of file CompleteOrthogonalDecomposition.h.

{ return m_cpqr.rows(); }

template<typename _MatrixType>

CompleteOrthogonalDecomposition& Eigen::CompleteOrthogonalDecomposition< _MatrixType >::setThreshold ( const RealScalar & threshold ) [inline]

Allows to prescribe a threshold to be used by certain methods, such as rank(), who need to determine when pivots are to be considered nonzero. Most be called before calling compute().

When it needs to get the threshold value, Eigen calls threshold(). By default, this uses a formula to automatically determine a reasonable threshold. Once you have called the present method setThreshold(const RealScalar&), your value is used instead.

Parameters:

threshold The new value to use as the threshold.

A pivot will be considered nonzero if its absolute value is strictly greater than 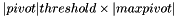$\vert pivot \vert \leqslant threshold \times \vert maxpivot \vert$ where maxpivot is the biggest pivot.

If you want to come back to the default behavior, call setThreshold(Default_t)

Definition at line 296 of file CompleteOrthogonalDecomposition.h.

                                                                             {
    m_cpqr.setThreshold(threshold);
    return *this;
  }

template<typename _MatrixType>

CompleteOrthogonalDecomposition& Eigen::CompleteOrthogonalDecomposition< _MatrixType >::setThreshold ( Default_t ) [inline]

Allows to come back to the default behavior, letting Eigen use its default formula for determining the threshold.

You should pass the special object Eigen::Default as parameter here.

 qr.setThreshold(Eigen::Default);

See the documentation of setThreshold(const RealScalar&).

Definition at line 309 of file CompleteOrthogonalDecomposition.h.

                                                           {
    m_cpqr.setThreshold(Default);
    return *this;
  }

template<typename _MatrixType>

template<typename Rhs >

const Solve<CompleteOrthogonalDecomposition, Rhs> Eigen::CompleteOrthogonalDecomposition< _MatrixType >::solve ( const MatrixBase< Rhs > & b ) const [inline]

This method computes the minimum-norm solution X to a least squares problem

$\mathrm{minimize} ||A X - B||$

, where A is the matrix of which *this is the complete orthogonal decomposition.

Parameters:

B	the right-hand sides of the problem to solve.

Returns:: a solution.

Definition at line 131 of file CompleteOrthogonalDecomposition.h.

                                      {
    eigen_assert(m_cpqr.m_isInitialized &&
                 "CompleteOrthogonalDecomposition is not initialized.");
    return Solve<CompleteOrthogonalDecomposition, Rhs>(*this, b.derived());
  }

template<typename _MatrixType>

RealScalar Eigen::CompleteOrthogonalDecomposition< _MatrixType >::threshold ( ) const [inline]

Returns the threshold that will be used by certain methods such as rank().

See the documentation of setThreshold(const RealScalar&).

Definition at line 318 of file CompleteOrthogonalDecomposition.h.