MOAB  4.9.3pre
Public Types | Public Member Functions | Protected Types | Protected Attributes | Friends
Eigen::SparseQR< _MatrixType, _OrderingType > Class Template Reference

Sparse left-looking rank-revealing QR factorization. More...

#include <SparseQR.h>

Inheritance diagram for Eigen::SparseQR< _MatrixType, _OrderingType >:
Inheritance graph
[legend]
Collaboration diagram for Eigen::SparseQR< _MatrixType, _OrderingType >:
Collaboration graph
[legend]

List of all members.

Public Types

enum  { ColsAtCompileTime = MatrixType::ColsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }
typedef _MatrixType MatrixType
typedef _OrderingType OrderingType
typedef MatrixType::Scalar Scalar
typedef MatrixType::RealScalar RealScalar
typedef MatrixType::StorageIndex StorageIndex
typedef SparseMatrix< Scalar,
ColMajor, StorageIndex > 		QRMatrixType
typedef Matrix< StorageIndex,
Dynamic, 1 > 		IndexVector
typedef Matrix< Scalar,
Dynamic, 1 > 		ScalarVector
typedef PermutationMatrix
< Dynamic, Dynamic,
StorageIndex > 		PermutationType

Public Member Functions

 SparseQR ()
 SparseQR (const MatrixType &mat)
void compute (const MatrixType &mat)
void analyzePattern (const MatrixType &mat)
 Preprocessing step of a QR factorization.
void factorize (const MatrixType &mat)
 Performs the numerical QR factorization of the input matrix.
Index rows () const
Index cols () const
const QRMatrixType & matrixR () const
Index rank () const
SparseQRMatrixQReturnType
< SparseQR > 		matrixQ () const
const PermutationType & colsPermutation () const
std::string lastErrorMessage () const
template<typename Rhs , typename Dest >
bool _solve_impl (const MatrixBase< Rhs > &B, MatrixBase< Dest > &dest) const
void setPivotThreshold (const RealScalar &threshold)
template<typename Rhs >
const Solve< SparseQR, Rhs > solve (const MatrixBase< Rhs > &B) const
template<typename Rhs >
const Solve< SparseQR, Rhs > solve (const SparseMatrixBase< Rhs > &B) const
ComputationInfo info () const
 Reports whether previous computation was successful.
void _sort_matrix_Q ()

Protected Types

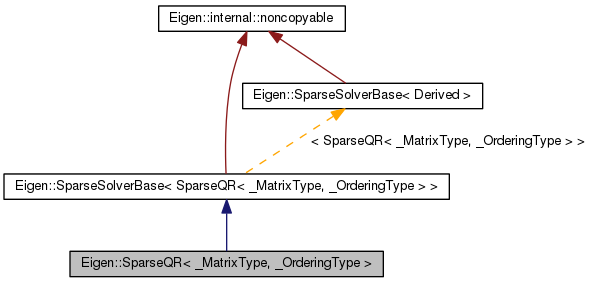
typedef SparseSolverBase
< SparseQR< _MatrixType,
_OrderingType > > 		Base

Protected Attributes

bool m_analysisIsok
bool m_factorizationIsok
ComputationInfo m_info
std::string m_lastError
QRMatrixType m_pmat
QRMatrixType m_R
QRMatrixType m_Q
ScalarVector m_hcoeffs
PermutationType m_perm_c
PermutationType m_pivotperm
PermutationType m_outputPerm_c
RealScalar m_threshold
bool m_useDefaultThreshold
Index m_nonzeropivots
IndexVector m_etree
IndexVector m_firstRowElt
bool m_isQSorted
bool m_isEtreeOk

Friends

struct SparseQR_QProduct

Detailed Description

template<typename _MatrixType, typename _OrderingType>
class Eigen::SparseQR< _MatrixType, _OrderingType >

Sparse left-looking rank-revealing QR factorization.

This class implements a left-looking rank-revealing QR decomposition of sparse matrices. When a column has a norm less than a given tolerance it is implicitly permuted to the end. The QR factorization thus obtained is given by A*P = Q*R where R is upper triangular or trapezoidal.

P is the column permutation which is the product of the fill-reducing and the rank-revealing permutations. Use colsPermutation() to get it.

Q is the orthogonal matrix represented as products of Householder reflectors. Use matrixQ() to get an expression and matrixQ().transpose() to get the transpose. You can then apply it to a vector.

R is the sparse triangular or trapezoidal matrix. The later occurs when A is rank-deficient. matrixR().topLeftCorner(rank(), rank()) always returns a triangular factor of full rank.

Template Parameters:
_MatrixTypeThe type of the sparse matrix A, must be a column-major SparseMatrix<>
_OrderingTypeThe fill-reducing ordering method. See the OrderingMethods module for the list of built-in and external ordering methods.
Warning:
The input sparse matrix A must be in compressed mode (see SparseMatrix::makeCompressed()).

Definition at line 71 of file SparseQR.h.

Member Typedef Documentation

template<typename _MatrixType , typename _OrderingType >
typedef SparseSolverBase<SparseQR<_MatrixType,_OrderingType> > Eigen::SparseQR< _MatrixType, _OrderingType >::Base [protected]

Definition at line 74 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
typedef Matrix<StorageIndex, Dynamic, 1> Eigen::SparseQR< _MatrixType, _OrderingType >::IndexVector

Definition at line 84 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
typedef _MatrixType Eigen::SparseQR< _MatrixType, _OrderingType >::MatrixType

Definition at line 78 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
typedef _OrderingType Eigen::SparseQR< _MatrixType, _OrderingType >::OrderingType

Definition at line 79 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
typedef PermutationMatrix<Dynamic, Dynamic, StorageIndex> Eigen::SparseQR< _MatrixType, _OrderingType >::PermutationType

Definition at line 86 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
typedef SparseMatrix<Scalar,ColMajor,StorageIndex> Eigen::SparseQR< _MatrixType, _OrderingType >::QRMatrixType

Definition at line 83 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
typedef MatrixType::RealScalar Eigen::SparseQR< _MatrixType, _OrderingType >::RealScalar

Definition at line 81 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
typedef MatrixType::Scalar Eigen::SparseQR< _MatrixType, _OrderingType >::Scalar

Definition at line 80 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
typedef Matrix<Scalar, Dynamic, 1> Eigen::SparseQR< _MatrixType, _OrderingType >::ScalarVector

Definition at line 85 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
typedef MatrixType::StorageIndex Eigen::SparseQR< _MatrixType, _OrderingType >::StorageIndex

Definition at line 82 of file SparseQR.h.

Member Enumeration Documentation

template<typename _MatrixType , typename _OrderingType >
anonymous enum
Enumerator:
ColsAtCompileTime 
MaxColsAtCompileTime 

Definition at line 88 of file SparseQR.h.

         {
      ColsAtCompileTime = MatrixType::ColsAtCompileTime,
      MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime
    };

Constructor & Destructor Documentation

template<typename _MatrixType , typename _OrderingType >
Eigen::SparseQR< _MatrixType, _OrderingType >::SparseQR ( ) [inline]

Definition at line 94 of file SparseQR.h.

                :  m_analysisIsok(false), m_lastError(""), m_useDefaultThreshold(true),m_isQSorted(false),m_isEtreeOk(false)
    { }
template<typename _MatrixType , typename _OrderingType >
Eigen::SparseQR< _MatrixType, _OrderingType >::SparseQR ( const MatrixType &  mat) [inline, explicit]

Construct a QR factorization of the matrix mat.

Warning:
The matrix mat must be in compressed mode (see SparseMatrix::makeCompressed()).
See also:
compute()

Definition at line 103 of file SparseQR.h.

                                             : m_analysisIsok(false), m_lastError(""), m_useDefaultThreshold(true),m_isQSorted(false),m_isEtreeOk(false)
    {
      compute(mat);
    }

Member Function Documentation

template<typename _MatrixType , typename _OrderingType >
template<typename Rhs , typename Dest >
bool Eigen::SparseQR< _MatrixType, _OrderingType >::_solve_impl ( const MatrixBase< Rhs > &  B,
MatrixBase< Dest > &  dest 
) const [inline]

Definition at line 192 of file SparseQR.h.

    {
      eigen_assert(m_isInitialized && "The factorization should be called first, use compute()");
      eigen_assert(this->rows() == B.rows() && "SparseQR::solve() : invalid number of rows in the right hand side matrix");

      Index rank = this->rank();
      
      // Compute Q^T * b;
      typename Dest::PlainObject y, b;
      y = this->matrixQ().transpose() * B; 
      b = y;
      
      // Solve with the triangular matrix R
      y.resize((std::max<Index>)(cols(),y.rows()),y.cols());
      y.topRows(rank) = this->matrixR().topLeftCorner(rank, rank).template triangularView<Upper>().solve(b.topRows(rank));
      y.bottomRows(y.rows()-rank).setZero();
      
      // Apply the column permutation
      if (m_perm_c.size())  dest = colsPermutation() * y.topRows(cols());
      else                  dest = y.topRows(cols());
      
      m_info = Success;
      return true;
    }
template<typename _MatrixType , typename _OrderingType >
void Eigen::SparseQR< _MatrixType, _OrderingType >::_sort_matrix_Q ( ) [inline]

Definition at line 263 of file SparseQR.h.

    {
      if(this->m_isQSorted) return;
      // The matrix Q is sorted during the transposition
      SparseMatrix<Scalar, RowMajor, Index> mQrm(this->m_Q);
      this->m_Q = mQrm;
      this->m_isQSorted = true;
    }
template<typename MatrixType , typename OrderingType >
void Eigen::SparseQR< MatrixType, OrderingType >::analyzePattern ( const MatrixType &  mat)

Preprocessing step of a QR factorization.

Warning:
The matrix mat must be in compressed mode (see SparseMatrix::makeCompressed()).

In this step, the fill-reducing permutation is computed and applied to the columns of A and the column elimination tree is computed as well. Only the sparsity pattern of mat is exploited.

Note:
In this step it is assumed that there is no empty row in the matrix mat.

Definition at line 307 of file SparseQR.h.

{
  eigen_assert(mat.isCompressed() && "SparseQR requires a sparse matrix in compressed mode. Call .makeCompressed() before passing it to SparseQR");
  // Copy to a column major matrix if the input is rowmajor
  typename internal::conditional<MatrixType::IsRowMajor,QRMatrixType,const MatrixType&>::type matCpy(mat);
  // Compute the column fill reducing ordering
  OrderingType ord; 
  ord(matCpy, m_perm_c); 
  Index n = mat.cols();
  Index m = mat.rows();
  Index diagSize = (std::min)(m,n);
  
  if (!m_perm_c.size())
  {
    m_perm_c.resize(n);
    m_perm_c.indices().setLinSpaced(n, 0,StorageIndex(n-1));
  }
  
  // Compute the column elimination tree of the permuted matrix
  m_outputPerm_c = m_perm_c.inverse();
  internal::coletree(matCpy, m_etree, m_firstRowElt, m_outputPerm_c.indices().data());
  m_isEtreeOk = true;
  
  m_R.resize(m, n);
  m_Q.resize(m, diagSize);
  
  // Allocate space for nonzero elements : rough estimation
  m_R.reserve(2*mat.nonZeros()); //FIXME Get a more accurate estimation through symbolic factorization with the etree
  m_Q.reserve(2*mat.nonZeros());
  m_hcoeffs.resize(diagSize);
  m_analysisIsok = true;
}
template<typename _MatrixType , typename _OrderingType >
Index Eigen::SparseQR< _MatrixType, _OrderingType >::cols ( void  ) const [inline]
Returns:
the number of columns of the represented matrix.

Definition at line 128 of file SparseQR.h.

{ return m_pmat.cols();}
template<typename _MatrixType , typename _OrderingType >
const PermutationType& Eigen::SparseQR< _MatrixType, _OrderingType >::colsPermutation ( ) const [inline]
Returns:
a const reference to the column permutation P that was applied to A such that A*P = Q*R It is the combination of the fill-in reducing permutation and numerical column pivoting.

Definition at line 179 of file SparseQR.h.

    { 
      eigen_assert(m_isInitialized && "Decomposition is not initialized.");
      return m_outputPerm_c;
    }
template<typename _MatrixType , typename _OrderingType >
void Eigen::SparseQR< _MatrixType, _OrderingType >::compute ( const MatrixType &  mat) [inline]

Computes the QR factorization of the sparse matrix mat.

Warning:
The matrix mat must be in compressed mode (see SparseMatrix::makeCompressed()).
See also:
analyzePattern(), factorize()

Definition at line 114 of file SparseQR.h.

    {
      analyzePattern(mat);
      factorize(mat);
    }
template<typename MatrixType , typename OrderingType >
void Eigen::SparseQR< MatrixType, OrderingType >::factorize ( const MatrixType &  mat)

Performs the numerical QR factorization of the input matrix.

The function SparseQR::analyzePattern(const MatrixType&) must have been called beforehand with a matrix having the same sparsity pattern than mat.

Parameters:
matThe sparse column-major matrix

Definition at line 348 of file SparseQR.h.

{
  using std::abs;
  
  eigen_assert(m_analysisIsok && "analyzePattern() should be called before this step");
  StorageIndex m = StorageIndex(mat.rows());
  StorageIndex n = StorageIndex(mat.cols());
  StorageIndex diagSize = (std::min)(m,n);
  IndexVector mark((std::max)(m,n)); mark.setConstant(-1);  // Record the visited nodes
  IndexVector Ridx(n), Qidx(m);                             // Store temporarily the row indexes for the current column of R and Q
  Index nzcolR, nzcolQ;                                     // Number of nonzero for the current column of R and Q
  ScalarVector tval(m);                                     // The dense vector used to compute the current column
  RealScalar pivotThreshold = m_threshold;
  
  m_R.setZero();
  m_Q.setZero();
  m_pmat = mat;
  if(!m_isEtreeOk)
  {
    m_outputPerm_c = m_perm_c.inverse();
    internal::coletree(m_pmat, m_etree, m_firstRowElt, m_outputPerm_c.indices().data());
    m_isEtreeOk = true;
  }

  m_pmat.uncompress(); // To have the innerNonZeroPtr allocated
  
  // Apply the fill-in reducing permutation lazily:
  {
    // If the input is row major, copy the original column indices,
    // otherwise directly use the input matrix
    // 
    IndexVector originalOuterIndicesCpy;
    const StorageIndex *originalOuterIndices = mat.outerIndexPtr();
    if(MatrixType::IsRowMajor)
    {
      originalOuterIndicesCpy = IndexVector::Map(m_pmat.outerIndexPtr(),n+1);
      originalOuterIndices = originalOuterIndicesCpy.data();
    }
    
    for (int i = 0; i < n; i++)
    {
      Index p = m_perm_c.size() ? m_perm_c.indices()(i) : i;
      m_pmat.outerIndexPtr()[p] = originalOuterIndices[i]; 
      m_pmat.innerNonZeroPtr()[p] = originalOuterIndices[i+1] - originalOuterIndices[i]; 
    }
  }
  
  /* Compute the default threshold as in MatLab, see:
   * Tim Davis, "Algorithm 915, SuiteSparseQR: Multifrontal Multithreaded Rank-Revealing
   * Sparse QR Factorization, ACM Trans. on Math. Soft. 38(1), 2011, Page 8:3 
   */
  if(m_useDefaultThreshold) 
  {
    RealScalar max2Norm = 0.0;
    for (int j = 0; j < n; j++) max2Norm = numext::maxi(max2Norm, m_pmat.col(j).norm());
    if(max2Norm==RealScalar(0))
      max2Norm = RealScalar(1);
    pivotThreshold = 20 * (m + n) * max2Norm * NumTraits<RealScalar>::epsilon();
  }
  
  // Initialize the numerical permutation
  m_pivotperm.setIdentity(n);
  
  StorageIndex nonzeroCol = 0; // Record the number of valid pivots
  m_Q.startVec(0);

  // Left looking rank-revealing QR factorization: compute a column of R and Q at a time
  for (StorageIndex col = 0; col < n; ++col)
  {
    mark.setConstant(-1);
    m_R.startVec(col);
    mark(nonzeroCol) = col;
    Qidx(0) = nonzeroCol;
    nzcolR = 0; nzcolQ = 1;
    bool found_diag = nonzeroCol>=m;
    tval.setZero(); 
    
    // Symbolic factorization: find the nonzero locations of the column k of the factors R and Q, i.e.,
    // all the nodes (with indexes lower than rank) reachable through the column elimination tree (etree) rooted at node k.
    // Note: if the diagonal entry does not exist, then its contribution must be explicitly added,
    // thus the trick with found_diag that permits to do one more iteration on the diagonal element if this one has not been found.
    for (typename QRMatrixType::InnerIterator itp(m_pmat, col); itp || !found_diag; ++itp)
    {
      StorageIndex curIdx = nonzeroCol;
      if(itp) curIdx = StorageIndex(itp.row());
      if(curIdx == nonzeroCol) found_diag = true;
      
      // Get the nonzeros indexes of the current column of R
      StorageIndex st = m_firstRowElt(curIdx); // The traversal of the etree starts here
      if (st < 0 )
      {
        m_lastError = "Empty row found during numerical factorization";
        m_info = InvalidInput;
        return;
      }

      // Traverse the etree 
      Index bi = nzcolR;
      for (; mark(st) != col; st = m_etree(st))
      {
        Ridx(nzcolR) = st;  // Add this row to the list,
        mark(st) = col;     // and mark this row as visited
        nzcolR++;
      }

      // Reverse the list to get the topological ordering
      Index nt = nzcolR-bi;
      for(Index i = 0; i < nt/2; i++) std::swap(Ridx(bi+i), Ridx(nzcolR-i-1));
       
      // Copy the current (curIdx,pcol) value of the input matrix
      if(itp) tval(curIdx) = itp.value();
      else    tval(curIdx) = Scalar(0);
      
      // Compute the pattern of Q(:,k)
      if(curIdx > nonzeroCol && mark(curIdx) != col ) 
      {
        Qidx(nzcolQ) = curIdx;  // Add this row to the pattern of Q,
        mark(curIdx) = col;     // and mark it as visited
        nzcolQ++;
      }
    }

    // Browse all the indexes of R(:,col) in reverse order
    for (Index i = nzcolR-1; i >= 0; i--)
    {
      Index curIdx = Ridx(i);
      
      // Apply the curIdx-th householder vector to the current column (temporarily stored into tval)
      Scalar tdot(0);
      
      // First compute q' * tval
      tdot = m_Q.col(curIdx).dot(tval);

      tdot *= m_hcoeffs(curIdx);
      
      // Then update tval = tval - q * tau
      // FIXME: tval -= tdot * m_Q.col(curIdx) should amount to the same (need to check/add support for efficient "dense ?= sparse")
      for (typename QRMatrixType::InnerIterator itq(m_Q, curIdx); itq; ++itq)
        tval(itq.row()) -= itq.value() * tdot;

      // Detect fill-in for the current column of Q
      if(m_etree(Ridx(i)) == nonzeroCol)
      {
        for (typename QRMatrixType::InnerIterator itq(m_Q, curIdx); itq; ++itq)
        {
          StorageIndex iQ = StorageIndex(itq.row());
          if (mark(iQ) != col)
          {
            Qidx(nzcolQ++) = iQ;  // Add this row to the pattern of Q,
            mark(iQ) = col;       // and mark it as visited
          }
        }
      }
    } // End update current column
    
    Scalar tau = RealScalar(0);
    RealScalar beta = 0;
    
    if(nonzeroCol < diagSize)
    {
      // Compute the Householder reflection that eliminate the current column
      // FIXME this step should call the Householder module.
      Scalar c0 = nzcolQ ? tval(Qidx(0)) : Scalar(0);
      
      // First, the squared norm of Q((col+1):m, col)
      RealScalar sqrNorm = 0.;
      for (Index itq = 1; itq < nzcolQ; ++itq) sqrNorm += numext::abs2(tval(Qidx(itq)));
      if(sqrNorm == RealScalar(0) && numext::imag(c0) == RealScalar(0))
      {
        beta = numext::real(c0);
        tval(Qidx(0)) = 1;
      }
      else
      {
        using std::sqrt;
        beta = sqrt(numext::abs2(c0) + sqrNorm);
        if(numext::real(c0) >= RealScalar(0))
          beta = -beta;
        tval(Qidx(0)) = 1;
        for (Index itq = 1; itq < nzcolQ; ++itq)
          tval(Qidx(itq)) /= (c0 - beta);
        tau = numext::conj((beta-c0) / beta);
          
      }
    }

    // Insert values in R
    for (Index  i = nzcolR-1; i >= 0; i--)
    {
      Index curIdx = Ridx(i);
      if(curIdx < nonzeroCol) 
      {
        m_R.insertBackByOuterInnerUnordered(col, curIdx) = tval(curIdx);
        tval(curIdx) = Scalar(0.);
      }
    }

    if(nonzeroCol < diagSize && abs(beta) >= pivotThreshold)
    {
      m_R.insertBackByOuterInner(col, nonzeroCol) = beta;
      // The householder coefficient
      m_hcoeffs(nonzeroCol) = tau;
      // Record the householder reflections
      for (Index itq = 0; itq < nzcolQ; ++itq)
      {
        Index iQ = Qidx(itq);
        m_Q.insertBackByOuterInnerUnordered(nonzeroCol,iQ) = tval(iQ);
        tval(iQ) = Scalar(0.);
      }
      nonzeroCol++;
      if(nonzeroCol<diagSize)
        m_Q.startVec(nonzeroCol);
    }
    else
    {
      // Zero pivot found: move implicitly this column to the end
      for (Index j = nonzeroCol; j < n-1; j++) 
        std::swap(m_pivotperm.indices()(j), m_pivotperm.indices()[j+1]);
      
      // Recompute the column elimination tree
      internal::coletree(m_pmat, m_etree, m_firstRowElt, m_pivotperm.indices().data());
      m_isEtreeOk = false;
    }
  }
  
  m_hcoeffs.tail(diagSize-nonzeroCol).setZero();
  
  // Finalize the column pointers of the sparse matrices R and Q
  m_Q.finalize();
  m_Q.makeCompressed();
  m_R.finalize();
  m_R.makeCompressed();
  m_isQSorted = false;

  m_nonzeropivots = nonzeroCol;
  
  if(nonzeroCol<n)
  {
    // Permute the triangular factor to put the 'dead' columns to the end
    QRMatrixType tempR(m_R);
    m_R = tempR * m_pivotperm;
    
    // Update the column permutation
    m_outputPerm_c = m_outputPerm_c * m_pivotperm;
  }
  
  m_isInitialized = true; 
  m_factorizationIsok = true;
  m_info = Success;
}
template<typename _MatrixType , typename _OrderingType >
ComputationInfo Eigen::SparseQR< _MatrixType, _OrderingType >::info ( ) const [inline]

Reports whether previous computation was successful.

Returns:
Success if computation was successful, NumericalIssue if the QR factorization reports a numerical problem InvalidInput if the input matrix is invalid
See also:
iparm()

Definition at line 255 of file SparseQR.h.

    {
      eigen_assert(m_isInitialized && "Decomposition is not initialized.");
      return m_info;
    }
template<typename _MatrixType , typename _OrderingType >
std::string Eigen::SparseQR< _MatrixType, _OrderingType >::lastErrorMessage ( ) const [inline]
Returns:
A string describing the type of error. This method is provided to ease debugging, not to handle errors.

Definition at line 188 of file SparseQR.h.

{ return m_lastError; }
template<typename _MatrixType , typename _OrderingType >
SparseQRMatrixQReturnType<SparseQR> Eigen::SparseQR< _MatrixType, _OrderingType >::matrixQ ( void  ) const [inline]
Returns:
an expression of the matrix Q as products of sparse Householder reflectors. The common usage of this function is to apply it to a dense matrix or vector 
 VectorXd B1, B2;
 // Initialize B1
 B2 = matrixQ() * B1;

To get a plain SparseMatrix representation of Q: 

 SparseMatrix<double> Q;
 Q = SparseQR<SparseMatrix<double> >(A).matrixQ();

Internally, this call simply performs a sparse product between the matrix Q and a sparse identity matrix. However, due to the fact that the sparse reflectors are stored unsorted, two transpositions are needed to sort them before performing the product.

Definition at line 173 of file SparseQR.h.

    { return SparseQRMatrixQReturnType<SparseQR>(*this); }
template<typename _MatrixType , typename _OrderingType >
const QRMatrixType& Eigen::SparseQR< _MatrixType, _OrderingType >::matrixR ( ) const [inline]
Returns:
a const reference to the sparse upper triangular matrix R of the QR factorization.
Warning:
The entries of the returned matrix are not sorted. This means that using it in algorithms expecting sorted entries will fail. This include random coefficient accesses (SpaseMatrix::coeff()), and coefficient-wise operations. Matrix products and triangular solves are fine though.

To sort the entries, you can assign it to a row-major matrix, and if a column-major matrix is required, you can copy it again: 

 SparseMatrix<double>          R  = qr.matrixR();  // column-major, not sorted!
 SparseMatrix<double,RowMajor> Rr = qr.matrixR();  // row-major, sorted
 SparseMatrix<double>          Rc = Rr;            // column-major, sorted

Definition at line 143 of file SparseQR.h.

{ return m_R; }
template<typename _MatrixType , typename _OrderingType >
Index Eigen::SparseQR< _MatrixType, _OrderingType >::rank ( ) const [inline]
Returns:
the number of non linearly dependent columns as determined by the pivoting threshold.
See also:
setPivotThreshold()

Definition at line 149 of file SparseQR.h.

    {
      eigen_assert(m_isInitialized && "The factorization should be called first, use compute()");
      return m_nonzeropivots; 
    }
template<typename _MatrixType , typename _OrderingType >
Index Eigen::SparseQR< _MatrixType, _OrderingType >::rows ( void  ) const [inline]
Returns:
the number of rows of the represented matrix.

Definition at line 124 of file SparseQR.h.

{ return m_pmat.rows(); }
template<typename _MatrixType , typename _OrderingType >
void Eigen::SparseQR< _MatrixType, _OrderingType >::setPivotThreshold ( const RealScalar &  threshold) [inline]

Sets the threshold that is used to determine linearly dependent columns during the factorization.

In practice, if during the factorization the norm of the column that has to be eliminated is below this threshold, then the entire column is treated as zero, and it is moved at the end.

Definition at line 222 of file SparseQR.h.

    {
      m_useDefaultThreshold = false;
      m_threshold = threshold;
    }
template<typename _MatrixType , typename _OrderingType >
template<typename Rhs >
const Solve<SparseQR, Rhs> Eigen::SparseQR< _MatrixType, _OrderingType >::solve ( const MatrixBase< Rhs > &  B) const [inline]
Returns:
the solution X of $ A X = B $ using the current decomposition of A.
See also:
compute()

Reimplemented from Eigen::SparseSolverBase< SparseQR< _MatrixType, _OrderingType > >.

Definition at line 233 of file SparseQR.h.

    {
      eigen_assert(m_isInitialized && "The factorization should be called first, use compute()");
      eigen_assert(this->rows() == B.rows() && "SparseQR::solve() : invalid number of rows in the right hand side matrix");
      return Solve<SparseQR, Rhs>(*this, B.derived());
    }
template<typename _MatrixType , typename _OrderingType >
template<typename Rhs >
const Solve<SparseQR, Rhs> Eigen::SparseQR< _MatrixType, _OrderingType >::solve ( const SparseMatrixBase< Rhs > &  b) const [inline]
Returns:
an expression of the solution x of $ A x = b $ using the current decomposition of A.
See also:
compute()

Reimplemented from Eigen::SparseSolverBase< SparseQR< _MatrixType, _OrderingType > >.

Definition at line 240 of file SparseQR.h.

    {
          eigen_assert(m_isInitialized && "The factorization should be called first, use compute()");
          eigen_assert(this->rows() == B.rows() && "SparseQR::solve() : invalid number of rows in the right hand side matrix");
          return Solve<SparseQR, Rhs>(*this, B.derived());
    }

Friends And Related Function Documentation

template<typename _MatrixType , typename _OrderingType >
friend struct SparseQR_QProduct [friend]

Definition at line 293 of file SparseQR.h.

Member Data Documentation

template<typename _MatrixType , typename _OrderingType >
bool Eigen::SparseQR< _MatrixType, _OrderingType >::m_analysisIsok [protected]

Definition at line 274 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
IndexVector Eigen::SparseQR< _MatrixType, _OrderingType >::m_etree [protected]

Definition at line 288 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
bool Eigen::SparseQR< _MatrixType, _OrderingType >::m_factorizationIsok [protected]

Definition at line 275 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
IndexVector Eigen::SparseQR< _MatrixType, _OrderingType >::m_firstRowElt [protected]

Definition at line 289 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
ScalarVector Eigen::SparseQR< _MatrixType, _OrderingType >::m_hcoeffs [protected]

Definition at line 281 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
ComputationInfo Eigen::SparseQR< _MatrixType, _OrderingType >::m_info [mutable, protected]

Definition at line 276 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
bool Eigen::SparseQR< _MatrixType, _OrderingType >::m_isEtreeOk [protected]

Definition at line 291 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
bool Eigen::SparseQR< _MatrixType, _OrderingType >::m_isQSorted [protected]

Definition at line 290 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
std::string Eigen::SparseQR< _MatrixType, _OrderingType >::m_lastError [protected]

Definition at line 277 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
Index Eigen::SparseQR< _MatrixType, _OrderingType >::m_nonzeropivots [protected]

Definition at line 287 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
PermutationType Eigen::SparseQR< _MatrixType, _OrderingType >::m_outputPerm_c [protected]

Definition at line 284 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
PermutationType Eigen::SparseQR< _MatrixType, _OrderingType >::m_perm_c [protected]

Definition at line 282 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
PermutationType Eigen::SparseQR< _MatrixType, _OrderingType >::m_pivotperm [protected]

Definition at line 283 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
QRMatrixType Eigen::SparseQR< _MatrixType, _OrderingType >::m_pmat [protected]

Definition at line 278 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
QRMatrixType Eigen::SparseQR< _MatrixType, _OrderingType >::m_Q [protected]

Definition at line 280 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
QRMatrixType Eigen::SparseQR< _MatrixType, _OrderingType >::m_R [protected]

Definition at line 279 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
RealScalar Eigen::SparseQR< _MatrixType, _OrderingType >::m_threshold [protected]

Definition at line 285 of file SparseQR.h.

template<typename _MatrixType , typename _OrderingType >
bool Eigen::SparseQR< _MatrixType, _OrderingType >::m_useDefaultThreshold [protected]

Definition at line 286 of file SparseQR.h.

The documentation for this class was generated from the following file:
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Defines