Performs a complex Schur decomposition of a real or complex square matrix. More...

#include <ComplexSchur.h>

Inheritance diagram for Eigen::ComplexSchur< _MatrixType >:

Collaboration diagram for Eigen::ComplexSchur< _MatrixType >:

Public Types
enum	{ RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, Options = MatrixType::Options, MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }
typedef _MatrixType	MatrixType
typedef MatrixType::Scalar	Scalar
	Scalar type for matrices of type `_MatrixType`.
typedef NumTraits< Scalar >::Real	RealScalar
typedef Eigen::Index	Index
typedef std::complex< RealScalar >	ComplexScalar
	Complex scalar type for `_MatrixType`.
typedef Matrix< ComplexScalar, RowsAtCompileTime, ColsAtCompileTime, Options, MaxRowsAtCompileTime, MaxColsAtCompileTime >	ComplexMatrixType
	Type for the matrices in the Schur decomposition.
Public Member Functions
	ComplexSchur (Index size=RowsAtCompileTime==Dynamic?1:RowsAtCompileTime)
	Default constructor.
template<typename InputType >
	ComplexSchur (const EigenBase< InputType > &matrix, bool computeU=true)
	Constructor; computes Schur decomposition of given matrix.
const ComplexMatrixType &	matrixU () const
	Returns the unitary matrix in the Schur decomposition.
const ComplexMatrixType &	matrixT () const
	Returns the triangular matrix in the Schur decomposition.
template<typename InputType >
ComplexSchur &	compute (const EigenBase< InputType > &matrix, bool computeU=true)
	Computes Schur decomposition of given matrix.
template<typename HessMatrixType , typename OrthMatrixType >
ComplexSchur &	computeFromHessenberg (const HessMatrixType &matrixH, const OrthMatrixType &matrixQ, bool computeU=true)
	Compute Schur decomposition from a given Hessenberg matrix.
ComputationInfo	info () const
	Reports whether previous computation was successful.
ComplexSchur &	setMaxIterations (Index maxIters)
	Sets the maximum number of iterations allowed.
Index	getMaxIterations ()
	Returns the maximum number of iterations.
Static Public Attributes
static const int	m_maxIterationsPerRow = 30
	Maximum number of iterations per row.
Protected Attributes
ComplexMatrixType	m_matT
ComplexMatrixType	m_matU
HessenbergDecomposition < MatrixType >	m_hess
ComputationInfo	m_info
bool	m_isInitialized
bool	m_matUisUptodate
Index	m_maxIters
Private Member Functions
bool	subdiagonalEntryIsNeglegible (Index i)
ComplexScalar	computeShift (Index iu, Index iter)
void	reduceToTriangularForm (bool computeU)
Friends
struct	internal::complex_schur_reduce_to_hessenberg< MatrixType, NumTraits< Scalar >::IsComplex >

Detailed Description

template<typename _MatrixType>
class Eigen::ComplexSchur< _MatrixType >

Performs a complex Schur decomposition of a real or complex square matrix.

Template Parameters:

_MatrixType the type of the matrix of which we are computing the Schur decomposition; this is expected to be an instantiation of the Matrix class template.

Given a real or complex square matrix A, this class computes the Schur decomposition: 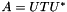$ A = U T U^*$ where U is a unitary complex matrix, and T is a complex upper triangular matrix. The diagonal of the matrix T corresponds to the eigenvalues of the matrix A.

Call the function compute() to compute the Schur decomposition of a given matrix. Alternatively, you can use the ComplexSchur(const MatrixType&, bool) constructor which computes the Schur decomposition at construction time. Once the decomposition is computed, you can use the matrixU() and matrixT() functions to retrieve the matrices U and V in the decomposition.

Note:: This code is inspired from Jampack

See also:: class RealSchur, class EigenSolver, class ComplexEigenSolver

Definition at line 51 of file ComplexSchur.h.

Member Typedef Documentation

template<typename _MatrixType>

typedef Matrix<ComplexScalar, RowsAtCompileTime, ColsAtCompileTime, Options, MaxRowsAtCompileTime, MaxColsAtCompileTime> Eigen::ComplexSchur< _MatrixType >::ComplexMatrixType

Type for the matrices in the Schur decomposition.

This is a square matrix with entries of type ComplexScalar. The size is the same as the size of _MatrixType.

Definition at line 81 of file ComplexSchur.h.

template<typename _MatrixType>

typedef std::complex<RealScalar> Eigen::ComplexSchur< _MatrixType >::ComplexScalar

Complex scalar type for _MatrixType.

This is std::complex<Scalar> if Scalar is real (e.g., float or double) and just Scalar if Scalar is complex.

Definition at line 74 of file ComplexSchur.h.

template<typename _MatrixType>

typedef Eigen::Index Eigen::ComplexSchur< _MatrixType >::Index

Deprecated:: since Eigen 3.3

Definition at line 66 of file ComplexSchur.h.

template<typename _MatrixType>

typedef _MatrixType Eigen::ComplexSchur< _MatrixType >::MatrixType

Definition at line 54 of file ComplexSchur.h.

template<typename _MatrixType>

typedef NumTraits<Scalar>::Real Eigen::ComplexSchur< _MatrixType >::RealScalar

Definition at line 65 of file ComplexSchur.h.

template<typename _MatrixType>

typedef MatrixType::Scalar Eigen::ComplexSchur< _MatrixType >::Scalar

Scalar type for matrices of type _MatrixType.

Definition at line 64 of file ComplexSchur.h.

Member Enumeration Documentation

template<typename _MatrixType>

anonymous enum

Enumerator:

RowsAtCompileTime
ColsAtCompileTime
Options
MaxRowsAtCompileTime
MaxColsAtCompileTime

Definition at line 55 of file ComplexSchur.h.

         {
      RowsAtCompileTime = MatrixType::RowsAtCompileTime,
      ColsAtCompileTime = MatrixType::ColsAtCompileTime,
      Options = MatrixType::Options,
      MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime,
      MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime
    };

Constructor & Destructor Documentation

template<typename _MatrixType>

Eigen::ComplexSchur< _MatrixType >::ComplexSchur ( Index size = RowsAtCompileTime==Dynamic ? 1 : RowsAtCompileTime ) [inline, explicit]

Default constructor.

Parameters:

[in] size Positive integer, size of the matrix whose Schur decomposition will be computed.

The default constructor is useful in cases in which the user intends to perform decompositions via compute(). The size parameter is only used as a hint. It is not an error to give a wrong size, but it may impair performance.

See also:: compute() for an example.

Definition at line 94 of file ComplexSchur.h.

                                                                      : RowsAtCompileTime)
      : m_matT(size,size),
        m_matU(size,size),
        m_hess(size),
        m_isInitialized(false),
        m_matUisUptodate(false),
        m_maxIters(-1)
    {}

template<typename _MatrixType>

template<typename InputType >

Eigen::ComplexSchur< _MatrixType >::ComplexSchur	(	const EigenBase< InputType > &	matrix,
		bool	computeU = `true`
	)		`[inline, explicit]`

Constructor; computes Schur decomposition of given matrix.

Parameters:

[in]	matrix	Square matrix whose Schur decomposition is to be computed.
[in]	computeU	If true, both T and U are computed; if false, only T is computed.

This constructor calls compute() to compute the Schur decomposition.

See also:: matrixT() and matrixU() for examples.

Definition at line 113 of file ComplexSchur.h.

      : m_matT(matrix.rows(),matrix.cols()),
        m_matU(matrix.rows(),matrix.cols()),
        m_hess(matrix.rows()),
        m_isInitialized(false),
        m_matUisUptodate(false),
        m_maxIters(-1)
    {
      compute(matrix.derived(), computeU);
    }

Member Function Documentation

template<typename MatrixType >

template<typename InputType >

ComplexSchur< MatrixType > & Eigen::ComplexSchur< MatrixType >::compute	(	const EigenBase< InputType > &	matrix,
		bool	computeU = `true`
	)

Computes Schur decomposition of given matrix.

Parameters:

[in]	matrix	Square matrix whose Schur decomposition is to be computed.
[in]	computeU	If true, both T and U are computed; if false, only T is computed.

Returns:: Reference to *this

The Schur decomposition is computed by first reducing the matrix to Hessenberg form using the class HessenbergDecomposition. The Hessenberg matrix is then reduced to triangular form by performing QR iterations with a single shift. The cost of computing the Schur decomposition depends on the number of iterations; as a rough guide, it may be taken on the number of iterations; as a rough guide, it may be taken to be 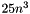$25n^3$ complex flops, or 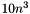$10n^3$ complex flops if computeU is false.

Example:

Output:

See also:: compute(const MatrixType&, bool, Index)

Definition at line 319 of file ComplexSchur.h.

{
  m_matUisUptodate = false;
  eigen_assert(matrix.cols() == matrix.rows());

  if(matrix.cols() == 1)
  {
    m_matT = matrix.derived().template cast<ComplexScalar>();
    if(computeU)  m_matU = ComplexMatrixType::Identity(1,1);
    m_info = Success;
    m_isInitialized = true;
    m_matUisUptodate = computeU;
    return *this;
  }

  internal::complex_schur_reduce_to_hessenberg<MatrixType, NumTraits<Scalar>::IsComplex>::run(*this, matrix.derived(), computeU);
  computeFromHessenberg(m_matT, m_matU, computeU);
  return *this;
}

template<typename MatrixType >

template<typename HessMatrixType , typename OrthMatrixType >

ComplexSchur< MatrixType > & Eigen::ComplexSchur< MatrixType >::computeFromHessenberg	(	const HessMatrixType &	matrixH,
		const OrthMatrixType &	matrixQ,
		bool	computeU = `true`
	)

Compute Schur decomposition from a given Hessenberg matrix.

Parameters:

[in]	matrixH	Matrix in Hessenberg form H
[in]	matrixQ	orthogonal matrix Q that transform a matrix A to H : A = Q H Q^T
	computeU	Computes the matriX U of the Schur vectors

Returns:: Reference to *this

This routine assumes that the matrix is already reduced in Hessenberg form matrixH using either the class HessenbergDecomposition or another mean. It computes the upper quasi-triangular matrix T of the Schur decomposition of H When computeU is true, this routine computes the matrix U such that A = U T U^T = (QZ) T (QZ)^T = Q H Q^T where A is the initial matrix

NOTE Q is referenced if computeU is true; so, if the initial orthogonal matrix is not available, the user should give an identity matrix (Q.setIdentity())

See also:: compute(const MatrixType&, bool)

Definition at line 341 of file ComplexSchur.h.

{
  m_matT = matrixH;
  if(computeU)
    m_matU = matrixQ;
  reduceToTriangularForm(computeU);
  return *this;
}

template<typename MatrixType >

ComplexSchur< MatrixType >::ComplexScalar Eigen::ComplexSchur< MatrixType >::computeShift	(	Index	iu,
		Index	iter
	)		`[private]`

Compute the shift in the current QR iteration.

Definition at line 281 of file ComplexSchur.h.

{
  using std::abs;
  if (iter == 10 || iter == 20) 
  {
    // exceptional shift, taken from http://www.netlib.org/eispack/comqr.f
    return abs(numext::real(m_matT.coeff(iu,iu-1))) + abs(numext::real(m_matT.coeff(iu-1,iu-2)));
  }

  // compute the shift as one of the eigenvalues of t, the 2x2
  // diagonal block on the bottom of the active submatrix
  Matrix<ComplexScalar,2,2> t = m_matT.template block<2,2>(iu-1,iu-1);
  RealScalar normt = t.cwiseAbs().sum();
  t /= normt;     // the normalization by sf is to avoid under/overflow

  ComplexScalar b = t.coeff(0,1) * t.coeff(1,0);
  ComplexScalar c = t.coeff(0,0) - t.coeff(1,1);
  ComplexScalar disc = sqrt(c*c + RealScalar(4)*b);
  ComplexScalar det = t.coeff(0,0) * t.coeff(1,1) - b;
  ComplexScalar trace = t.coeff(0,0) + t.coeff(1,1);
  ComplexScalar eival1 = (trace + disc) / RealScalar(2);
  ComplexScalar eival2 = (trace - disc) / RealScalar(2);

  if(numext::norm1(eival1) > numext::norm1(eival2))
    eival2 = det / eival1;
  else
    eival1 = det / eival2;

  // choose the eigenvalue closest to the bottom entry of the diagonal
  if(numext::norm1(eival1-t.coeff(1,1)) < numext::norm1(eival2-t.coeff(1,1)))
    return normt * eival1;
  else
    return normt * eival2;
}

template<typename _MatrixType>

Index Eigen::ComplexSchur< _MatrixType >::getMaxIterations ( ) [inline]

Returns the maximum number of iterations.

Definition at line 235 of file ComplexSchur.h.

    {
      return m_maxIters;
    }

template<typename _MatrixType>

ComputationInfo Eigen::ComplexSchur< _MatrixType >::info ( ) const [inline]

Reports whether previous computation was successful.

Returns:: Success if computation was succesful, NoConvergence otherwise.

Definition at line 217 of file ComplexSchur.h.

    {
      eigen_assert(m_isInitialized && "ComplexSchur is not initialized.");
      return m_info;
    }

template<typename _MatrixType>

const ComplexMatrixType& Eigen::ComplexSchur< _MatrixType >::matrixT ( ) const [inline]

Returns the triangular matrix in the Schur decomposition.

Returns:: A const reference to the matrix T.

It is assumed that either the constructor ComplexSchur(const MatrixType& matrix, bool computeU) or the member function compute(const MatrixType& matrix, bool computeU) has been called before to compute the Schur decomposition of a matrix.

Note that this function returns a plain square matrix. If you want to reference only the upper triangular part, use:

 schur.matrixT().triangularView<Upper>()

Example:

Output:

Definition at line 162 of file ComplexSchur.h.

    {
      eigen_assert(m_isInitialized && "ComplexSchur is not initialized.");
      return m_matT;
    }

template<typename _MatrixType>

const ComplexMatrixType& Eigen::ComplexSchur< _MatrixType >::matrixU ( ) const [inline]

Returns the unitary matrix in the Schur decomposition.

Returns:: A const reference to the matrix U.

It is assumed that either the constructor ComplexSchur(const MatrixType& matrix, bool computeU) or the member function compute(const MatrixType& matrix, bool computeU) has been called before to compute the Schur decomposition of a matrix, and that computeU was set to true (the default value).

Example:

Output:

Definition at line 138 of file ComplexSchur.h.

    {
      eigen_assert(m_isInitialized && "ComplexSchur is not initialized.");
      eigen_assert(m_matUisUptodate && "The matrix U has not been computed during the ComplexSchur decomposition.");
      return m_matU;
    }

template<typename MatrixType >

void Eigen::ComplexSchur< MatrixType >::reduceToTriangularForm ( bool computeU ) [private]

Definition at line 387 of file ComplexSchur.h.

{  
  Index maxIters = m_maxIters;
  if (maxIters == -1)
    maxIters = m_maxIterationsPerRow * m_matT.rows();

  // The matrix m_matT is divided in three parts. 
  // Rows 0,...,il-1 are decoupled from the rest because m_matT(il,il-1) is zero. 
  // Rows il,...,iu is the part we are working on (the active submatrix).
  // Rows iu+1,...,end are already brought in triangular form.
  Index iu = m_matT.cols() - 1;
  Index il;
  Index iter = 0; // number of iterations we are working on the (iu,iu) element
  Index totalIter = 0; // number of iterations for whole matrix

  while(true)
  {
    // find iu, the bottom row of the active submatrix
    while(iu > 0)
    {
      if(!subdiagonalEntryIsNeglegible(iu-1)) break;
      iter = 0;
      --iu;
    }

    // if iu is zero then we are done; the whole matrix is triangularized
    if(iu==0) break;

    // if we spent too many iterations, we give up
    iter++;
    totalIter++;
    if(totalIter > maxIters) break;

    // find il, the top row of the active submatrix
    il = iu-1;
    while(il > 0 && !subdiagonalEntryIsNeglegible(il-1))
    {
      --il;
    }

    /* perform the QR step using Givens rotations. The first rotation
       creates a bulge; the (il+2,il) element becomes nonzero. This
       bulge is chased down to the bottom of the active submatrix. */

    ComplexScalar shift = computeShift(iu, iter);
    JacobiRotation<ComplexScalar> rot;
    rot.makeGivens(m_matT.coeff(il,il) - shift, m_matT.coeff(il+1,il));
    m_matT.rightCols(m_matT.cols()-il).applyOnTheLeft(il, il+1, rot.adjoint());
    m_matT.topRows((std::min)(il+2,iu)+1).applyOnTheRight(il, il+1, rot);
    if(computeU) m_matU.applyOnTheRight(il, il+1, rot);

    for(Index i=il+1 ; i<iu ; i++)
    {
      rot.makeGivens(m_matT.coeffRef(i,i-1), m_matT.coeffRef(i+1,i-1), &m_matT.coeffRef(i,i-1));
      m_matT.coeffRef(i+1,i-1) = ComplexScalar(0);
      m_matT.rightCols(m_matT.cols()-i).applyOnTheLeft(i, i+1, rot.adjoint());
      m_matT.topRows((std::min)(i+2,iu)+1).applyOnTheRight(i, i+1, rot);
      if(computeU) m_matU.applyOnTheRight(i, i+1, rot);
    }
  }

  if(totalIter <= maxIters)
    m_info = Success;
  else
    m_info = NoConvergence;

  m_isInitialized = true;
  m_matUisUptodate = computeU;
}

template<typename _MatrixType>

ComplexSchur& Eigen::ComplexSchur< _MatrixType >::setMaxIterations ( Index maxIters ) [inline]

Sets the maximum number of iterations allowed.

If not specified by the user, the maximum number of iterations is m_maxIterationsPerRow times the size of the matrix.

Definition at line 228 of file ComplexSchur.h.

    {
      m_maxIters = maxIters;
      return *this;
    }

template<typename MatrixType >

bool Eigen::ComplexSchur< MatrixType >::subdiagonalEntryIsNeglegible ( Index i ) [inline, private]

If m_matT(i+1,i) is neglegible in floating point arithmetic compared to m_matT(i,i) and m_matT(j,j), then set it to zero and return true, else return false.

Definition at line 266 of file ComplexSchur.h.

{
  RealScalar d = numext::norm1(m_matT.coeff(i,i)) + numext::norm1(m_matT.coeff(i+1,i+1));
  RealScalar sd = numext::norm1(m_matT.coeff(i+1,i));
  if (internal::isMuchSmallerThan(sd, d, NumTraits<RealScalar>::epsilon()))
  {
    m_matT.coeffRef(i+1,i) = ComplexScalar(0);
    return true;
  }
  return false;
}

Friends And Related Function Documentation

template<typename _MatrixType>

friend struct internal::complex_schur_reduce_to_hessenberg< MatrixType, NumTraits< Scalar >::IsComplex > [friend]

Definition at line 259 of file ComplexSchur.h.

Member Data Documentation

template<typename _MatrixType>

HessenbergDecomposition<MatrixType> Eigen::ComplexSchur< _MatrixType >::m_hess [protected]

Definition at line 249 of file ComplexSchur.h.

template<typename _MatrixType>

ComputationInfo Eigen::ComplexSchur< _MatrixType >::m_info [protected]

Definition at line 250 of file ComplexSchur.h.

template<typename _MatrixType>

bool Eigen::ComplexSchur< _MatrixType >::m_isInitialized [protected]

Definition at line 251 of file ComplexSchur.h.

template<typename _MatrixType>

ComplexMatrixType Eigen::ComplexSchur< _MatrixType >::m_matT [protected]

Definition at line 248 of file ComplexSchur.h.

template<typename _MatrixType>

ComplexMatrixType Eigen::ComplexSchur< _MatrixType >::m_matU [protected]

Definition at line 248 of file ComplexSchur.h.

template<typename _MatrixType>

bool Eigen::ComplexSchur< _MatrixType >::m_matUisUptodate [protected]

Definition at line 252 of file ComplexSchur.h.

template<typename _MatrixType>

const int Eigen::ComplexSchur< _MatrixType >::m_maxIterationsPerRow = 30 [static]

Maximum number of iterations per row.

If not otherwise specified, the maximum number of iterations is this number times the size of the matrix. It is currently set to 30.

Definition at line 245 of file ComplexSchur.h.

template<typename _MatrixType>

Index Eigen::ComplexSchur< _MatrixType >::m_maxIters [protected]

Definition at line 253 of file ComplexSchur.h.

The documentation for this class was generated from the following file:

ComplexSchur.h

Public Types

Public Member Functions

Static Public Attributes

Protected Attributes

Private Member Functions

Friends

Detailed Description

template<typename _MatrixType> class Eigen::ComplexSchur< _MatrixType >

Member Typedef Documentation

Member Enumeration Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Member Data Documentation

template<typename _MatrixType>
class Eigen::ComplexSchur< _MatrixType >