Computes eigenvalues and eigenvectors of general complex matrices. More...

#include <ComplexEigenSolver.h>

Collaboration diagram for Eigen::ComplexEigenSolver< _MatrixType >:

Public Types
enum	{ RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, Options = MatrixType::Options, MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }
typedef _MatrixType	MatrixType
	Synonym for the template parameter `_MatrixType`.
typedef MatrixType::Scalar	Scalar
	Scalar type for matrices of type MatrixType.
typedef NumTraits< Scalar >::Real	RealScalar
typedef Eigen::Index	Index
typedef std::complex< RealScalar >	ComplexScalar
	Complex scalar type for MatrixType.
typedef Matrix< ComplexScalar, ColsAtCompileTime, 1, Options &(~RowMajor), MaxColsAtCompileTime, 1 >	EigenvalueType
	Type for vector of eigenvalues as returned by eigenvalues().
typedef Matrix< ComplexScalar, RowsAtCompileTime, ColsAtCompileTime, Options, MaxRowsAtCompileTime, MaxColsAtCompileTime >	EigenvectorType
	Type for matrix of eigenvectors as returned by eigenvectors().
Public Member Functions
	ComplexEigenSolver ()
	Default constructor.
	ComplexEigenSolver (Index size)
	Default Constructor with memory preallocation.
template<typename InputType >
	ComplexEigenSolver (const EigenBase< InputType > &matrix, bool computeEigenvectors=true)
	Constructor; computes eigendecomposition of given matrix.
const EigenvectorType &	eigenvectors () const
	Returns the eigenvectors of given matrix.
const EigenvalueType &	eigenvalues () const
	Returns the eigenvalues of given matrix.
template<typename InputType >
ComplexEigenSolver &	compute (const EigenBase< InputType > &matrix, bool computeEigenvectors=true)
	Computes eigendecomposition of given matrix.
ComputationInfo	info () const
	Reports whether previous computation was successful.
ComplexEigenSolver &	setMaxIterations (Index maxIters)
	Sets the maximum number of iterations allowed.
Index	getMaxIterations ()
	Returns the maximum number of iterations.
Static Protected Member Functions
static void	check_template_parameters ()
Protected Attributes
EigenvectorType	m_eivec
EigenvalueType	m_eivalues
ComplexSchur< MatrixType >	m_schur
bool	m_isInitialized
bool	m_eigenvectorsOk
EigenvectorType	m_matX
Private Member Functions
void	doComputeEigenvectors (const RealScalar &matrixnorm)
void	sortEigenvalues (bool computeEigenvectors)

Detailed Description

template<typename _MatrixType>
class Eigen::ComplexEigenSolver< _MatrixType >

Computes eigenvalues and eigenvectors of general complex matrices.

Template Parameters:

_MatrixType the type of the matrix of which we are computing the eigendecomposition; this is expected to be an instantiation of the Matrix class template.

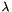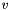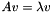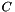The eigenvalues and eigenvectors of a matrix $ A $ are scalars $\lambda$ and vectors $ v $ such that $Av = \lambda v$ . If $ D $ is a diagonal matrix with the eigenvalues on the diagonal, and 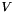$ V $ is a matrix with the eigenvectors as its columns, then 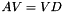$ A V = V D $ . The matrix 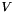$ V $ is almost always invertible, in which case we have 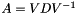$A = V D V^{-1}$ . This is called the eigendecomposition.

The main function in this class is compute(), which computes the eigenvalues and eigenvectors of a given function. The documentation for that function contains an example showing the main features of the class.

See also:: class EigenSolver, class SelfAdjointEigenSolver

Definition at line 45 of file ComplexEigenSolver.h.

Member Typedef Documentation

template<typename _MatrixType>

typedef std::complex<RealScalar> Eigen::ComplexEigenSolver< _MatrixType >::ComplexScalar

Complex scalar type for MatrixType.

This is std::complex<Scalar> if Scalar is real (e.g., float or double) and just Scalar if Scalar is complex.

Definition at line 71 of file ComplexEigenSolver.h.

template<typename _MatrixType>

typedef Matrix<ComplexScalar, ColsAtCompileTime, 1, Options&(~RowMajor), MaxColsAtCompileTime, 1> Eigen::ComplexEigenSolver< _MatrixType >::EigenvalueType

Type for vector of eigenvalues as returned by eigenvalues().

This is a column vector with entries of type ComplexScalar. The length of the vector is the size of MatrixType.

Definition at line 78 of file ComplexEigenSolver.h.

template<typename _MatrixType>

typedef Matrix<ComplexScalar, RowsAtCompileTime, ColsAtCompileTime, Options, MaxRowsAtCompileTime, MaxColsAtCompileTime> Eigen::ComplexEigenSolver< _MatrixType >::EigenvectorType

Type for matrix of eigenvectors as returned by eigenvectors().

This is a square matrix with entries of type ComplexScalar. The size is the same as the size of MatrixType.

Definition at line 85 of file ComplexEigenSolver.h.

template<typename _MatrixType>

typedef Eigen::Index Eigen::ComplexEigenSolver< _MatrixType >::Index

Deprecated:: since Eigen 3.3

Definition at line 63 of file ComplexEigenSolver.h.

template<typename _MatrixType>

typedef _MatrixType Eigen::ComplexEigenSolver< _MatrixType >::MatrixType

Synonym for the template parameter _MatrixType.

Definition at line 50 of file ComplexEigenSolver.h.

template<typename _MatrixType>

typedef NumTraits<Scalar>::Real Eigen::ComplexEigenSolver< _MatrixType >::RealScalar

Definition at line 62 of file ComplexEigenSolver.h.

template<typename _MatrixType>

typedef MatrixType::Scalar Eigen::ComplexEigenSolver< _MatrixType >::Scalar

Scalar type for matrices of type MatrixType.

Definition at line 61 of file ComplexEigenSolver.h.

Member Enumeration Documentation

template<typename _MatrixType>

anonymous enum

Enumerator:

RowsAtCompileTime
ColsAtCompileTime
Options
MaxRowsAtCompileTime
MaxColsAtCompileTime

Definition at line 52 of file ComplexEigenSolver.h.

         {
      RowsAtCompileTime = MatrixType::RowsAtCompileTime,
      ColsAtCompileTime = MatrixType::ColsAtCompileTime,
      Options = MatrixType::Options,
      MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime,
      MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime
    };

Constructor & Destructor Documentation

template<typename _MatrixType>

Eigen::ComplexEigenSolver< _MatrixType >::ComplexEigenSolver ( ) [inline]

Default constructor.

The default constructor is useful in cases in which the user intends to perform decompositions via compute().

Definition at line 92 of file ComplexEigenSolver.h.

            : m_eivec(),
              m_eivalues(),
              m_schur(),
              m_isInitialized(false),
              m_eigenvectorsOk(false),
              m_matX()
    {}

template<typename _MatrixType>

Eigen::ComplexEigenSolver< _MatrixType >::ComplexEigenSolver ( Index size ) [inline, explicit]

Default Constructor with memory preallocation.

Like the default constructor but with preallocation of the internal data according to the specified problem size.

See also:: ComplexEigenSolver()

Definition at line 107 of file ComplexEigenSolver.h.

            : m_eivec(size, size),
              m_eivalues(size),
              m_schur(size),
              m_isInitialized(false),
              m_eigenvectorsOk(false),
              m_matX(size, size)
    {}

template<typename _MatrixType>

template<typename InputType >

Eigen::ComplexEigenSolver< _MatrixType >::ComplexEigenSolver	(	const EigenBase< InputType > &	matrix,
		bool	computeEigenvectors = `true`
	)		`[inline, explicit]`

Constructor; computes eigendecomposition of given matrix.

Parameters:

[in]	matrix	Square matrix whose eigendecomposition is to be computed.
[in]	computeEigenvectors	If true, both the eigenvectors and the eigenvalues are computed; if false, only the eigenvalues are computed.

This constructor calls compute() to compute the eigendecomposition.

Definition at line 126 of file ComplexEigenSolver.h.

            : m_eivec(matrix.rows(),matrix.cols()),
              m_eivalues(matrix.cols()),
              m_schur(matrix.rows()),
              m_isInitialized(false),
              m_eigenvectorsOk(false),
              m_matX(matrix.rows(),matrix.cols())
    {
      compute(matrix.derived(), computeEigenvectors);
    }

Member Function Documentation

template<typename _MatrixType>

static void Eigen::ComplexEigenSolver< _MatrixType >::check_template_parameters ( ) [inline, static, protected]

Definition at line 240 of file ComplexEigenSolver.h.

    {
      EIGEN_STATIC_ASSERT_NON_INTEGER(Scalar);
    }

template<typename MatrixType >

template<typename InputType >

ComplexEigenSolver< MatrixType > & Eigen::ComplexEigenSolver< MatrixType >::compute	(	const EigenBase< InputType > &	matrix,
		bool	computeEigenvectors = `true`
	)

Computes eigendecomposition of given matrix.

Parameters:

[in]	matrix	Square matrix whose eigendecomposition is to be computed.
[in]	computeEigenvectors	If true, both the eigenvectors and the eigenvalues are computed; if false, only the eigenvalues are computed.

Returns:: Reference to *this

This function computes the eigenvalues of the complex matrix matrix. The eigenvalues() function can be used to retrieve them. If computeEigenvectors is true, then the eigenvectors are also computed and can be retrieved by calling eigenvectors().

The matrix is first reduced to Schur form using the ComplexSchur class. The Schur decomposition is then used to compute the eigenvalues and eigenvectors.

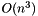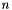The cost of the computation is dominated by the cost of the Schur decomposition, which is $ O(n^3) $ where $ n $ is the size of the matrix.

Example:

Output:

Definition at line 261 of file ComplexEigenSolver.h.

{
  check_template_parameters();
  
  // this code is inspired from Jampack
  eigen_assert(matrix.cols() == matrix.rows());

  // Do a complex Schur decomposition, A = U T U^*
  // The eigenvalues are on the diagonal of T.
  m_schur.compute(matrix.derived(), computeEigenvectors);

  if(m_schur.info() == Success)
  {
    m_eivalues = m_schur.matrixT().diagonal();
    if(computeEigenvectors)
      doComputeEigenvectors(m_schur.matrixT().norm());
    sortEigenvalues(computeEigenvectors);
  }

  m_isInitialized = true;
  m_eigenvectorsOk = computeEigenvectors;
  return *this;
}

template<typename MatrixType >

void Eigen::ComplexEigenSolver< MatrixType >::doComputeEigenvectors ( const RealScalar & matrixnorm ) [private]

Definition at line 287 of file ComplexEigenSolver.h.

{
  const Index n = m_eivalues.size();

  // Compute X such that T = X D X^(-1), where D is the diagonal of T.
  // The matrix X is unit triangular.
  m_matX = EigenvectorType::Zero(n, n);
  for(Index k=n-1 ; k>=0 ; k--)
  {
    m_matX.coeffRef(k,k) = ComplexScalar(1.0,0.0);
    // Compute X(i,k) using the (i,k) entry of the equation X T = D X
    for(Index i=k-1 ; i>=0 ; i--)
    {
      m_matX.coeffRef(i,k) = -m_schur.matrixT().coeff(i,k);
      if(k-i-1>0)
        m_matX.coeffRef(i,k) -= (m_schur.matrixT().row(i).segment(i+1,k-i-1) * m_matX.col(k).segment(i+1,k-i-1)).value();
      ComplexScalar z = m_schur.matrixT().coeff(i,i) - m_schur.matrixT().coeff(k,k);
      if(z==ComplexScalar(0))
      {
        // If the i-th and k-th eigenvalue are equal, then z equals 0.
        // Use a small value instead, to prevent division by zero.
        numext::real_ref(z) = NumTraits<RealScalar>::epsilon() * matrixnorm;
      }
      m_matX.coeffRef(i,k) = m_matX.coeff(i,k) / z;
    }
  }

  // Compute V as V = U X; now A = U T U^* = U X D X^(-1) U^* = V D V^(-1)
  m_eivec.noalias() = m_schur.matrixU() * m_matX;
  // .. and normalize the eigenvectors
  for(Index k=0 ; k<n ; k++)
  {
    m_eivec.col(k).normalize();
  }
}

template<typename _MatrixType>

const EigenvalueType& Eigen::ComplexEigenSolver< _MatrixType >::eigenvalues ( ) const [inline]

Returns the eigenvalues of given matrix.

Returns:: A const reference to the column vector containing the eigenvalues.

Precondition:: Either the constructor ComplexEigenSolver(const MatrixType& matrix, bool) or the member function compute(const MatrixType& matrix, bool) has been called before to compute the eigendecomposition of a matrix.

This function returns a column vector containing the eigenvalues. Eigenvalues are repeated according to their algebraic multiplicity, so there are as many eigenvalues as rows in the matrix. The eigenvalues are not sorted in any particular order.

Example:

Output:

Definition at line 182 of file ComplexEigenSolver.h.

    {
      eigen_assert(m_isInitialized && "ComplexEigenSolver is not initialized.");
      return m_eivalues;
    }

template<typename _MatrixType>

const EigenvectorType& Eigen::ComplexEigenSolver< _MatrixType >::eigenvectors ( ) const [inline]

Returns the eigenvectors of given matrix.

Returns:: A const reference to the matrix whose columns are the eigenvectors.

Precondition:: Either the constructor ComplexEigenSolver(const MatrixType& matrix, bool) or the member function compute(const MatrixType& matrix, bool) has been called before to compute the eigendecomposition of a matrix, and computeEigenvectors was set to true (the default).

This function returns a matrix whose columns are the eigenvectors. Column 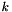$ k $ is an eigenvector corresponding to eigenvalue number 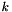$ k $ as returned by eigenvalues(). The eigenvectors are normalized to have (Euclidean) norm equal to one. The matrix returned by this function is the matrix 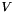$ V $ in the eigendecomposition 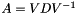$A = V D V^{-1}$ , if it exists.

Example:

Output:

Definition at line 157 of file ComplexEigenSolver.h.

    {
      eigen_assert(m_isInitialized && "ComplexEigenSolver is not initialized.");
      eigen_assert(m_eigenvectorsOk && "The eigenvectors have not been computed together with the eigenvalues.");
      return m_eivec;
    }

template<typename _MatrixType>

Index Eigen::ComplexEigenSolver< _MatrixType >::getMaxIterations ( ) [inline]

Returns the maximum number of iterations.

Definition at line 233 of file ComplexEigenSolver.h.

    {
      return m_schur.getMaxIterations();
    }

template<typename _MatrixType>

ComputationInfo Eigen::ComplexEigenSolver< _MatrixType >::info ( ) const [inline]

Reports whether previous computation was successful.

Returns:: Success if computation was succesful, NoConvergence otherwise.

Definition at line 219 of file ComplexEigenSolver.h.

    {
      eigen_assert(m_isInitialized && "ComplexEigenSolver is not initialized.");
      return m_schur.info();
    }

template<typename _MatrixType>

ComplexEigenSolver& Eigen::ComplexEigenSolver< _MatrixType >::setMaxIterations ( Index maxIters ) [inline]

Sets the maximum number of iterations allowed.

Definition at line 226 of file ComplexEigenSolver.h.

    {
      m_schur.setMaxIterations(maxIters);
      return *this;
    }

template<typename MatrixType >

void Eigen::ComplexEigenSolver< MatrixType >::sortEigenvalues ( bool computeEigenvectors ) [private]

Definition at line 325 of file ComplexEigenSolver.h.

{
  const Index n =  m_eivalues.size();
  for (Index i=0; i<n; i++)
  {
    Index k;
    m_eivalues.cwiseAbs().tail(n-i).minCoeff(&k);
    if (k != 0)
    {
      k += i;
      std::swap(m_eivalues[k],m_eivalues[i]);
      if(computeEigenvectors)
    m_eivec.col(i).swap(m_eivec.col(k));
    }
  }
}