Performs a real QZ decomposition of a pair of square matrices. More...

#include <RealQZ.h>

Inheritance diagram for Eigen::RealQZ< _MatrixType >:

Collaboration diagram for Eigen::RealQZ< _MatrixType >:

Public Types
enum	{ RowsAtCompileTime = MatrixType::RowsAtCompileTime, ColsAtCompileTime = MatrixType::ColsAtCompileTime, Options = MatrixType::Options, MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime, MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime }
typedef _MatrixType	MatrixType
typedef MatrixType::Scalar	Scalar
typedef std::complex< typename NumTraits< Scalar >::Real >	ComplexScalar
typedef Eigen::Index	Index
typedef Matrix< ComplexScalar, ColsAtCompileTime, 1, Options &~RowMajor, MaxColsAtCompileTime, 1 >	EigenvalueType
typedef Matrix< Scalar, ColsAtCompileTime, 1, Options &~RowMajor, MaxColsAtCompileTime, 1 >	ColumnVectorType
Public Member Functions
	RealQZ (Index size=RowsAtCompileTime==Dynamic?1:RowsAtCompileTime)
	Default constructor.
	RealQZ (const MatrixType &A, const MatrixType &B, bool computeQZ=true)
	Constructor; computes real QZ decomposition of given matrices.
const MatrixType &	matrixQ () const
	Returns matrix Q in the QZ decomposition.
const MatrixType &	matrixZ () const
	Returns matrix Z in the QZ decomposition.
const MatrixType &	matrixS () const
	Returns matrix S in the QZ decomposition.
const MatrixType &	matrixT () const
	Returns matrix S in the QZ decomposition.
RealQZ &	compute (const MatrixType &A, const MatrixType &B, bool computeQZ=true)
	Computes QZ decomposition of given matrix.
ComputationInfo	info () const
	Reports whether previous computation was successful.
Index	iterations () const
	Returns number of performed QR-like iterations.
RealQZ &	setMaxIterations (Index maxIters)
Private Types
typedef Matrix< Scalar, 3, 1 >	Vector3s
typedef Matrix< Scalar, 2, 1 >	Vector2s
typedef Matrix< Scalar, 2, 2 >	Matrix2s
typedef JacobiRotation< Scalar >	JRs
Private Member Functions
void	hessenbergTriangular ()
void	computeNorms ()
Index	findSmallSubdiagEntry (Index iu)
Index	findSmallDiagEntry (Index f, Index l)
void	splitOffTwoRows (Index i)
void	pushDownZero (Index z, Index f, Index l)
void	step (Index f, Index l, Index iter)
Private Attributes
MatrixType	m_S
MatrixType	m_T
MatrixType	m_Q
MatrixType	m_Z
Matrix< Scalar, Dynamic, 1 >	m_workspace
ComputationInfo	m_info
Index	m_maxIters
bool	m_isInitialized
bool	m_computeQZ
Scalar	m_normOfT
Scalar	m_normOfS
Index	m_global_iter

Detailed Description

template<typename _MatrixType>
class Eigen::RealQZ< _MatrixType >

Performs a real QZ decomposition of a pair of square matrices.

Template Parameters:

_MatrixType the type of the matrix of which we are computing the real QZ decomposition; this is expected to be an instantiation of the Matrix class template.

Given a real square matrices A and B, this class computes the real QZ decomposition: 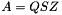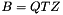$ A = Q S Z $ , $ B = Q T Z $ where Q and Z are real orthogonal matrixes, T is upper-triangular matrix, and S is upper quasi-triangular matrix. An orthogonal matrix is a matrix whose inverse is equal to its transpose, 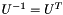$U^{-1} = U^T$ . A quasi-triangular matrix is a block-triangular matrix whose diagonal consists of 1-by-1 blocks and 2-by-2 blocks where further reduction is impossible due to complex eigenvalues.

The eigenvalues of the pencil 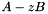$ A - z B $ can be obtained from 1x1 and 2x2 blocks on the diagonals of S and T.

Call the function compute() to compute the real QZ decomposition of a given pair of matrices. Alternatively, you can use the RealQZ(const MatrixType& B, const MatrixType& B, bool computeQZ) constructor which computes the real QZ decomposition at construction time. Once the decomposition is computed, you can use the matrixS(), matrixT(), matrixQ() and matrixZ() functions to retrieve the matrices S, T, Q and Z in the decomposition. If computeQZ==false, some time is saved by not computing matrices Q and Z.

Example:

Output:

Note:: The implementation is based on the algorithm in "Matrix Computations" by Gene H. Golub and Charles F. Van Loan, and a paper "An algorithm for generalized eigenvalue problems" by C.B.Moler and G.W.Stewart.

See also:: class RealSchur, class ComplexSchur, class EigenSolver, class ComplexEigenSolver

Definition at line 57 of file RealQZ.h.

Member Typedef Documentation

template<typename _MatrixType>

typedef Matrix<Scalar, ColsAtCompileTime, 1, Options & ~RowMajor, MaxColsAtCompileTime, 1> Eigen::RealQZ< _MatrixType >::ColumnVectorType

Definition at line 73 of file RealQZ.h.

template<typename _MatrixType>

typedef std::complex<typename NumTraits<Scalar>::Real> Eigen::RealQZ< _MatrixType >::ComplexScalar

Definition at line 69 of file RealQZ.h.

template<typename _MatrixType>

typedef Matrix<ComplexScalar, ColsAtCompileTime, 1, Options & ~RowMajor, MaxColsAtCompileTime, 1> Eigen::RealQZ< _MatrixType >::EigenvalueType

Definition at line 72 of file RealQZ.h.

template<typename _MatrixType>

typedef Eigen::Index Eigen::RealQZ< _MatrixType >::Index

Deprecated:: since Eigen 3.3

Definition at line 70 of file RealQZ.h.

template<typename _MatrixType>

typedef JacobiRotation<Scalar> Eigen::RealQZ< _MatrixType >::JRs [private]

Definition at line 203 of file RealQZ.h.

template<typename _MatrixType>

typedef Matrix<Scalar,2,2> Eigen::RealQZ< _MatrixType >::Matrix2s [private]

Definition at line 202 of file RealQZ.h.

template<typename _MatrixType>

typedef _MatrixType Eigen::RealQZ< _MatrixType >::MatrixType

Definition at line 60 of file RealQZ.h.

template<typename _MatrixType>

typedef MatrixType::Scalar Eigen::RealQZ< _MatrixType >::Scalar

Definition at line 68 of file RealQZ.h.

template<typename _MatrixType>

typedef Matrix<Scalar,2,1> Eigen::RealQZ< _MatrixType >::Vector2s [private]

Definition at line 201 of file RealQZ.h.

template<typename _MatrixType>

typedef Matrix<Scalar,3,1> Eigen::RealQZ< _MatrixType >::Vector3s [private]

Definition at line 200 of file RealQZ.h.

Member Enumeration Documentation

template<typename _MatrixType>

anonymous enum

Enumerator:

RowsAtCompileTime
ColsAtCompileTime
Options
MaxRowsAtCompileTime
MaxColsAtCompileTime

Definition at line 61 of file RealQZ.h.

           {
        RowsAtCompileTime = MatrixType::RowsAtCompileTime,
        ColsAtCompileTime = MatrixType::ColsAtCompileTime,
        Options = MatrixType::Options,
        MaxRowsAtCompileTime = MatrixType::MaxRowsAtCompileTime,
        MaxColsAtCompileTime = MatrixType::MaxColsAtCompileTime
      };

Constructor & Destructor Documentation

template<typename _MatrixType>

Eigen::RealQZ< _MatrixType >::RealQZ ( Index size = RowsAtCompileTime==Dynamic ? 1 : RowsAtCompileTime ) [inline, explicit]

Default constructor.

Parameters:

[in] size Positive integer, size of the matrix whose QZ decomposition will be computed.

The default constructor is useful in cases in which the user intends to perform decompositions via compute(). The size parameter is only used as a hint. It is not an error to give a wrong size, but it may impair performance.

See also:: compute() for an example.

Definition at line 86 of file RealQZ.h.

                                                                  : RowsAtCompileTime) :
        m_S(size, size),
        m_T(size, size),
        m_Q(size, size),
        m_Z(size, size),
        m_workspace(size*2),
        m_maxIters(400),
        m_isInitialized(false)
        { }

template<typename _MatrixType>

Eigen::RealQZ< _MatrixType >::RealQZ	(	const MatrixType &	A,
		const MatrixType &	B,
		bool	computeQZ = `true`
	)		`[inline]`

Constructor; computes real QZ decomposition of given matrices.

Parameters:

[in]	A	Matrix A.
[in]	B	Matrix B.
[in]	computeQZ	If false, A and Z are not computed.

This constructor calls compute() to compute the QZ decomposition.

Definition at line 104 of file RealQZ.h.

                                                                              :
        m_S(A.rows(),A.cols()),
        m_T(A.rows(),A.cols()),
        m_Q(A.rows(),A.cols()),
        m_Z(A.rows(),A.cols()),
        m_workspace(A.rows()*2),
        m_maxIters(400),
        m_isInitialized(false) {
          compute(A, B, computeQZ);
        }

Member Function Documentation

template<typename MatrixType >

RealQZ< MatrixType > & Eigen::RealQZ< MatrixType >::compute	(	const MatrixType &	A,
		const MatrixType &	B,
		bool	computeQZ = `true`
	)

Computes QZ decomposition of given matrix.

Parameters:

[in]	A	Matrix A.
[in]	B	Matrix B.
[in]	computeQZ	If false, A and Z are not computed.

Returns:: Reference to *this

Definition at line 557 of file RealQZ.h.

    {

      const Index dim = A_in.cols();

      eigen_assert (A_in.rows()==dim && A_in.cols()==dim 
          && B_in.rows()==dim && B_in.cols()==dim 
          && "Need square matrices of the same dimension");

      m_isInitialized = true;
      m_computeQZ = computeQZ;
      m_S = A_in; m_T = B_in;
      m_workspace.resize(dim*2);
      m_global_iter = 0;

      // entrance point: hessenberg triangular decomposition
      hessenbergTriangular();
      // compute L1 vector norms of T, S into m_normOfS, m_normOfT
      computeNorms();

      Index l = dim-1, 
            f, 
            local_iter = 0;

      while (l>0 && local_iter<m_maxIters)
      {
        f = findSmallSubdiagEntry(l);
        // now rows and columns f..l (including) decouple from the rest of the problem
        if (f>0) m_S.coeffRef(f,f-1) = Scalar(0.0);
        if (f == l) // One root found
        {
          l--;
          local_iter = 0;
        }
        else if (f == l-1) // Two roots found
        {
          splitOffTwoRows(f);
          l -= 2;
          local_iter = 0;
        }
        else // No convergence yet
        {
          // if there's zero on diagonal of T, we can isolate an eigenvalue with Givens rotations
          Index z = findSmallDiagEntry(f,l);
          if (z>=f)
          {
            // zero found
            pushDownZero(z,f,l);
          }
          else
          {
            // We are sure now that S.block(f,f, l-f+1,l-f+1) is underuced upper-Hessenberg 
            // and T.block(f,f, l-f+1,l-f+1) is invertible uper-triangular, which allows to
            // apply a QR-like iteration to rows and columns f..l.
            step(f,l, local_iter);
            local_iter++;
            m_global_iter++;
          }
        }
      }
      // check if we converged before reaching iterations limit
      m_info = (local_iter<m_maxIters) ? Success : NoConvergence;
      return *this;
    } // end compute

template<typename MatrixType >

void Eigen::RealQZ< MatrixType >::computeNorms ( ) [inline, private]

Computes vector L1 norms of S and T when in Hessenberg-Triangular form already

Definition at line 264 of file RealQZ.h.

    {
      const Index size = m_S.cols();
      m_normOfS = Scalar(0.0);
      m_normOfT = Scalar(0.0);
      for (Index j = 0; j < size; ++j)
      {
        m_normOfS += m_S.col(j).segment(0, (std::min)(size,j+2)).cwiseAbs().sum();
        m_normOfT += m_T.row(j).segment(j, size - j).cwiseAbs().sum();
      }
    }

template<typename MatrixType >

Index Eigen::RealQZ< MatrixType >::findSmallDiagEntry	(	Index	f,
		Index	l
	)		`[inline, private]`

Look for single small diagonal element T(res, res) for res between f and l, and return res (or f-1)

Definition at line 297 of file RealQZ.h.

    {
      using std::abs;
      Index res = l;
      while (res >= f) {
        if (abs(m_T.coeff(res,res)) <= NumTraits<Scalar>::epsilon() * m_normOfT)
          break;
        res--;
      }
      return res;
    }

template<typename MatrixType >

Index Eigen::RealQZ< MatrixType >::findSmallSubdiagEntry ( Index iu ) [inline, private]

Look for single small sub-diagonal element S(res, res-1) and return res (or 0)

Definition at line 279 of file RealQZ.h.

    {
      using std::abs;
      Index res = iu;
      while (res > 0)
      {
        Scalar s = abs(m_S.coeff(res-1,res-1)) + abs(m_S.coeff(res,res));
        if (s == Scalar(0.0))
          s = m_normOfS;
        if (abs(m_S.coeff(res,res-1)) < NumTraits<Scalar>::epsilon() * s)
          break;
        res--;
      }
      return res;
    }

template<typename MatrixType >

void Eigen::RealQZ< MatrixType >::hessenbergTriangular ( ) [private]

Reduces S and T to upper Hessenberg - triangular form

Definition at line 217 of file RealQZ.h.

    {

      const Index dim = m_S.cols();

      // perform QR decomposition of T, overwrite T with R, save Q
      HouseholderQR<MatrixType> qrT(m_T);
      m_T = qrT.matrixQR();
      m_T.template triangularView<StrictlyLower>().setZero();
      m_Q = qrT.householderQ();
      // overwrite S with Q* S
      m_S.applyOnTheLeft(m_Q.adjoint());
      // init Z as Identity
      if (m_computeQZ)
        m_Z = MatrixType::Identity(dim,dim);
      // reduce S to upper Hessenberg with Givens rotations
      for (Index j=0; j<=dim-3; j++) {
        for (Index i=dim-1; i>=j+2; i--) {
          JRs G;
          // kill S(i,j)
          if(m_S.coeff(i,j) != 0)
          {
            G.makeGivens(m_S.coeff(i-1,j), m_S.coeff(i,j), &m_S.coeffRef(i-1, j));
            m_S.coeffRef(i,j) = Scalar(0.0);
            m_S.rightCols(dim-j-1).applyOnTheLeft(i-1,i,G.adjoint());
            m_T.rightCols(dim-i+1).applyOnTheLeft(i-1,i,G.adjoint());
            // update Q
            if (m_computeQZ)
              m_Q.applyOnTheRight(i-1,i,G);
          }
          // kill T(i,i-1)
          if(m_T.coeff(i,i-1)!=Scalar(0))
          {
            G.makeGivens(m_T.coeff(i,i), m_T.coeff(i,i-1), &m_T.coeffRef(i,i));
            m_T.coeffRef(i,i-1) = Scalar(0.0);
            m_S.applyOnTheRight(i,i-1,G);
            m_T.topRows(i).applyOnTheRight(i,i-1,G);
            // update Z
            if (m_computeQZ)
              m_Z.applyOnTheLeft(i,i-1,G.adjoint());
          }
        }
      }
    }

template<typename _MatrixType>

ComputationInfo Eigen::RealQZ< _MatrixType >::info ( ) const [inline]

Reports whether previous computation was successful.

Returns:: Success if computation was succesful, NoConvergence otherwise.

Definition at line 166 of file RealQZ.h.

      {
        eigen_assert(m_isInitialized && "RealQZ is not initialized.");
        return m_info;
      }

template<typename _MatrixType>

Index Eigen::RealQZ< _MatrixType >::iterations ( ) const [inline]

Returns number of performed QR-like iterations.

Definition at line 174 of file RealQZ.h.

      {
        eigen_assert(m_isInitialized && "RealQZ is not initialized.");
        return m_global_iter;
      }

template<typename _MatrixType>

const MatrixType& Eigen::RealQZ< _MatrixType >::matrixQ ( ) const [inline]

Returns matrix Q in the QZ decomposition.

Returns:: A const reference to the matrix Q.

Definition at line 119 of file RealQZ.h.

                                        {
        eigen_assert(m_isInitialized && "RealQZ is not initialized.");
        eigen_assert(m_computeQZ && "The matrices Q and Z have not been computed during the QZ decomposition.");
        return m_Q;
      }

template<typename _MatrixType>

const MatrixType& Eigen::RealQZ< _MatrixType >::matrixS ( ) const [inline]

Returns matrix S in the QZ decomposition.

Returns:: A const reference to the matrix S.

Definition at line 139 of file RealQZ.h.

                                        {
        eigen_assert(m_isInitialized && "RealQZ is not initialized.");
        return m_S;
      }

template<typename _MatrixType>

const MatrixType& Eigen::RealQZ< _MatrixType >::matrixT ( ) const [inline]

Returns matrix S in the QZ decomposition.

Returns:: A const reference to the matrix S.

Definition at line 148 of file RealQZ.h.

                                        {
        eigen_assert(m_isInitialized && "RealQZ is not initialized.");
        return m_T;
      }

template<typename _MatrixType>

const MatrixType& Eigen::RealQZ< _MatrixType >::matrixZ ( ) const [inline]

Returns matrix Z in the QZ decomposition.

Returns:: A const reference to the matrix Z.

Definition at line 129 of file RealQZ.h.

                                        {
        eigen_assert(m_isInitialized && "RealQZ is not initialized.");
        eigen_assert(m_computeQZ && "The matrices Q and Z have not been computed during the QZ decomposition.");
        return m_Z;
      }

template<typename MatrixType >

void Eigen::RealQZ< MatrixType >::pushDownZero	(	Index	z,
		Index	f,
		Index	l
	)		`[inline, private]`

use zero in T(z,z) to zero S(l,l-1), working in block f..l

Definition at line 361 of file RealQZ.h.

    {
      JRs G;
      const Index dim = m_S.cols();
      for (Index zz=z; zz<l; zz++)
      {
        // push 0 down
        Index firstColS = zz>f ? (zz-1) : zz;
        G.makeGivens(m_T.coeff(zz, zz+1), m_T.coeff(zz+1, zz+1));
        m_S.rightCols(dim-firstColS).applyOnTheLeft(zz,zz+1,G.adjoint());
        m_T.rightCols(dim-zz).applyOnTheLeft(zz,zz+1,G.adjoint());
        m_T.coeffRef(zz+1,zz+1) = Scalar(0.0);
        // update Q
        if (m_computeQZ)
          m_Q.applyOnTheRight(zz,zz+1,G);
        // kill S(zz+1, zz-1)
        if (zz>f)
        {
          G.makeGivens(m_S.coeff(zz+1, zz), m_S.coeff(zz+1,zz-1));
          m_S.topRows(zz+2).applyOnTheRight(zz, zz-1,G);
          m_T.topRows(zz+1).applyOnTheRight(zz, zz-1,G);
          m_S.coeffRef(zz+1,zz-1) = Scalar(0.0);
          // update Z
          if (m_computeQZ)
            m_Z.applyOnTheLeft(zz,zz-1,G.adjoint());
        }
      }
      // finally kill S(l,l-1)
      G.makeGivens(m_S.coeff(l,l), m_S.coeff(l,l-1));
      m_S.applyOnTheRight(l,l-1,G);
      m_T.applyOnTheRight(l,l-1,G);
      m_S.coeffRef(l,l-1)=Scalar(0.0);
      // update Z
      if (m_computeQZ)
        m_Z.applyOnTheLeft(l,l-1,G.adjoint());
    }

template<typename _MatrixType>

RealQZ& Eigen::RealQZ< _MatrixType >::setMaxIterations ( Index maxIters ) [inline]

Sets the maximal number of iterations allowed to converge to one eigenvalue or decouple the problem.

Definition at line 183 of file RealQZ.h.

      {
        m_maxIters = maxIters;
        return *this;
      }

template<typename MatrixType >

void Eigen::RealQZ< MatrixType >::splitOffTwoRows ( Index i ) [inline, private]

decouple 2x2 diagonal block in rows i, i+1 if eigenvalues are real

Definition at line 311 of file RealQZ.h.

    {
      using std::abs;
      using std::sqrt;
      const Index dim=m_S.cols();
      if (abs(m_S.coeff(i+1,i))==Scalar(0))
        return;
      Index j = findSmallDiagEntry(i,i+1);
      if (j==i-1)
      {
        // block of (S T^{-1})
        Matrix2s STi = m_T.template block<2,2>(i,i).template triangularView<Upper>().
          template solve<OnTheRight>(m_S.template block<2,2>(i,i));
        Scalar p = Scalar(0.5)*(STi(0,0)-STi(1,1));
        Scalar q = p*p + STi(1,0)*STi(0,1);
        if (q>=0) {
          Scalar z = sqrt(q);
          // one QR-like iteration for ABi - lambda I
          // is enough - when we know exact eigenvalue in advance,
          // convergence is immediate
          JRs G;
          if (p>=0)
            G.makeGivens(p + z, STi(1,0));
          else
            G.makeGivens(p - z, STi(1,0));
          m_S.rightCols(dim-i).applyOnTheLeft(i,i+1,G.adjoint());
          m_T.rightCols(dim-i).applyOnTheLeft(i,i+1,G.adjoint());
          // update Q
          if (m_computeQZ)
            m_Q.applyOnTheRight(i,i+1,G);

          G.makeGivens(m_T.coeff(i+1,i+1), m_T.coeff(i+1,i));
          m_S.topRows(i+2).applyOnTheRight(i+1,i,G);
          m_T.topRows(i+2).applyOnTheRight(i+1,i,G);
          // update Z
          if (m_computeQZ)
            m_Z.applyOnTheLeft(i+1,i,G.adjoint());

          m_S.coeffRef(i+1,i) = Scalar(0.0);
          m_T.coeffRef(i+1,i) = Scalar(0.0);
        }
      }
      else
      {
        pushDownZero(j,i,i+1);
      }
    }

template<typename MatrixType >

void Eigen::RealQZ< MatrixType >::step	(	Index	f,
		Index	l,
		Index	iter
	)		`[inline, private]`

QR-like iterative step for block f..l

Definition at line 400 of file RealQZ.h.

    {
      using std::abs;
      const Index dim = m_S.cols();

      // x, y, z
      Scalar x, y, z;
      if (iter==10)
      {
        // Wilkinson ad hoc shift
        const Scalar
          a11=m_S.coeff(f+0,f+0), a12=m_S.coeff(f+0,f+1),
          a21=m_S.coeff(f+1,f+0), a22=m_S.coeff(f+1,f+1), a32=m_S.coeff(f+2,f+1),
          b12=m_T.coeff(f+0,f+1),
          b11i=Scalar(1.0)/m_T.coeff(f+0,f+0),
          b22i=Scalar(1.0)/m_T.coeff(f+1,f+1),
          a87=m_S.coeff(l-1,l-2),
          a98=m_S.coeff(l-0,l-1),
          b77i=Scalar(1.0)/m_T.coeff(l-2,l-2),
          b88i=Scalar(1.0)/m_T.coeff(l-1,l-1);
        Scalar ss = abs(a87*b77i) + abs(a98*b88i),
               lpl = Scalar(1.5)*ss,
               ll = ss*ss;
        x = ll + a11*a11*b11i*b11i - lpl*a11*b11i + a12*a21*b11i*b22i
          - a11*a21*b12*b11i*b11i*b22i;
        y = a11*a21*b11i*b11i - lpl*a21*b11i + a21*a22*b11i*b22i 
          - a21*a21*b12*b11i*b11i*b22i;
        z = a21*a32*b11i*b22i;
      }
      else if (iter==16)
      {
        // another exceptional shift
        x = m_S.coeff(f,f)/m_T.coeff(f,f)-m_S.coeff(l,l)/m_T.coeff(l,l) + m_S.coeff(l,l-1)*m_T.coeff(l-1,l) /
          (m_T.coeff(l-1,l-1)*m_T.coeff(l,l));
        y = m_S.coeff(f+1,f)/m_T.coeff(f,f);
        z = 0;
      }
      else if (iter>23 && !(iter%8))
      {
        // extremely exceptional shift
        x = internal::random<Scalar>(-1.0,1.0);
        y = internal::random<Scalar>(-1.0,1.0);
        z = internal::random<Scalar>(-1.0,1.0);
      }
      else
      {
        // Compute the shifts: (x,y,z,0...) = (AB^-1 - l1 I) (AB^-1 - l2 I) e1
        // where l1 and l2 are the eigenvalues of the 2x2 matrix C = U V^-1 where
        // U and V are 2x2 bottom right sub matrices of A and B. Thus:
        //  = AB^-1AB^-1 + l1 l2 I - (l1+l2)(AB^-1)
        //  = AB^-1AB^-1 + det(M) - tr(M)(AB^-1)
        // Since we are only interested in having x, y, z with a correct ratio, we have:
        const Scalar
          a11 = m_S.coeff(f,f),     a12 = m_S.coeff(f,f+1),
          a21 = m_S.coeff(f+1,f),   a22 = m_S.coeff(f+1,f+1),
                                    a32 = m_S.coeff(f+2,f+1),

          a88 = m_S.coeff(l-1,l-1), a89 = m_S.coeff(l-1,l),
          a98 = m_S.coeff(l,l-1),   a99 = m_S.coeff(l,l),

          b11 = m_T.coeff(f,f),     b12 = m_T.coeff(f,f+1),
                                    b22 = m_T.coeff(f+1,f+1),

          b88 = m_T.coeff(l-1,l-1), b89 = m_T.coeff(l-1,l),
                                    b99 = m_T.coeff(l,l);

        x = ( (a88/b88 - a11/b11)*(a99/b99 - a11/b11) - (a89/b99)*(a98/b88) + (a98/b88)*(b89/b99)*(a11/b11) ) * (b11/a21)
          + a12/b22 - (a11/b11)*(b12/b22);
        y = (a22/b22-a11/b11) - (a21/b11)*(b12/b22) - (a88/b88-a11/b11) - (a99/b99-a11/b11) + (a98/b88)*(b89/b99);
        z = a32/b22;
      }

      JRs G;

      for (Index k=f; k<=l-2; k++)
      {
        // variables for Householder reflections
        Vector2s essential2;
        Scalar tau, beta;

        Vector3s hr(x,y,z);

        // Q_k to annihilate S(k+1,k-1) and S(k+2,k-1)
        hr.makeHouseholderInPlace(tau, beta);
        essential2 = hr.template bottomRows<2>();
        Index fc=(std::max)(k-1,Index(0));  // first col to update
        m_S.template middleRows<3>(k).rightCols(dim-fc).applyHouseholderOnTheLeft(essential2, tau, m_workspace.data());
        m_T.template middleRows<3>(k).rightCols(dim-fc).applyHouseholderOnTheLeft(essential2, tau, m_workspace.data());
        if (m_computeQZ)
          m_Q.template middleCols<3>(k).applyHouseholderOnTheRight(essential2, tau, m_workspace.data());
        if (k>f)
          m_S.coeffRef(k+2,k-1) = m_S.coeffRef(k+1,k-1) = Scalar(0.0);

        // Z_{k1} to annihilate T(k+2,k+1) and T(k+2,k)
        hr << m_T.coeff(k+2,k+2),m_T.coeff(k+2,k),m_T.coeff(k+2,k+1);
        hr.makeHouseholderInPlace(tau, beta);
        essential2 = hr.template bottomRows<2>();
        {
          Index lr = (std::min)(k+4,dim); // last row to update
          Map<Matrix<Scalar,Dynamic,1> > tmp(m_workspace.data(),lr);
          // S
          tmp = m_S.template middleCols<2>(k).topRows(lr) * essential2;
          tmp += m_S.col(k+2).head(lr);
          m_S.col(k+2).head(lr) -= tau*tmp;
          m_S.template middleCols<2>(k).topRows(lr) -= (tau*tmp) * essential2.adjoint();
          // T
          tmp = m_T.template middleCols<2>(k).topRows(lr) * essential2;
          tmp += m_T.col(k+2).head(lr);
          m_T.col(k+2).head(lr) -= tau*tmp;
          m_T.template middleCols<2>(k).topRows(lr) -= (tau*tmp) * essential2.adjoint();
        }
        if (m_computeQZ)
        {
          // Z
          Map<Matrix<Scalar,1,Dynamic> > tmp(m_workspace.data(),dim);
          tmp = essential2.adjoint()*(m_Z.template middleRows<2>(k));
          tmp += m_Z.row(k+2);
          m_Z.row(k+2) -= tau*tmp;
          m_Z.template middleRows<2>(k) -= essential2 * (tau*tmp);
        }
        m_T.coeffRef(k+2,k) = m_T.coeffRef(k+2,k+1) = Scalar(0.0);

        // Z_{k2} to annihilate T(k+1,k)
        G.makeGivens(m_T.coeff(k+1,k+1), m_T.coeff(k+1,k));
        m_S.applyOnTheRight(k+1,k,G);
        m_T.applyOnTheRight(k+1,k,G);
        // update Z
        if (m_computeQZ)
          m_Z.applyOnTheLeft(k+1,k,G.adjoint());
        m_T.coeffRef(k+1,k) = Scalar(0.0);

        // update x,y,z
        x = m_S.coeff(k+1,k);
        y = m_S.coeff(k+2,k);
        if (k < l-2)
          z = m_S.coeff(k+3,k);
      } // loop over k

      // Q_{n-1} to annihilate y = S(l,l-2)
      G.makeGivens(x,y);
      m_S.applyOnTheLeft(l-1,l,G.adjoint());
      m_T.applyOnTheLeft(l-1,l,G.adjoint());
      if (m_computeQZ)
        m_Q.applyOnTheRight(l-1,l,G);
      m_S.coeffRef(l,l-2) = Scalar(0.0);

      // Z_{n-1} to annihilate T(l,l-1)
      G.makeGivens(m_T.coeff(l,l),m_T.coeff(l,l-1));
      m_S.applyOnTheRight(l,l-1,G);
      m_T.applyOnTheRight(l,l-1,G);
      if (m_computeQZ)
        m_Z.applyOnTheLeft(l,l-1,G.adjoint());
      m_T.coeffRef(l,l-1) = Scalar(0.0);
    }

Member Data Documentation

template<typename _MatrixType>

bool Eigen::RealQZ< _MatrixType >::m_computeQZ [private]

Definition at line 196 of file RealQZ.h.

template<typename _MatrixType>

Index Eigen::RealQZ< _MatrixType >::m_global_iter [private]

Definition at line 198 of file RealQZ.h.

template<typename _MatrixType>

ComputationInfo Eigen::RealQZ< _MatrixType >::m_info [private]

Definition at line 193 of file RealQZ.h.

template<typename _MatrixType>

bool Eigen::RealQZ< _MatrixType >::m_isInitialized [private]

Definition at line 195 of file RealQZ.h.

template<typename _MatrixType>

Index Eigen::RealQZ< _MatrixType >::m_maxIters [private]

Definition at line 194 of file RealQZ.h.

template<typename _MatrixType>

Scalar Eigen::RealQZ< _MatrixType >::m_normOfS [private]

Definition at line 197 of file RealQZ.h.

template<typename _MatrixType>

Scalar Eigen::RealQZ< _MatrixType >::m_normOfT [private]

Definition at line 197 of file RealQZ.h.

template<typename _MatrixType>

MatrixType Eigen::RealQZ< _MatrixType >::m_Q [private]

Definition at line 191 of file RealQZ.h.

template<typename _MatrixType>

MatrixType Eigen::RealQZ< _MatrixType >::m_S [private]

Definition at line 191 of file RealQZ.h.

template<typename _MatrixType>

MatrixType Eigen::RealQZ< _MatrixType >::m_T [private]

Definition at line 191 of file RealQZ.h.

template<typename _MatrixType>

Matrix<Scalar,Dynamic,1> Eigen::RealQZ< _MatrixType >::m_workspace [private]

Definition at line 192 of file RealQZ.h.

template<typename _MatrixType>

MatrixType Eigen::RealQZ< _MatrixType >::m_Z [private]

Definition at line 191 of file RealQZ.h.

The documentation for this class was generated from the following file:

RealQZ.h

Public Types

Public Member Functions

Private Types

Private Member Functions

Private Attributes

Detailed Description

template<typename _MatrixType> class Eigen::RealQZ< _MatrixType >

Member Typedef Documentation

Member Enumeration Documentation

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation

template<typename _MatrixType>
class Eigen::RealQZ< _MatrixType >