cgma
Public Member Functions | Static Public Member Functions | Private Attributes
TDDelaunay< TRIA, NODE > Class Template Reference

#include <TDDelaunay.hpp>

Inheritance diagram for TDDelaunay< TRIA, NODE >:
ToolData

List of all members.

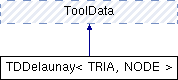
Public Member Functions

 TDDelaunay ()
virtual ~TDDelaunay ()
void reset ()
CubitVector & circumcenter2d (TRIA *tri_ptr)
double radius2d (TRIA *tri_ptr)
CubitVector & circumcenter (TRIA *tri_ptr)
double radius (TRIA *tri_ptr)
int circumsphere (TRIA *tet_ptr, CubitVector &center, double &rad)
int visit_flag ()
void visit_flag (int visit)
int tri_sort_list ()
void tri_sort_list (int index)

Static Public Member Functions

static int is_delaunay (const ToolData *td)

Private Attributes

CubitVector mCenter
double mRadius
int visitFlag
int sortIndex

Detailed Description

template<class TRIA, class NODE>
class TDDelaunay< TRIA, NODE >

Definition at line 18 of file TDDelaunay.hpp.

Constructor & Destructor Documentation

template<class TRIA , class NODE >
MY_INLINE TDDelaunay< TRIA, NODE >::TDDelaunay ( )

Definition at line 21 of file TDDelaunay.cpp.

{
  mRadius = -1.0;
  visitFlag = INT_MIN;
  sortIndex = -1;
}
template<class TRIA , class NODE >
MY_INLINE TDDelaunay< TRIA, NODE >::~TDDelaunay ( ) [virtual]

Definition at line 29 of file TDDelaunay.cpp.

{
}

Member Function Documentation

template<class TRIA , class NODE >
MY_INLINE CubitVector & TDDelaunay< TRIA, NODE >::circumcenter ( TRIA *  tri_ptr)

Definition at line 58 of file TDDelaunay.cpp.

{
  if (mRadius < 0.0) {

    NODE *corner[3];
    tri_ptr->tri_nodes( corner[0], corner[1], corner[2] );

      // Use coordinates relative to point `a' of the triangle. 
    CubitVector vec_ba(corner[0]->coordinates(), 
                       corner[1]->coordinates());
    CubitVector vec_ca(corner[0]->coordinates(), 
                       corner[2]->coordinates());

      // Squares of lengths of the edges incident to `a'. 
    double ba_length = vec_ba.length_squared();
    double ca_length = vec_ca.length_squared();
  
      // Cross product of these edges. 
      // (Take your chances with floating-point roundoff.)
    CubitVector cross_bc = vec_ba * vec_ca;

      // Calculate the denominator of the formulae. 
    double denominator = 0.5 / (cross_bc % cross_bc);
    assert(denominator != 0.0);

      // Calculate offset (from `a') of circumcenter. 
    mCenter  = (ba_length * vec_ca - ca_length * vec_ba) * cross_bc;
    mCenter *= denominator;

      // radius is length from point `a' to center
    mRadius = mCenter.length();

      // Add point `a' to get global coordinate of center
    mCenter += corner[0]->coordinates();
  }
  return mCenter;
}
template<class TRIA , class NODE >
MY_INLINE CubitVector & TDDelaunay< TRIA, NODE >::circumcenter2d ( TRIA *  tri_ptr)

Definition at line 103 of file TDDelaunay.cpp.

{
  if (mRadius < 0.0) {

    NODE *corner[3];
    tri_ptr->tri_nodes( corner[0], corner[1], corner[2] );

    double A11 = corner[1]->coordinates().x() - 
                 corner[0]->coordinates().x();
    double A12 = corner[1]->coordinates().y() - 
                 corner[0]->coordinates().y();
    double A21 = corner[2]->coordinates().x() - 
                 corner[0]->coordinates().x();
    double A22 = corner[2]->coordinates().y() - 
                 corner[0]->coordinates().y();
    double det = A11*A22 - A21*A12;
    if(det == 0.0)
    {
      PRINT_ERROR("Co-linear points can not be used to determine circle.\n");
      mCenter.x(0.0);//assert(0);
      mCenter.y(0.0);
      mCenter.z(0.0);
      return mCenter;
    }
    
    double B1 = (A11*A11) + (A12*A12);
    double B2 = (A21*A21) + (A22*A22);
    det += det;
    double xc = (B1*A22 - B2*A12)/det;
    double yc = (B2*A11 - B1*A21)/det;
    mRadius = xc * xc + yc * yc;
    mCenter.x( corner[0]->coordinates().x() + xc );
    mCenter.y( corner[0]->coordinates().y() + yc );
  }
  return mCenter;
}
template<class TRIA , class NODE >
MY_INLINE int TDDelaunay< TRIA, NODE >::circumsphere ( TRIA *  tet_ptr,
CubitVector &  center,
double &  rad 
)

Definition at line 179 of file TDDelaunay.cpp.

{
  if (mRadius != -1)
  {
    radsq = mRadius;
    center = mCenter;
    return CUBIT_SUCCESS;
  }
  double reltol = DBL_EPSILON * 100.0;

  NODE *na, *nb, *nc, *nd;
  tet_ptr->tet_nodes(nc, nb, na, nd);
  CubitVector a = na->coordinates();
  CubitVector b = nb->coordinates();
  CubitVector c = nc->coordinates();
  CubitVector d = nd->coordinates();

  CubitVector da = a - d;
  CubitVector db = b - d;
  CubitVector dc = c - d;

  double rhsa = 0.5*(SQR(da.x()) + SQR(da.y()) + SQR(da.z()));
  double rhsb = 0.5*(SQR(db.x()) + SQR(db.y()) + SQR(db.z()));
  double rhsc = 0.5*(SQR(dc.x()) + SQR(dc.y()) + SQR(dc.z()));

  double cpa = db.y()*dc.z() - dc.y()*db.z();
  double cpb = dc.y()*da.z() - da.y()*dc.z();
  double cpc = da.y()*db.z() - db.y()*da.z();

  double det = da.x()*cpa + db.x()*cpb + dc.x()*cpc;

  double xmax = CUBIT_MAX(fabs(a.x()),fabs(b.x()));
         xmax = CUBIT_MAX(xmax,fabs(c.x())); 
         xmax = CUBIT_MAX(xmax,fabs(d.x()));
  double ymax = CUBIT_MAX(fabs(a.y()),fabs(b.y()));
         ymax = CUBIT_MAX(ymax,fabs(c.y())); 
         ymax = CUBIT_MAX(ymax,fabs(d.y()));
  double zmax = CUBIT_MAX(fabs(a.z()),fabs(b.z()));
         zmax = CUBIT_MAX(zmax,fabs(c.z())); 
         zmax = CUBIT_MAX(zmax,fabs(d.z()));
  double tolabs = reltol*xmax*ymax*zmax;
  if (fabs(det) <= tolabs) {
    radsq = mRadius = -1.0; 
    return CUBIT_FAILURE;
  }
  center.x( (rhsa*cpa + rhsb*cpb + rhsc*cpc)/det );
  cpa = db.x()*rhsc - dc.x()*rhsb;
  cpb = dc.x()*rhsa - da.x()*rhsc;
  cpc = da.x()*rhsb - db.x()*rhsa;
  center.y( (da.z()*cpa + db.z()*cpb + dc.z()*cpc)/det );
  center.z( -(da.y()*cpa + db.y()*cpb + dc.y()*cpc)/det );
  radsq = SQR(center.x()) + SQR(center.y()) + SQR(center.z());
  center += d;

  mRadius = radsq;
  mCenter = center;

  return CUBIT_SUCCESS;
}
template<class TRIA, class NODE>
static int TDDelaunay< TRIA, NODE >::is_delaunay ( const ToolData *  td) [inline, static]

Definition at line 36 of file TDDelaunay.hpp.

     {return (CAST_TO(td, const TDDelaunay) != NULL);}
template<class TRIA , class NODE >
MY_INLINE double TDDelaunay< TRIA, NODE >::radius ( TRIA *  tri_ptr)

Definition at line 148 of file TDDelaunay.cpp.

{
  if (mRadius < 0.0) {
    this->circumcenter( tri_ptr );
  }
  return mRadius;
}
template<class TRIA , class NODE >
MY_INLINE double TDDelaunay< TRIA, NODE >::radius2d ( TRIA *  tri_ptr)

Definition at line 163 of file TDDelaunay.cpp.

{
  if (mRadius < 0.0) {
    this->circumcenter2d( tri_ptr );
  }
  return mRadius;
}
template<class TRIA , class NODE >
MY_INLINE void TDDelaunay< TRIA, NODE >::reset ( )

Definition at line 41 of file TDDelaunay.cpp.

{
  mRadius = -1.0;
  visitFlag = INT_MIN;
  sortIndex = -1;
}
template<class TRIA, class NODE>
int TDDelaunay< TRIA, NODE >::tri_sort_list ( ) [inline]

Definition at line 57 of file TDDelaunay.hpp.

{return sortIndex;};
template<class TRIA, class NODE>
void TDDelaunay< TRIA, NODE >::tri_sort_list ( int  index) [inline]

Definition at line 58 of file TDDelaunay.hpp.

{sortIndex = index;};
template<class TRIA, class NODE>
int TDDelaunay< TRIA, NODE >::visit_flag ( ) [inline]

Definition at line 53 of file TDDelaunay.hpp.

{return visitFlag;};
template<class TRIA, class NODE>
void TDDelaunay< TRIA, NODE >::visit_flag ( int  visit) [inline]

Definition at line 54 of file TDDelaunay.hpp.

{visitFlag = visit;};

Member Data Documentation

template<class TRIA, class NODE>
CubitVector TDDelaunay< TRIA, NODE >::mCenter [private]

Definition at line 25 of file TDDelaunay.hpp.

template<class TRIA, class NODE>
double TDDelaunay< TRIA, NODE >::mRadius [private]

Definition at line 26 of file TDDelaunay.hpp.

template<class TRIA, class NODE>
int TDDelaunay< TRIA, NODE >::sortIndex [private]

Definition at line 28 of file TDDelaunay.hpp.

template<class TRIA, class NODE>
int TDDelaunay< TRIA, NODE >::visitFlag [private]

Definition at line 27 of file TDDelaunay.hpp.

The documentation for this class was generated from the following files:
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Defines