|
cgma
|
|
cgma
|
#include <LoopParamTool.hpp>
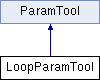
Definition at line 22 of file LoopParamTool.hpp.
Definition at line 34 of file LoopParamTool.cpp.
{
}
Definition at line 45 of file LoopParamTool.cpp.
{}
| CubitStatus LoopParamTool::check_selfintersecting_coincident_edges | ( | DLIList< DLIList< CubitPoint * > * > & | loop_cubit_points | ) | [private] |
Definition at line 554 of file LoopParamTool.cpp.
{
//This function checks each line segment against every other line segment
//to see if they intersect or overlap. Each line will be described
//by the following equations:
//
// Pa = P1 + ua( P2 - P1 )
// Pb = P3 + ub( P4 - P3 )
//
//Setting the Pa equal to Pb and solving for ua and ub you will get two
//equation. Both will have the common denominator:
//
// denom = ( (uv4.y() - uv3.y()) * (uv2.x() - uv1.x() ) -
// (uv4.x() - uv3.x()) * (uv2.y() - uv1.y() ) )
//
//And the numerators will be:
//
// numer_a = ( (uv4.x() - uv3.x()) * (uv1.y() - uv3.y() ) -
// (uv4.y() - uv3.y()) * (uv1.x() - uv3.x() ) )
//
// numer_b = ( (uv2.x() - uv1.x()) * (uv1.y() - uv3.y() ) -
// (uv2.y() - uv1.y()) * (uv1.x() - uv3.x() ) )
//
//ua and ub then become:
//
// ua = numer_a / denom
// ub = numer_b / denom
//
//If the lines are parallel then denom will be zero. If they are
//also coincedent then the numerators will also be zero. For the
//segments to intersect ua and ub need to both be between 0
//and 1.
int ii, jj, kk, ll;
for ( ii = 0; ii < loops_bounding_points.size(); ii++ )
{
DLIList<CubitPoint*>* sub_loops_bounding_points1 = loops_bounding_points.next(ii);
for( jj = 0; jj < sub_loops_bounding_points1->size(); jj++ )
{
CubitPoint* start_point1 = sub_loops_bounding_points1->next(jj);
CubitPoint* end_point1 = NULL;
if ( jj == sub_loops_bounding_points1->size()-1 )
end_point1 = sub_loops_bounding_points1->next(0);
else
end_point1 = sub_loops_bounding_points1->next(jj+1);
CubitVector uv1 = start_point1->coordinates();
CubitVector uv2 = end_point1->coordinates();
//Start with the current loop in the list. The previous
//lists have already been checked against this list.
for ( kk = ii; kk < loops_bounding_points.size(); kk++ )
{
DLIList<CubitPoint*>* sub_loops_bounding_points2 = loops_bounding_points.next(kk);
for ( ll = 0; ll < sub_loops_bounding_points2->size(); ll++ )
{
CubitPoint* start_point2 = sub_loops_bounding_points2->next(ll);
CubitPoint* end_point2 = NULL;
if ( ll == sub_loops_bounding_points2->size()-1 )
end_point2 = sub_loops_bounding_points2->next(0);
else
end_point2 = sub_loops_bounding_points2->next(ll+1);
CubitVector uv3 = start_point2->coordinates();
CubitVector uv4 = end_point2->coordinates();
if ( start_point1 == end_point2 || start_point1== start_point2 ||
end_point1 == start_point2 || end_point1 == end_point2 )
continue;
if ( (uv1 == uv3) && (uv2 == uv4) )
continue;
double denom = ( (uv4.y() - uv3.y()) * (uv2.x() - uv1.x() ) -
(uv4.x() - uv3.x()) * (uv2.y() - uv1.y() ) );
double numer_a = ( (uv4.x() - uv3.x()) * (uv1.y() - uv3.y() ) -
(uv4.y() - uv3.y()) * (uv1.x() - uv3.x() ) );
double numer_b = ( (uv2.x() - uv1.x()) * (uv1.y() - uv3.y() ) -
(uv2.y() - uv1.y()) * (uv1.x() - uv3.x() ) );
if( denom < CUBIT_RESABS && denom > -CUBIT_RESABS )
{
//The lines are parallel. Check the numerators to
//see if they are coincident.
if( numer_a < CUBIT_RESABS && numer_a > -CUBIT_RESABS &&
numer_b < CUBIT_RESABS && numer_b > -CUBIT_RESABS )
{
//The lines are coincident. Now see if the segments
//over lap.
double ua;
double ub;
if( (uv2.x() - uv1.x()) < CUBIT_RESABS &&
(uv2.x() - uv1.x()) > -CUBIT_RESABS )
{
if( (uv2.y() - uv1.y() < CUBIT_RESABS &&
uv2.y() - uv1.y() > -CUBIT_RESABS)){
PRINT_ERROR("Can't mesh due to zero-length edge.\n");
return CUBIT_FAILURE;
}
ua = (uv3.y() - uv1.y() ) / ( uv2.y() - uv1.y() );
ub = (uv4.y() - uv1.y() ) / ( uv2.y() - uv1.y() );
}
else
{
ua = (uv3.x() - uv1.x() ) / ( uv2.x() - uv1.x() );
ub = (uv4.x() - uv1.x() ) / ( uv2.x() - uv1.x() );
}
if ((ua > CUBIT_RESABS && ua < (1.0 - CUBIT_RESABS)) ||
(ub > CUBIT_RESABS && ub < (1.0 - CUBIT_RESABS)))
{
//The segments overlap.
PRINT_ERROR("Can't mesh due to coincident edges \n\n\n");
return CUBIT_FAILURE;
}
}
}
else
{
double ua = numer_a / denom;
double ub = numer_b / denom;
if( ( (ua > CUBIT_RESABS && ua < (1.0-CUBIT_RESABS)) &&
(ub > CUBIT_RESABS && ub < (1.0-CUBIT_RESABS))) )
{
PRINT_ERROR("Can't mesh due to self intersecting edges \n\n\n");
return CUBIT_FAILURE;
}
}
}//end of for ( ll )
}// end of for ( kk )
}//end of for ( jj )
}// end of for ( ii )
return CUBIT_SUCCESS;
}
| bool LoopParamTool::double_equal | ( | double | val, |
| double | equal_to | ||
| ) | [private] |
Transforms from the XY plane to the bestfit plane.
Definition at line 693 of file LoopParamTool.cpp.
{
if ( (val < (equal_to + CUBIT_RESABS)) && (val > (equal_to - CUBIT_RESABS)) )
return true;
else
return false;
}
| CubitStatus LoopParamTool::new_space_LoopParam | ( | DLIList< DLIList< CubitPoint * > * > & | loop_cubit_points, |
| CubitVector * | normal = NULL |
||
| ) |
This function is the function that changes the CubitPoints locations to the XY plane, and should be called only after calling new_space_LoopParam. Also, the original locations of the points are stored on a TDVector on each of the points. So to reverse the transformation, the calling code needs to get this ToolData off the CubitPoint, and reset its location based on the vector stored there. The calling code is reponsible for removing and deleting the memory of the TDVectors.
Definition at line 64 of file LoopParamTool.cpp.
{
int ii;
int jj;
double sumx = 0.0, sumy = 0.0, sumz = 0.0;
double sumxx = 0.0, sumxy = 0.0, sumxz = 0.0;
double sumyy = 0.0, sumyz = 0, sumzz = 0.0;
double aa[4][4];
double Xc = 0.0, Yc = 0.0, Zc = 0.0;
int n = 0;
CubitPoint *point, *point1, *point2;
CubitVector point_coordinates, point_coordinates1, point_coordinates2;
CubitVector cm_plane; // center of mass of a plane
CubitVector vec1, vec2, plane_normal;
DLIList<CubitPoint *> *sub_loops_cubit_points;
for ( ii = 0; ii < loops_cubit_points.size(); ii++ )
{
sub_loops_cubit_points = loops_cubit_points.get_and_step();
for ( jj = 0; jj < sub_loops_cubit_points->size(); jj++ )
{
point = sub_loops_cubit_points->get_and_step();
point_coordinates = point->coordinates();
sumx = sumx + point_coordinates.x();
sumy = sumy + point_coordinates.y();
sumz = sumz + point_coordinates.z();
sumxx = sumxx + ( point_coordinates.x() * point_coordinates.x() );
sumxy = sumxy + ( point_coordinates.x() * point_coordinates.y() );
sumxz = sumxz + ( point_coordinates.x() * point_coordinates.z() );
sumyy = sumyy + ( point_coordinates.y() * point_coordinates.y() );
sumyz = sumyz + ( point_coordinates.y() * point_coordinates.z() );
sumzz = sumzz + ( point_coordinates.z() * point_coordinates.z() );
n++;
}
}
Xc = sumx / n;
Yc = sumy / n;
Zc = sumz / n;
cm_plane.set(Xc,Yc,Zc);
if ( Xc < EPSILON_UPPER && Xc > EPSILON_LOWER ) Xc = 0.0;
if ( Yc < EPSILON_UPPER && Yc > EPSILON_LOWER ) Yc = 0.0;
if ( Zc < EPSILON_UPPER && Zc > EPSILON_LOWER ) Zc = 0.0;
aa[1][1] = sumxx - Xc * sumx;
aa[1][2] = sumxy - Yc * sumx;
aa[1][3] = sumxz - Zc * sumx;
aa[2][1] = sumxy - Xc * sumy;
aa[2][2] = sumyy - Yc * sumy;
aa[2][3] = sumyz - Zc * sumy;
aa[3][1] = sumxz - Xc * sumz;
aa[3][2] = sumyz - Yc * sumz;
aa[3][3] = sumzz - Zc * sumz;
for ( ii = 1; ii <=3; ii++ )
{
for ( jj = 1; jj <=3; jj++ )
if ( aa[ii][jj] < EPSILON_UPPER && aa[ii][jj] > EPSILON_LOWER )
aa[ii][jj] = 0.0;
}
double determinant_aa = aa[1][1] * ( aa[2][2]*aa[3][3] - aa[3][2]*aa[2][3] ) - aa[1][2] * ( aa[2][1]*aa[3][3] - aa[3][1]*aa[2][3] )
+ aa[1][3] * ( aa[2][1]*aa[3][2] - aa[3][1]*aa[2][2] );
if ( determinant_aa < EPSILON_UPPER && determinant_aa > EPSILON_LOWER )
determinant_aa = 0.0;
loops_cubit_points.reset();
// if determinant is 0.0 ( all the points are lying on the plane), the equation of a plane:
//(vec1) crossproduct (vec2)
// where vec1 and vec2 are the vectors originating from a common point( center of mass of a plane) and
// lying on the plane.
if(normal){
a = normal->x();
b = normal->y();
c = normal->z();
d = -(a*Xc + b*Yc + c*Zc );
}
else if ( determinant_aa == 0.0 )
{
sub_loops_cubit_points = loops_cubit_points.get_and_step();
point1 = sub_loops_cubit_points->get_and_step();
point2 = sub_loops_cubit_points->get_and_step();
point_coordinates1 = point1->coordinates();
point_coordinates2 = point2->coordinates();
vec1 = cm_plane - point_coordinates1;
vec2 = cm_plane - point_coordinates2;
plane_normal = vec1 * vec2;
a = plane_normal.x();
b = plane_normal.y();
c = plane_normal.z();
d = -( a*Xc + b*Yc + c*Zc );
}
else // to calculate eigen vector corresponding to the smallest eigen value
{
// to calculate the inverse of a matrix
int i, j, k;
int icol = -1, irow = -1, l, ll;
double big, z, pivinv, temp;
int indxc[4];
int indxr[4];
int ipiv[4];
for ( j = 1; j <= 3; j++)
{
indxc[j] = 0;
indxr[j] = 0;
ipiv[j] = 0;
}
for ( i = 1; i <= 3;i++)
{
big = 0.0;
for ( j = 1; j <= 3; j++)
{
if ( ipiv[j] != 1 )
{
for ( k = 1; k <= 3; k++)
{
if (ipiv[k] == 0 )
{
if (fabs(aa[j][k]) >= big )
{
big = fabs(aa[j][k]);
irow = j;
icol = k;
}
}
else if(ipiv[k]>1) PRINT_ERROR("Matrix is singular1\n");
}
}
}
ipiv[icol]+=1;
if ( irow != icol )
{
for (l=1; l <= 3;l++)
SWAP( aa[irow][l],aa[icol][l] );
}
indxr[i] = irow;
indxc[i] = icol;
if(aa[icol][icol] == 0.0 ) PRINT_ERROR("Matrix is singular2\n");
pivinv = 1.0/aa[icol][icol];
aa[icol][icol] = 1.0;
for( l = 1; l <= 3; l++)
aa[icol][l] *= pivinv;
for ( ll = 1; ll <= 3; ll++)
{
if ( ll != icol )
{
z = aa[ll][icol];
aa[ll][icol] = 0.0;
for ( l = 1;l <= 3; l++)
aa[ll][l] -= aa[icol][l] * z;
}
}
for ( l = 3; l >= 1; l-- )
{
if ( indxr[l] != indxc[l] )
for ( k = 1; k <= 3; k++ )
SWAP( aa[k][indxr[l]], aa[k][indxc[l]] )
}
}
// Power Method to get the Eigen Vector corresponding to the smallest Eigen value
double x[4] = {0.0, 1.0, 1.1, 1.2};
double dd[4];
double zz[4];
int t = 0;
double diff1 = 0.0, diff2 = 0.0;
int flag;
double largest_dd;
while ( t <= 100 )
{
flag = 1;
for ( i = 1; i <= 3; i++ )
{
dd[i] = 0.0;
for ( j = 1; j <= 3; j++ )
{
dd[i] = dd[i] + aa[i][j] * x[j];
if (dd[i] > EPSILON_LOWER && dd[i] < EPSILON_UPPER) dd[i] = 0.0;
}
}
t = t+1;
largest_dd = dd[1] > dd[2] ? ( dd[1] > dd[3] ? dd[1] : dd[3] ) : ( dd[2] > dd[3] ? dd[2] : dd[3] );
for ( i = 1; i <= 3; i++ )
{
zz[i] = dd[i]/largest_dd;
if (zz[i] > EPSILON_LOWER && zz[i] < EPSILON_UPPER) zz[i] = 0.0;
}
for ( i = 1; i <= 3; i++ )
{
diff1 = fabs(x[i] - zz[i]);
diff2 = fabs(diff1) - EPSILON_UPPER*fabs(zz[i]);
if ( diff2 <= 0.0 )
continue;
else
{
flag = 0;
break;
}
}
if ( flag == 1 )
break;
if (flag == 0 )
{
for ( i = 1; i <= 3; i++ )
x[i] = zz[i];
}
}
for ( i = 1; i <= 3; i++ )
{
x[i] = zz[i];
if ( (x[i] < EPSILON_UPPER) && (x[i] > EPSILON_LOWER) )
x[i] = 0.0;
}
a = x[1];
b = x[2];
c = x[3];
d = -(a*Xc+b*Yc+c*Zc);
}
//printf("\n\nEquation of Plane is %fx+%fy+%fz+%f = 0\n",a,b,c,d);
loops_cubit_points.reset();
sub_loops_cubit_points = loops_cubit_points.get_and_step();
CubitPoint *p1 = sub_loops_cubit_points->get_and_step();
CubitVector p1_coordinates = p1->coordinates();
double p1x = p1_coordinates.x() - (p1_coordinates.x()*a + p1_coordinates.y()*b + p1_coordinates.z()*c + d)*
(a)/(pow(a,2)+pow(b,2)+pow(c,2));
double p1y = p1_coordinates.y() - (p1_coordinates.x()*a + p1_coordinates.y()*b + p1_coordinates.z()*c + d)*
(b)/(pow(a,2)+pow(b,2)+pow(c,2));
double p1z = p1_coordinates.z() - (p1_coordinates.x()*a + p1_coordinates.y()*b + p1_coordinates.z()*c + d)*
(c)/(pow(a,2)+pow(b,2)+pow(c,2));
p1_coordinates.set(p1x, p1y, p1z);
CubitVector surf_normal;
surf_normal.x(a); surf_normal.y(b); surf_normal.z(-1.0);
surf_normal.normalize();
// use the first two points on the boundary to define gradient vectors
// and orient our uv space.
CubitPoint *p2;
CubitVector p2_coordinates;
double p2x, p2y, p2z;
double cos = 1.0;
//
while (cos == 1.0)
{
p2 = sub_loops_cubit_points->get_and_step();
p2_coordinates = p2->coordinates();
p2x = p2_coordinates.x() - (p2_coordinates.x()*a + p2_coordinates.y()*b + p2_coordinates.z()*c + d)*
(a)/(pow(a,2)+pow(b,2)+pow(c,2));
p2y = p2_coordinates.y() - (p2_coordinates.x()*a + p2_coordinates.y()*b + p2_coordinates.z()*c + d)*
(b)/(pow(a,2)+pow(b,2)+pow(c,2));
p2z = p2_coordinates.z() - (p2_coordinates.x()*a + p2_coordinates.y()*b + p2_coordinates.z()*c + d)*
(c)/(pow(a,2)+pow(b,2)+pow(c,2));
p2_coordinates.set(p2x, p2y, p2z);
if ( p1_coordinates == p2_coordinates )
cos = 1.0;
else cos = 0.0;
}
Du = p2_coordinates - p1_coordinates;
Du.normalize();
Dv = surf_normal * Du;
Dv.normalize();
uvCenter = p1_coordinates;
sub_loops_cubit_points->reset();
return CUBIT_SUCCESS;
}
| CubitStatus LoopParamTool::set_up_space | ( | void | ) | [virtual] |
Definition at line 53 of file LoopParamTool.cpp.
{
return CUBIT_SUCCESS;
}
| CubitStatus LoopParamTool::transform_loopspoints_to_uv | ( | DLIList< DLIList< CubitPoint * > * > & | points | ) |
Definition at line 473 of file LoopParamTool.cpp.
{
int ii, jj;
CubitStatus ret_value = CUBIT_SUCCESS;
DLIList<CubitPoint *> *sub_loops_point_list;
CubitPoint *point_ptr;
CubitVector xyz_location, uv_location, point_coordinates;
// transform the points on the best fit plane
ret_value = transform_to_bestfit_plane( loops_point_list);
/*printf("\n after transform to best fit plane\n");
for( ii = 0; ii < loops_point_list.size(); ii++)
{
sub_loops_point_list = loops_point_list.get_and_step();
for ( jj = 0; jj < sub_loops_point_list->size(); jj++)
{
point_ptr = sub_loops_point_list->get_and_step();
point_coordinates = point_ptr->coordinates();
printf(" %f %f %f \n",point_coordinates.x(),point_coordinates.y(),point_coordinates.z());
}
}*/
//transform to u-v
for ( ii = 0; ii < loops_point_list.size(); ii++)
{
sub_loops_point_list = loops_point_list.get_and_step();
for ( jj = 0; jj < sub_loops_point_list->size(); jj++ )
{
point_ptr = sub_loops_point_list->get_and_step();
xyz_location = point_ptr->coordinates();
ret_value = transform_to_uv_local( xyz_location, uv_location );
point_ptr->set(uv_location);
}
}
if ( check_selfintersecting_coincident_edges(loops_point_list) != CUBIT_SUCCESS )
{
//PRINT_ERROR("Self interesections in parameter space found.\n");
ret_value = CUBIT_FAILURE;
}
else
ret_value = CUBIT_SUCCESS;
// if the self-intersecting and coincident edges are not there then return CUBIT_SUCCESS
// else restore the points to their original positions and return CUBIT_FAILURE
return ret_value;
//don't do the rest for now...
if ( ret_value == CUBIT_SUCCESS )
return CUBIT_SUCCESS;
else
{
ToolData *td;
for ( ii = 0; ii < loops_point_list.size(); ii++ )
{
sub_loops_point_list = loops_point_list.next(ii);
for ( jj = 0; jj < sub_loops_point_list->size(); jj++)
{
point_ptr = sub_loops_point_list->next(jj);
td = point_ptr->get_TD(&TDVector::is_td_vector);
TDVector *td_pos = CAST_TO(td, TDVector);
CubitVector orig_xyz_location = td_pos->get_vector();
point_ptr->set(orig_xyz_location);
point_coordinates = point_ptr->coordinates();
}
}
return CUBIT_FAILURE;
}
}
| CubitStatus LoopParamTool::transform_to_bestfit_plane | ( | DLIList< DLIList< CubitPoint * > * > & | loop_cubit_points | ) | [private] |
Checks to see if the tranformation of the points caused self intersections. Returns CUBIT_FAILURE if there are any found.
Definition at line 350 of file LoopParamTool.cpp.
{
int ii, jj;
DLIList<CubitPoint *> *sub_loop_cubit_points = NULL;
CubitPoint *point_ptr = NULL;
CubitVector point_coordinates;
double x, y, z;
for ( ii = 0; ii < loop_cubit_points.size(); ii++ )
{
sub_loop_cubit_points = loop_cubit_points.get_and_step();
for ( jj = 0; jj < sub_loop_cubit_points->size(); jj++ )
{
point_ptr = sub_loop_cubit_points->get_and_step();
ToolData* td = point_ptr->get_TD( &TDVector::is_td_vector );
TDVector* td_pos = NULL;
if( NULL == td )
td_pos = new TDVector(point_ptr->coordinates());
else
td_pos = static_cast<TDVector*>( td );
point_ptr->add_TD(td_pos);
point_coordinates = point_ptr->coordinates();
x = point_coordinates.x() - (point_coordinates.x()*a + point_coordinates.y()*b + point_coordinates.z()*c + d)*
(a)/(pow(a,2)+pow(b,2)+pow(c,2));
y = point_coordinates.y() - (point_coordinates.x()*a + point_coordinates.y()*b + point_coordinates.z()*c + d)*
(b)/(pow(a,2)+pow(b,2)+pow(c,2));
z = point_coordinates.z() - (point_coordinates.x()*a + point_coordinates.y()*b + point_coordinates.z()*c + d)*
(c)/(pow(a,2)+pow(b,2)+pow(c,2));
point_coordinates.set(x, y, z);
point_ptr->set(point_coordinates);
}
}
return CUBIT_SUCCESS;
}
| CubitStatus LoopParamTool::transform_to_uv | ( | const CubitVector & | , |
| CubitVector & | |||
| ) | [virtual] |
Implements ParamTool.
Definition at line 397 of file LoopParamTool.cpp.
{
PRINT_ERROR("This function is not appropriate for the the LoopParamTool.\n");
assert(0);
return CUBIT_FAILURE;
}
| CubitStatus LoopParamTool::transform_to_uv_local | ( | CubitVector & | xyz_location, |
| CubitVector & | uv_location | ||
| ) | [private] |
Transforms the points to a least-squares-fit plane. Creates and stores the original locations on TDVectors that are added to the CubitPoints.
Definition at line 411 of file LoopParamTool.cpp.
{
// Translate to local origin at center
CubitVector vect = xyz_location - uvCenter;
// Multiply by transpose (inverse) of transformation vector
uv_location.x( vect % Du );
uv_location.y( vect % Dv );
uv_location.z( 1.0 );
return CUBIT_SUCCESS;
}
| CubitStatus LoopParamTool::transform_to_xyz | ( | CubitVector & | , |
| const CubitVector & | |||
| ) | [virtual] |
Implements ParamTool.
Definition at line 431 of file LoopParamTool.cpp.
{
PRINT_ERROR("This function is not appropriate for the the LoopParamTool.\n");
assert(0);
return CUBIT_FAILURE;
}
| CubitStatus LoopParamTool::transform_to_xyz_local | ( | CubitVector & | xyz_location, |
| CubitVector & | uv_location | ||
| ) | [private] |
Transforms the vector to the xy plane.
Definition at line 444 of file LoopParamTool.cpp.
{
// Multiply by transformation matrix
CubitVector vect;
vect.x( uv_location.x() * Du.x() +
uv_location.y() * Dv.x() );
vect.y( uv_location.x() * Du.y() +
uv_location.y() * Dv.y() );
vect.z( uv_location.x() * Du.z() +
uv_location.y() * Dv.z() );
// Translate from origin
xyz_location = vect + uvCenter;
return CUBIT_SUCCESS;
}
double LoopParamTool::a [private] |
Definition at line 62 of file LoopParamTool.hpp.
double LoopParamTool::b [private] |
Definition at line 62 of file LoopParamTool.hpp.
double LoopParamTool::c [private] |
Definition at line 62 of file LoopParamTool.hpp.
double LoopParamTool::d [private] |
Definition at line 62 of file LoopParamTool.hpp.
CubitVector LoopParamTool::Du [private] |
This function must be called first for this tool. This sets up the plane and the transformation to the XY plane.
Definition at line 59 of file LoopParamTool.hpp.
CubitVector LoopParamTool::Dv [private] |
Definition at line 60 of file LoopParamTool.hpp.
CubitVector LoopParamTool::uvCenter [private] |
Definition at line 61 of file LoopParamTool.hpp.